Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T06:16:10.394Z Has data issue: false hasContentIssue false
  • English
  • Français

Finite-dimensional approximations for Nica–Pimsner algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  09 August 2019

EVGENIOS T. A. KAKARIADIS
EVGENIOS T. A. KAKARIADIS*
Affiliation:
School of Mathematics, Statistics and Physics, Newcastle University, Newcastle upon Tyne, NE1 7RU, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give necessary and sufficient conditions for nuclearity of Cuntz–Nica–Pimsner algebras for a variety of quasi-lattice ordered groups. First we deal with the free abelian lattice case. We use this as a stepping-stone to tackle product systems over quasi-lattices that are controlled by the free abelian lattice and satisfy a minimality property. Our setting accommodates examples like the Baumslag–Solitar lattice for 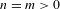$n=m>0$ and the right-angled Artin groups. More generally, the class of quasi-lattices for which our results apply is closed under taking semi-direct and graph products. In the process we accomplish more. Our arguments tackle Nica–Pimsner algebras that admit a faithful conditional expectation on a small fixed point algebra and a faithful copy of the coefficient algebra. This is the case for CNP-relative quotients in-between the Toeplitz–Nica–Pimsner algebra and the Cuntz–Nica–Pimsner algebra. We complete this study with the relevant results on exactness.

Keywords

C*-correspondencesproduct systemsNica–Pimsner algebrasexactnessnuclearity

MSC classification

Primary: 46L08: $C^*$-modules 46L05: General theory of $C^*$-algebras
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 12 , December 2020 , pp. 3375 - 3402
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albandik, S. and Meyer, R.. Product systems over Ore monoids. Doc. Math. 20 (2015), 1331–1402.Google Scholar
Arveson, W.. Continuous analogues of Fock space. Mem. Amer. Math. Soc. 80(409) (1989).Google Scholar
Brown, N. and Ozawa, N.. C∗ -algebras and Finite Dimensional Approximations (Graduate Studies in Mathematics, 88). American Mathematical Society, Providence, RI, 2008.Google Scholar
Carlsen, T. M., Larsen, N. S., Sims, A. and Vittadello, S. T.. Co-universal algebras associated to product systems, and gauge-invariant uniqueness theorems. Proc. Lond. Math. Soc. (3) 103 (2011), 563–600.Google Scholar
Crisp, J. and Laca, M.. On the Toeplitz algebras of right-angled and finite-type Artin groups. J. Aust. Math. Soc. 72 (2002), 223–245.Google Scholar
Crisp, J. and Laca, M.. Boundary quotients of Toeplitz algebras of right-angled Artin groups. J. Funct. Anal. 242 (2007), 125–156.Google Scholar
Deaconu, V.. Iterating the Pimsner construction. New York J. Math. 13 (2007), 199–213.Google Scholar
Dor-On, A. and Kakariadis, E. T. A.. Operator algebras for higher rank analysis. Preprint, 2018,arXiv:1803.11260. J. Anal. Math. to appear.Google Scholar
Dor-On, A. and Katsoulis, E. G.. Tensor algebras of product systems and their C*-envelopes. Preprint, 2018, arXiv:1801.07296.Google Scholar
Fletcher, J.. Iterating the Cuntz–Nica–Pimsner construction for compactly aligned product systems. New York J. Math. 24 (2018), 739–814.Google Scholar
Fowler, N. J.. Discrete product systems of Hilbert bimodules. Pacific J. Math. 204 (2002), 335–375.Google Scholar
Green, E. R.. Graph products of groups. PhD Thesis, University of Leeds, 1990.Google Scholar
Kakariadis, E. T. A.. A note on the gauge invariant uniqueness theorem for C*-correspondences. Israel J. Math. 215 (2016), 513–521.Google Scholar
Kakariadis, E. T. A.. On Nica–Pimsner algebras of C*-dynamical systems over ℤ+n. Int. Math. Res. Not. IMRN 4 (2017), 1013–1065.Google Scholar
Kakariadis, E. T. A. and Peters, J. R.. Representations of C*-dynamical systems implemented by Cuntz families. Münster J. Math. 6 (2013), 383–411.Google Scholar
Katsura, T.. On C*-algebras associated with C*-correspondences. J. Funct. Anal. 217 (2004), 366–401.Google Scholar
Kumjian, A. and Pask, D.. Higher rank graph C*-algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Kumjian, A., Pask, D. and Sims, A.. On twisted higher-rank graph C*-algebras. Trans. Amer. Math. Soc. 367 (2015), 5177–5216.Google Scholar
Kwaśniewski, B. K. and Larsen, N. S.. Nica–Toeplitz algebras associated with right tensor C*-precategories over right LCM semigroups: Part I Uniqueness results. Preprint, 2016, arXiv:1611.08525v1.Google Scholar
Lance, E. C.. Hilbert C*-modules. A Toolkit for Operator Algebraists (London Mathematical Society Lecture Note Series, 210). Cambridge University Press, Cambridge, 1995.Google Scholar
Li, X.. Nuclearity of semigroup C*-algebras and the connection to amenability. Adv. Math. 244 (2013), 626–662.Google Scholar
Muhly, P. S. and Solel, B.. Tensor algebras over C*-correspondences: representations, dilations and C*-envelopes. J. Funct. Anal. 158 (1998), 389–457.Google Scholar
Nica, A.. C*-algebras generated by isometries and Wiener–Hopf operators. J. Operator Theory 27 (1992), 17–52.Google Scholar
Pimsner, M. V.. A Class of C*-algebras Generalizing both Cuntz–Krieger Algebras and Crossed Products by ℤ (Fields Institute Communications, 12). American Mathematical Society, Providence, RI, 1997, pp. 189–212.Google Scholar
Rennie, A., Robertson, D. and Sims, A.. Groupoid Fell bundles for product systems over quasi-lattice ordered groups. Math. Proc. Cambridge Philos. Soc. 163 (2017), 561–580.Google Scholar
Sehnem, C. F.. On C*-algebras associated to product systems. Preprint, 2018, arXiv:1804.10546.Google Scholar
Sims, A. and Yeend, T.. Cuntz–Nica–Pimsner algebras associated to product systems of Hilbert bimodules. J. Operator Theory 64 (2010), 349–376.Google Scholar
Spielberg, J.. C*-algebras for categories of paths associated to the Baumslag–Solitar groups. J. Lond. Math. Soc. (2) 86 (2012), 728–754.Google Scholar