Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T23:55:20.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions with shrinking fibers

Part of: Dynamical systems with hyperbolic behavior Ergodic theory

Published online by Cambridge University Press:  24 April 2020

BENOÎT R. KLOECKNER Open the ORCID record for BENOÎT R. KLOECKNER [Opens in a new window]
BENOÎT R. KLOECKNER*
Affiliation:
LAMA, Univ. Paris-Est Créteil, Univ. Gustave Eiffel, UPEM, CNRS, F-94010, Créteil, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider dynamical systems 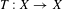$T:X\rightarrow X$ that are extensions of a factor 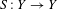$S:Y\rightarrow Y$ through a projection 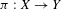$\unicode[STIX]{x1D70B}:X\rightarrow Y$ with shrinking fibers, that is, such that $T$ is uniformly continuous along fibers 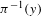$\unicode[STIX]{x1D70B}^{-1}(y)$ and the diameter of iterate images of fibers 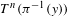$T^{n}(\unicode[STIX]{x1D70B}^{-1}(y))$ uniformly go to zero as 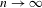$n\rightarrow \infty$. 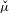We prove that every $S$-invariant measure $\check{\unicode[STIX]{x1D707}}$ has a unique $T$-invariant lift $\unicode[STIX]{x1D707}$, and prove that many properties of 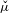$\check{\unicode[STIX]{x1D707}}$ lift to $\unicode[STIX]{x1D707}$: ergodicity, weak and strong mixing, decay of correlations and statistical properties (possibly with weakening in the rates). The basic tool is a variation of the Wasserstein distance, obtained by constraining the optimal transportation paradigm to displacements along the fibers. We extend classical arguments to a general setting, enabling us to translate potentials and observables back and forth between 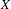$X$ and $Y$.

Keywords

classical ergodic theorysmooth dynamicstopological dynamics

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states
Secondary: 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.) 37A25: Ergodicity, mixing, rates of mixing 37A30: Ergodic theorems, spectral theory, Markov operators 37A35: Entropy and other invariants, isomorphism, classification
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 6 , June 2021 , pp. 1795 - 1834
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, J. F., Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140(2) (2000), 351–398.CrossRefGoogle Scholar
Alves, J. F., Dias, C. L., Luzzatto, S. and Pinheiro, V.. SRB measures for partially hyperbolic systems whose central direction is weakly expanding. J. Eur. Math. Soc. (JEMS) 19(10) (2017), 2911–2946.CrossRefGoogle Scholar
Araújo, V., Galatolo, S. and Pacifico, M. J.. Decay of correlations for maps with uniformly contracting fibers and logarithm law for singular hyperbolic attractors. Math. Z. 276(3–4) (2014), 1001–1048.CrossRefGoogle Scholar
Avila, A., Gouëzel, S. and Yoccoz, J.-C.. Exponential mixing for the Teichmüller flow. Publ. Math. Inst. Hautes Études Sci. 104 (2006), 143–211.CrossRefGoogle Scholar
Alves, J. F.. SRB measures for partially hyperbolic attractors, 2015, http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.709.4072&rep=rep1&type=pdf.Google Scholar
Araújo, V., Melbourne, I. and Varandas, P.. Rapid mixing for the Lorenz attractor and statistical limit laws for their time-1 maps. Comm. Math. Phys. 340(3) (2015), 901–938.CrossRefGoogle Scholar
Araujo, V., Pacifico, M. J., Pujals, E. R. and Viana, M.. Singular-hyperbolic attractors are chaotic. Trans. Amer. Math. Soc. 361(5) (2009), 2431–2485.CrossRefGoogle Scholar
Abdenur, F. and Viana, M.. Flavors of partial hyperbolicity, 2009, http://w3.impa.br/∼viana/out/flavors.pdf.Google Scholar
Butterley, O. and Melbourne, I.. Disintegration of invariant measures for hyperbolic skew products. Israel J. Math. 219(1) (2017), 171–188.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) , revised edn. Springer, Berlin, 2008. With a preface by David Ruelle, edited by Jean-René Chazottes.CrossRefGoogle Scholar
Cuny, C., Dedecker, J., Korepanov, A. and Merlevède, F.. Rates in almost sure invariance principle for slowly mixing dynamical systems. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2019.2. Published online 26 February 2019.CrossRefGoogle Scholar
Catsigeras, E. and Enrich, H.. SRB-like measures for C 0 dynamics. Bull. Pol. Acad. Sci. Math. 59(2) (2011), 151–164.CrossRefGoogle Scholar
Castro, A. and Nascimento, T.. Statistical properties of the maximal entropy measure for partially hyperbolic attractors. Ergod. Th. & Dynam. Sys. 37(4) (2017), 1060–1101.CrossRefGoogle Scholar
Crovisier, S. and Potrie, R.. Introduction to partially hyperbolic dynamics. Lecture Notes for School on Dynamical Systems (ICTP, Trieste), 3, 2015.Google Scholar
Climenhaga, V., Pesin, Y. and Zelerowicz, A.. Equilibrium states in dynamical systems via geometric measure theory. Bull. Amer. Math. Soc. 56 (2019), 569–610.CrossRefGoogle Scholar
Campbell, J. T. and Quas, A. N.. A generic C 1 expanding map has a singular S-R-B measure. Comm. Math. Phys. 221(2) (2001), 335–349.CrossRefGoogle Scholar
Castro, A. and Varandas, P.. Equilibrium states for non-uniformly expanding maps: decay of correlations and strong stability. Ann. Inst. H. Poincaré Anal. Non Linéaire 30(2) (2013), 225–249.CrossRefGoogle Scholar
Díaz, L. J., Horita, V., Rios, I. and Sambarino, M.. Destroying horseshoes via heterodimensional cycles: generating bifurcations inside homoclinic classes. Ergod. Th. & Dynam. Sys. 29(2) (2009), 433–474.CrossRefGoogle Scholar
A., Fan and Jiang, Y.. On Ruelle–Perron–Frobenius operators. I. Ruelle theorem. Comm. Math. Phys. 223(1) (2001), 125–141.Google Scholar
A., Fan and Jiang, Y.. On Ruelle–Perron–Frobenius operators. II. Convergence speeds. Comm. Math. Phys. 223(1) (2001), 143–159.Google Scholar
Galatolo, S.. Quantitative statistical stability and speed of convergence to equilibrium for partially hyperbolic skew products. J. Éc. Polytech. Math. 5 (2018), 377–405.CrossRefGoogle Scholar
Galatolo, S. and Lucena, R.. Spectral gap and quantitative statistical stability for systems with contracting fibers and Lorenz like maps. Discrete Contin. Dyn. Syst. 40(3) (2020), 1309–1360.CrossRefGoogle Scholar
Galatolo, S., Nisoli, I. and Pacifico, M. J.. Decay of correlations, quantitative recurrence and logarithm law for contracting Lorenz attractors. J. Stat. Phys. 170(5) (2018), 862–882.CrossRefGoogle Scholar
Gouëzel, S.. Almost sure invariance principle for dynamical systems by spectral methods. Ann. Probab. 38(4) (2010), 1639–1671.CrossRefGoogle Scholar
Galatolo, S. and Pacifico, M. J.. Lorenz-like flows: exponential decay of correlations for the Poincaré map, logarithm law, quantitative recurrence. Ergod. Th. & Dynam. Sys. 30(6) (2010), 1703–1737.CrossRefGoogle Scholar
Guihéneuf, P.-A.. Dynamical properties of spatial discretizations of a generic homeomorphism. Ergod. Th. & Dynam. Sys. 35(5) (2015), 1474–1523.CrossRefGoogle Scholar
Kloeckner, B.. An optimal transportation approach to the decay of correlations for non-uniformly expanding maps. Ergod. Th. & Dynam. Sys. 40(3) (2020), 714–750.CrossRefGoogle Scholar
Kuratowski, K. and Ryll-Nardzewski, C.. A general theorem on selectors. Bull. Acad. Pol. Sci. Sér. Sci. Math. Astronom. Phys. 13 (1965), 397–403.Google Scholar
Ledrappier, F.. Principe variationnel et systèmes dynamiques symboliques. Z. Wahrsch. Verw. Gebiete 30(3) (1974), 185–202.CrossRefGoogle Scholar
Ledrappier, F.. Propriétés ergodiques des mesures de Sinai. Publ. Math. Inst. Hautes Études Sci. 59(1) (1984), 163–188.CrossRefGoogle Scholar
Leplaideur, R., Oliveira, K. and Rios, I.. Equilibrium states for partially hyperbolic horseshoes. Ergod. Th. & Dynam. Sys. 31(1) (2011), 179–195.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16(3) (1977), 568–576.CrossRefGoogle Scholar
Melbourne, I. and Nicol, M.. Almost sure invariance principle for nonuniformly hyperbolic systems. Comm. Math. Phys. 260(1) (2005), 131–146.CrossRefGoogle Scholar
Melbourne, I. and Török, A.. Central limit theorems and invariance principles for time-one maps of hyperbolic flows. Comm. Math. Phys. 229(1) (2002), 57–71.CrossRefGoogle Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Trans. 1952(71) (1952), 55.Google Scholar
Ramos, V. and Siqueira, J.. On equilibrium states for partially hyperbolic horseshoes: uniqueness and statistical properties. Bull. Braz. Math. Soc. (N.S.) 48(3) (2017), 347–375.CrossRefGoogle Scholar
Simmons, D.. Conditional measures and conditional expectation; Rohlin’s disintegration theorem. Discrete Contin. Dyn. Syst. 32(7) (2012), 2565–2582.CrossRefGoogle Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73 (1967), 747–817.CrossRefGoogle Scholar
Thaler, M.. Estimates of the invariant densities of endomorphisms with indifferent fixed points. Israel J. Math. 37(4) (1980), 303–314.CrossRefGoogle Scholar
Tyran-Kamińska, M.. An invariance principle for maps with polynomial decay of correlations. Comm. Math. Phys. 260(1) (2005), 1–15.CrossRefGoogle Scholar
Villani, C.. Optimal Transport (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 338) . Springer, Berlin, 2009. .CrossRefGoogle Scholar
Walters, P.. Ruelle’s operator theorem and g-measures. Trans. Amer. Math. Soc. 214 (1975), 375–387.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.CrossRefGoogle Scholar
Young, L.-S.. Statistical properties of dynamical systems with some hyperbolicity. Ann. of Math. (2) 147(3) (1998), 585–650.CrossRefGoogle Scholar
Young, L.-S.. What are SRB measures, and which dynamical systems have them? J. Stat. Phys. 108(5–6) (2002), 733–754.CrossRefGoogle Scholar