Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T12:38:59.001Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansive homeomorphisms and hyperbolic diffeomorphisms on 3-manifolds

Published online by Cambridge University Press:  19 September 2008

José L. Vieitez
José L. Vieitez
Affiliation:
Inst. de Matemática, Fac. de Ingenieria, Universidad de la República, Montevideo, Uruguay
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is a contribution to the classification problem of expansive homeomorphisms. Let M be a compact connected oriented three dimensional topological manifold without boundary and f: M → M an expansive homeomorphism.We show that if the topologically hyperbolic period points of f are dense in M then M = 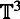, and f is conjugate to an Anosov diffeomorphism. This follows from our basic result: for such a homeomorphism, all stable and unstable sets are (tamely embedded) topological manifolds.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 3 , June 1996 , pp. 591 - 622
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[B]Bing, R. H.. The Geometric Topology of 3-Manifolds. Amer. Math. Soc. Coll. Pub., vol. 40 (1983).Google Scholar
[D-H]Duvall, P. F. and Husch, L. S.. Analysis on topological manifolds. Fund. Math. LXXVD (1972), 75–90.CrossRefGoogle Scholar
[Fa]Falconer, K. J.. The Geometry of Fractal Sets. Cambridge University Press, Cambridge, 1985.CrossRefGoogle Scholar
[Fr]Franks, J.. Anosov diffeomorphisms. Global Analysis Proc. Symp. Pure Math 14. Amer. Math. Soc., pp. 61–93 (1970).CrossRefGoogle Scholar
[F-R]Franks, J. and Robinson, R. C.. A quasi-Anosov diffeomorphism that is not Anosov. Trans. Amer. Math. Soc. 233 (1976), 267–278.CrossRefGoogle Scholar
[H1]Hiraide, K.. Expansive homeomorphisms with the pseudo-orbit tracing property of n-tori. J. Math. Soc. Japan 41 (3) (1989), 357–389.Google Scholar
[H2]Hiraide, K.. Expansive homeomorphisms of compact surfaces are pseudo-Anosov. Osaka J. Math. 27 (1990), 117–162.Google Scholar
[H-H]Hector, G. and Hirsch, U.. Introduction to the Geometry of Foliations, Part B, Foliations of Codimension One, Aspects of Mathematics, Vol E3. Vieweg, 1983.CrossRefGoogle Scholar
[H-W]Hurewicz, W. and Wallman, H.. Dimension Theory (Princeton Math. Series 4). Princeton University Press, 1948.Google Scholar
[K]Kuratowski, K.. Topology. Academic, New York-London, 1966.Google Scholar
[L1]Lewowicz, J.. Persistence in expansive systems. Ergod. Th. & Dynam. Sys. 3 (1983), 567–578.CrossRefGoogle Scholar
[L2]Lewowicz, J.. Expansive homeomorphisms of surfaces. Bol. Soc. Bras. Mat. 20 (1) (1989), 113–133.CrossRefGoogle Scholar
[M]Moise, E. E.. Geometric Topology in Dimensions 2 and 3. Springer, New York, 1977.CrossRefGoogle Scholar
[R]Roussarie, R.. Sur les Feuilletages des Variéetés de dimension trois. Ann. Inst. Fourier, Grenoble 21 (3) (1971), 13–82.CrossRefGoogle Scholar
[S]Spanier, E. H.. Algebraic Topology. McGraw-Hill, New York, 1965.Google Scholar
[V1]Vieitez, J. L.. Three Dimensional Expansive Homeomorphisms, Dynamical Systems. Santiago de Chile 1990, Pitman Series, Harlow, 1993.Google Scholar
[V2]Vieitez, J. L.. Funciones de Liapunov Hiperbó1icas. Publicaciones Matem. del Uruguay. 27–35Google Scholar
[W]Wilder, R. L.. Topology of Manifolds. AMS, Providence, RI, 1976.Google Scholar