Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T13:55:38.467Z Has data issue: false hasContentIssue false
  • English
  • Français

Examples of distorted interval diffeomorphisms of intermediate regularity

Part of: Low-dimensional dynamical systems Smooth dynamical systems: general theory Special aspects of infinite or finite groups

Published online by Cambridge University Press:  08 September 2021

LEONARDO DINAMARCA  and
MAXIMILIANO ESCAYOLA
LEONARDO DINAMARCA*
Affiliation:
Departamento de Matemática y Ciencias de la Computación, Universidad de Santiago de Chile (USACH), Alameda Libertador Bernardo O’Higgins 3363, Estación Central, Santiago, Chile (e-mail: [email protected])
MAXIMILIANO ESCAYOLA
Affiliation:
Departamento de Matemática y Ciencias de la Computación, Universidad de Santiago de Chile (USACH), Alameda Libertador Bernardo O’Higgins 3363, Estación Central, Santiago, Chile (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We improve a recent construction of Andrés Navas to produce the first examples of 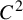$C^2$ -undistorted diffeomorphisms of the interval that are 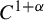$C^{1+\alpha }$ -distorted (for every ${\alpha < 1}$ ). We do this via explicit computations due to the failure of an extension to class 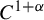$C^{1+\alpha }$ of a classical lemma related to the work of Nancy Kopell.

Keywords

interval diffeomorphismHölder continuitydistorted elementdistortion

MSC classification

Primary: 20F99: None of the above, but in this section 37C05: Smooth mappings and diffeomorphisms 37C85: Dynamics of group actions other than ${bf Z}$ and ${bf R}$, and foliations 37E05: Maps of the interval (piecewise continuous, continuous, smooth)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 11 , November 2022 , pp. 3311 - 3324
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bonatti, C. and Farinelli, É.. Centralizers of ${C}^1$ -contractions of the half line. Groups Geom. Dyn. 9(3) (2015), 831–889.CrossRefGoogle Scholar
Castro, G., Jorquera, E. and Navas, A.. Sharp regularity for certain nilpotent group actions on the interval. Math. Ann. 359(1–2) (2014), 101–152.CrossRefGoogle Scholar
Deroin, B., Kleptsyn, V. and Navas, A.. Sur la dynamique unidimensionnelle en régularité intermédiaire. Acta Math. 199(2) (2007), 199–262.CrossRefGoogle Scholar
Druck, S. and Firmo, S.. Periodic leaves for diffeomorphisms preserving codimension one foliations. J. Math. Soc. Japan 55(1) (2003), 13–37.CrossRefGoogle Scholar
Eynard-Bontemps, H. and Navas, A.. Mather invariant, conjugates, and distortion for diffeomorphisms of the interval. J. Funct. Analysis 281(9) (2021), 109–149.CrossRefGoogle Scholar
Gromov, M.. Asymptotic invariants of infinite groups. Geometric Group Theory (Sussex, 1991) (London Mathematical Society Lecture Notes Series, 182). Vol. 2. Cambridge University Press, Cambridge, 1993, pp. 1–295.Google Scholar
Kim, S. H. and Koberda, T.. Diffeomorphism groups of critical regularity. Invent. Math. 221(2) (2020), 421–501.CrossRefGoogle Scholar
Kleptsyn, V. and Navas, A.. A Denjoy type theorem for commuting circle diffeomorphisms with derivatives having different Hölder differentiability classes. Mosc. Math. J. 8(3) (2008), 477–492.CrossRefGoogle Scholar
Kopell, N.. Commuting diffeomorphisms. Global Analysis (Berkeley, CA, 1968) (Proceedings of Symposia in Pure Mathematics, XIV). American Mathematical Society, Providence, RI, 1970, pp. 165–184.Google Scholar
Mann, K. and Wolff, M.. Reconstructing maps out of groups. Ann. Sci. Éc. Norm. Supér. (4), to appear.Google Scholar
Navas, A.. Groups of Circle Diffeomorphisms (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, IL, 2011.CrossRefGoogle Scholar
Navas, A.. On centralizers of interval diffeomorphisms in critical (intermediate) regularity. J. Anal. Math. 121 (2013), 1–30.CrossRefGoogle Scholar
Navas, A.. On conjugates and the asymptotic distortion of 1-dimensional ${C}^{1+\mathrm{bv}}$ diffeomorphisms. Preprint, 2021, arXiv:1811.06077.CrossRefGoogle Scholar
Navas, A.. (Un)distorted diffeomorphisms in different regularities. Israel J. Math., doi: 10.1007/s11856-021-2188-z. Published online 21 August 2021.CrossRefGoogle Scholar
Pixton, D.. Nonsmoothable, unstable group actions. Trans. Amer. Math. Soc. 229 (1977), 259–268.CrossRefGoogle Scholar
Rosendal, C.. Coarse Geometry of Topological Groups. Unpublished book.Google Scholar
Tsuboi, T.. Homological and dynamical study on certain groups of Lipschitz homeomorphisms of the circle. J. Math. Soc. Japan 47 (1995), 1–30.CrossRefGoogle Scholar