Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-30T20:08:47.804Z Has data issue: false hasContentIssue false
  • English
  • Français

The error term in the prime orbit theorem for expanding semiflows

Published online by Cambridge University Press:  24 January 2017

MASATO TSUJII
MASATO TSUJII*
Affiliation:
Department of Mathematics, Kyushu University, Motooka 744, Nishi-ku, Fukuoka, 819-0395, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider suspension semiflows of angle-multiplying maps on the circle and study the distributions of periods of their periodic orbits. Under generic conditions on the roof function, we give an asymptotic formula on the number 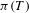$\unicode[STIX]{x1D70B}(T)$ of prime periodic orbits with period 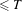$\leq T$. The error term is bounded, at least, by

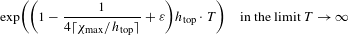$$\begin{eqnarray}\exp \biggl(\biggl(1-\frac{1}{4\lceil \unicode[STIX]{x1D712}_{\text{max}}/h_{\text{top}}\rceil }+\unicode[STIX]{x1D700}\biggr)h_{\text{top}}\cdot T\biggr)\quad \text{in the limit }T\rightarrow \infty\end{eqnarray}$$
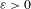for arbitrarily small $\unicode[STIX]{x1D700}>0$, where 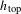$h_{\text{top}}$ and 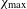$\unicode[STIX]{x1D712}_{\text{max}}$ are, respectively, the topological entropy and the maximal Lyapunov exponent of the semiflow.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1954 - 2000
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baladi, V. and Tsujii, M.. Dynamical determinants and spectrum for hyperbolic diffeomorphisms. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469) . American Mathematical Society, Providence, RI, 2008, pp. 29–68.CrossRefGoogle Scholar
Buser, P.. Geometry and Spectra of Compact Riemann Surfaces (Progress in Mathematics, 106) . Birkhäuser, Boston, MA, 1992.Google Scholar
Giulietti, P., Liverani, C. and Pollicott, M.. Anosov flows and dynamical zeta functions. Ann. of Math. (2) 178(2) (2013), 687–773.CrossRefGoogle Scholar
Gohberg, I., Goldberg, S. and Krupnik, N.. Traces and Determinants of Linear Operators (Operator Theory: Advances and Applications, 116) . Birkhäuser, Basel, 2000.CrossRefGoogle Scholar
Hunt, B. R., Sauer, T. and Yorke, J. A.. Prevalence: a translation-invariant ‘almost every’ on infinite-dimensional spaces. Bull. Amer. Math. Soc. (N.S.) 27(2) (1992), 217–238.CrossRefGoogle Scholar
Hunt, B. R., Sauer, T. and Yorke, J. A.. Prevalence. An addendum to: “Prevalence: a translation-invariant ‘almost every’ on infinite-dimensional spaces”. Bull. Amer. Math. Soc. (N.S.) 27(2) (1992), 217–238; Bull. Amer. Math. Soc. (N.S.), 28 (2) (1993), 306–307.CrossRefGoogle Scholar
Lu, Z.-H.. Topological pressure of continuous flows without fixed points. J. Math. Anal. Appl. 311(2) (2005), 703–714.CrossRefGoogle Scholar
Luo, W. Z. and Sarnak, P.. Quantum ergodicity of eigenfunctions on PSL2(Z)\H 2 . Publ. Math. Inst. Hautes Études Sci. 81 (1995), 207–237.CrossRefGoogle Scholar
Mañé, R.. Ergodic Theory and Differentiable Dynamics: Results in Mathematics and Related Areas (3) (Ergebnisse der Mathematik und ihrer Grenzgebiete (3), 8) . Springer, Berlin, 1987, translated from the Portuguese by Silvio Levy.CrossRefGoogle Scholar
Ott, W. and Yorke, J. A.. Prevalence. Bull. Amer. Math. Soc. (N.S.) 42(3) (2005), 263–290 (electronic).CrossRefGoogle Scholar
Parry, W. and Pollicott, M.. An analogue of the prime number theorem for closed orbits of Axiom A flows. Ann. of Math. (2) 118(3) (1983), 573–591.CrossRefGoogle Scholar
Pollicott, M.. On the mixing of Axiom A attracting flows and a conjecture of Ruelle. Ergod. Th. & Dynam. Sys. 19(2) (1999), 535–548.CrossRefGoogle Scholar
Pollicott, M. and Sharp, R.. Exponential error terms for growth functions on negatively curved surfaces. Amer. J. Math. 120(5) (1998), 1019–1042.CrossRefGoogle Scholar
Ruelle, D.. Locating resonances for Axiom A dynamical systems. J. Stat. Phys. 44(3–4) (1986), 281–292.CrossRefGoogle Scholar
Stoyanov, L.. Spectra of Ruelle transfer operators for axiom A flows. Nonlinearity 24(4) (2011), 1089–1120.CrossRefGoogle Scholar
Triebel, H.. Theory of Function Spaces (Monographs in Mathematics, 78) . Birkhäuser, Basel, 1983.CrossRefGoogle Scholar
Tsujii, M.. A measure on the space of smooth mappings and dynamical system theory. J. Math. Soc. Japan 44(3) (1992), 415–425.CrossRefGoogle Scholar
Tsujii, M.. Decay of correlations in suspension semi-flows of angle-multiplying maps. Ergod. Th. & Dynam. Sys. 28(1) (2008), 291–317.CrossRefGoogle Scholar
Tsujii, M.. Quasi-compactness of transfer operators for contact Anosov flows. Nonlinearity 23(7) (2010), 1495–1545.CrossRefGoogle Scholar
Tsujii, M.. Contact Anosov flows and the Fourier–Bros–Iagolnitzer transform. Ergod. Th. & Dynam. Sys. 32(6) (2012), 2083–2118.CrossRefGoogle Scholar