Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T04:27:15.506Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic properties of the Anzai skew-product for the non-commutative torus

Part of: Ergodic theory Infinite-dimensional manifolds Selfadjoint operator algebras Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  14 January 2020

SIMONE DEL VECCHIO Open the ORCID record for SIMONE DEL VECCHIO [Opens in a new window] ,
FRANCESCO FIDALEO Open the ORCID record for FRANCESCO FIDALEO [Opens in a new window] ,
LUCA GIORGETTI Open the ORCID record for LUCA GIORGETTI [Opens in a new window]  and
STEFANO ROSSI Open the ORCID record for STEFANO ROSSI [Opens in a new window]
SIMONE DEL VECCHIO
Affiliation:
Dipartimento di Matematica, Università di Roma Tor Vergata, Via della Ricerca Scientifica 1, Roma00133, Italy email [email protected], [email protected], [email protected]
FRANCESCO FIDALEO
Affiliation:
Dipartimento di Matematica, Università di Roma Tor Vergata, Via della Ricerca Scientifica 1, Roma00133, Italy email [email protected], [email protected], [email protected]
LUCA GIORGETTI
Affiliation:
Department of Mathematics, Vanderbilt University, 1326 Stevenson Center, Nashville, TN37240, USA email [email protected]
STEFANO ROSSI
Affiliation:
Dipartimento di Matematica, Università di Roma Tor Vergata, Via della Ricerca Scientifica 1, Roma00133, Italy email [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide a systematic study of a non-commutative extension of the classical Anzai skew-product for the cartesian product of two copies of the unit circle to the non-commutative 2-tori. In particular, some relevant ergodic properties are proved for these quantum dynamical systems, extending the corresponding ones enjoyed by the classical Anzai skew-product. As an application, for a uniquely ergodic Anzai skew-product 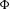$\unicode[STIX]{x1D6F7}$ on the non-commutative $2$-torus 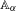$\mathbb{A}_{\unicode[STIX]{x1D6FC}}$, 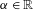$\unicode[STIX]{x1D6FC}\in \mathbb{R}$, we investigate the pointwise limit, 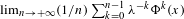$\lim _{n\rightarrow +\infty }(1/n)\sum _{k=0}^{n-1}\unicode[STIX]{x1D706}^{-k}\unicode[STIX]{x1D6F7}^{k}(x)$, for 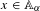$x\in \mathbb{A}_{\unicode[STIX]{x1D6FC}}$ and $\unicode[STIX]{x1D706}$ a point in the unit circle, and show that there are examples for which the limit does not exist, even in the weak topology.

Keywords

operator algebrasnon-commutative torusskew-productergodic dynamical systemsunique ergodicity

MSC classification

Primary: 46L55: Noncommutative dynamical systems 58J51: Relations between spectral theory and ergodic theory, e.g. quantum unique ergodicity
Secondary: 37A55: Relations with the theory of $C^*$-algebras 58B34: Noncommutative geometry (à la Connes) 46L65: Quantizations, deformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 4 , April 2021 , pp. 1064 - 1085
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abadie, B. and Dykema, K.. Unique ergodicity of free shifts and some other automorphisms of C ∗ -algebras. J. Operator Theory 61 (2009), 279–294.Google Scholar
Anzai, H.. Ergodic Anzai skew-product transformations on the torus. Osaka Math. J. 3 (1951), 83–99.Google Scholar
Barreto, S. D. and Fidaleo, F.. Disordered Fermions on lattices and their spectral properties. J. Stat. Phys. 143 (2011), 657–684.CrossRefGoogle Scholar
Boca, F.-P. Rotation C ∗ -Algebras and almost Mathieu Operators. Theta, Bucharest, 2001.Google Scholar
Carey, A., Phillips, J. and Rennie, A.. Spectral triples: examples and index theory. Noncommutative Geometry and Physics: Renormalisation, Motives, Index Theory (ESI Lectures in Mathematics and Physics) . Ed. Carey, A.. European Mathematical Society, Zurich, 2011, pp. 175–265.10.4171/008-1/5CrossRefGoogle Scholar
Connes, A.. Noncommutative Geometry. Academic Press, San Diego. CA, 1994.Google Scholar
Connes, A. and Moscovici, H.. Modular curvature for noncommutative two-tori. J. Amer. Math. Soc. 27 (2014), 639–684.CrossRefGoogle Scholar
Cornfeld, I. P., Fomin, S. V. and Sinai, Ya G.. Ergodic Theory. Springer, Berlin, 1982.CrossRefGoogle Scholar
Crismale, V. and Fidaleo, F.. De Finetti theorem on the CAR algebra. Commun. Math. Phys. 315 (2012), 135–152.CrossRefGoogle Scholar
Crismale, V. and Fidaleo, F.. Exchangeable stochastic processes and symmetric states in quantum probability. Ann. Mat. Pura Appl. (4) 194 (2015), 969–993.CrossRefGoogle Scholar
Davidson, K. R.. C ∗ -Algebras by Example (Fields Institute Monographs, 6) . American Mathematical Society, Providence, RI, 1996.CrossRefGoogle Scholar
Fidaleo, F.. KMS states and the chemical potential for disordered systems. Commun. Math. Phys. 262 (2006), 373–391.CrossRefGoogle Scholar
Fidaleo, F.. On the entangled ergodic theorem. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 10 (2007), 67–77.CrossRefGoogle Scholar
Fidaleo, F.. On strong ergodic properties of quantum dynamical systems. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 12 (2009), 551–564.CrossRefGoogle Scholar
Fidaleo, F.. The entangled ergodic theorem in the almost periodic case. Linear Algebra Appl. 432 (2010), 526–535.CrossRefGoogle Scholar
Fidaleo, F.. Nonconventional ergodic theorems for quantum dynamical systems. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 17 (2014), 1450009.10.1142/S021902571450009XCrossRefGoogle Scholar
Fidaleo, F.. Uniform convergence of Cesaro averages for uniquely ergodic C ∗ -dynamical systems. Entropy 20 (2018), 987.CrossRefGoogle Scholar
Fidaleo, F.. Fourier analysis for type III representations of the noncommutative torus. J. Fourier Anal. Appl. 25 (2019), 2801–2835.CrossRefGoogle Scholar
Fidaleo, F. and Mukhamedov, F.. Strict weak mixing of some C ∗ -dynamical systems based on free shifts. J. Math. Anal. Appl. 336 (2007), 180–187.CrossRefGoogle Scholar
Fidaleo, F. and Mukhamedov, F.. Ergodic properties of Bogoliubov automorphisms in free probability. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 13 (2010), 393–411.CrossRefGoogle Scholar
Fidaleo, F. and Suriano, L.. Type III representations and modular spectral triples for the noncommutative torus. J. Funct. Anal. 275(2018) 1484–1531.CrossRefGoogle Scholar
Furstenberg, H.. Strict ergodicity and transformation on the torus. Amer. J. Math. 83(1961) 573–601.CrossRefGoogle Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31(1977) 204–256.CrossRefGoogle Scholar
Longo, R. and Peligrad, C.. Noncommutative topological dynamics and compact actions on C ∗ -algebras. J. Funct. Anal. 58(1984) 157–174.CrossRefGoogle Scholar
Niculescu, C. P., Ströh, A. and Zsidó, L.. Noncommutative extensions of classical and multiple recurrence theorems. J. Operator Theory 50 (2003), 3–52.Google Scholar
Osaka, H. and Phillips, N. C.. Furstenberg transformations on irrational rotation algebras. Ergod. Th. & Dynam. Sys. 26 (2006), 1623–1651.CrossRefGoogle Scholar
Rieffel, M. A.. The cancellation theorem for projective modules over irrational rotation C ∗ -algebras. Proc. Lond. Math. Soc. 47 (1983), 285–302.CrossRefGoogle Scholar
Robinson, E. A. Jr. On uniform convergence in the Wiener–Wintner theorem. J. Lond. Math. Soc. 49 (1994), 493–501.CrossRefGoogle Scholar
Sakai, S.. C ∗ -Algebras and W ∗ -Algebras. Springer, Berlin, 1971.Google Scholar