Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T09:54:13.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic properties of bimodal circle maps

Published online by Cambridge University Press:  27 November 2017

SYLVAIN CROVISIER ,
PABLO GUARINO  and
LIVIANA PALMISANO
SYLVAIN CROVISIER
Affiliation:
CNRS - Université Paris-Sud, Laboratoire de Mathématiques d’Orsay, France email [email protected]
PABLO GUARINO
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Brazil email [email protected]
LIVIANA PALMISANO
Affiliation:
IMPAN, Institute of Mathematics, Polish Academy of Sciences, Warsaw, Poland email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give conditions that characterize the existence of an absolutely continuous invariant probability measure for a degree one 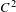$C^{2}$ endomorphism of the circle which is bimodal, such that all its periodic orbits are repelling, and such that both boundaries of its rotation interval are irrational numbers. Those conditions are satisfied when the boundary points of the rotation interval belong to a Diophantine class. In particular, they hold for Lebesgue almost every rotation interval. By standard results, the measure obtained is a global physical measure and it is hyperbolic.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 6 , June 2019 , pp. 1462 - 1500
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnol’d, V. I.. Small denominators I. Mappings of the circle onto itself. Izv. Akad. Nauk. Math. Ser. 25 (1961), 21–86: Trans. Amer. Math. Soc. Ser. 2, 46, (1965), 213–284.Google Scholar
Avila, A., Lyubich, M. and de Melo, W.. Regular or stochastic dynamics in real analytic families of unimodal maps. Invent. Math. 154 (2003), 451–550.Google Scholar
Benedicks, M. and Carleson, L.. On iterations of 1 - ax 2 on (-1, 1). Ann. of Math. (2) 122 (1985), 1–25.Google Scholar
Bowen, R.. Invariant measures for Markov maps of the interval. Commun. Math. Phys. 69 (1979), 1–17.Google Scholar
Boyland, P.. Bifurcations of circle maps: Arnol’d tongues, bistability and rotation intervals. Commun. Math. Phys. 106 (1986), 353–381.Google Scholar
Bruin, H.. The existence of absolutely continuous invariant measures is not a topological invariant for unimodal maps. Ergod. Th. & Dynam. Sys. 18(3) (1998), 555–565.Google Scholar
Bruin, H., Rivera-Letelier, J., Shen, W. and van Strien, S.. Large derivatives, backward contraction and invariant densities for interval maps. Invent. Math. 172 (2008), 509–533.Google Scholar
Chenciner, A., Gambaudo, J.-M. and Tresser, C.. Une remarque sur la structure des endomorphismes de degré 1 du cercle. C. R. Acad. Sci. Paris, Sér. I 299 (1984), 145–148.Google Scholar
Collet, P. and Eckmann, J.-P.. Positive Lyapunov exponents and absolutely continuity for maps of the interval. Ergod. Th. & Dynam. Sys. 3 (1983), 13–46.Google Scholar
Crovisier, S.. Nombre de rotation et dynamique faiblement hyperbolique. PhD Thesis, Laboratoire de Mathématiques d’Orsay, CNRS – Université Paris-Sud, 2001.Google Scholar
Graczyk, J.. Dynamics of circle maps with flat spots. Fund. Math. 209 (2010), 267–290.Google Scholar
Graczyk, J., Sands, D. and Świa̧tek, G.. La dérivée schwarzienne en dynamique unimodale. C. R. Acad. Sci. Paris, Sér. I 332 (2001), 329–332.Google Scholar
Graczyk, J., Sands, D. and Świa̧tek, G.. Metric attractors for smooth unimodal maps. Ann. of Math. (2) 159 (2004), 725–740.Google Scholar
Herman, M.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–233.Google Scholar
Jakobson, M.. Absolutely continuous invariant measures for one-parameter families of one-dimensional maps. Commun. Math. Phys. 81 (1981), 39–88.Google Scholar
Kozlovski, O., Shen, W. and van Strien, S.. Density of hyperbolicity in dimension one. Ann. of Math. (2) 166 (2007), 145–182.Google Scholar
Ledrappier, F.. Some properties of absolutely continuous invariant measures on an interval. Ergod. Th. & Dynam. Sys. 1 (1981), 77–93.Google Scholar
Lyubich, M.. Almost every real quadratic map is either regular or stochastic. Ann. of Math. (2) 156 (2002), 1–78.Google Scholar
Lyubich, M. and Milnor, J.. The Fibonacci unimodal map. J. Amer. Math. Soc. 6 (1993), 425–457.Google Scholar
Mañé, R.. Hyperbolicity, sinks and measure in one-dimensional dynamics. Commun. Math. Phys. 100 (1985), 495–524. See also Erratum, Commun. Math. Phys. 112 (1987), 721–724.Google Scholar
Martens, M. and Nowicki, T.. Invariant measures for typical quadratic maps. Astérisque 261 (2000), 239–252.Google Scholar
May, R. M.. Simple mathematical models with very complicated dynamics. Nature 261 (1976), 459–467.Google Scholar
de Melo, W. and van Strien, S.. One-dimensional Dynamics. Springer, New York, 1993.Google Scholar
Misiurewicz, M.. Rotation intervals for a class of maps of the real line into itself. Ergod. Th. & Dynam. Sys. 6 (1986), 117–132.Google Scholar
Nowicki, T. and van Strien, S.. Invariant measures exist under a summability condition for unimodal maps. Invent. Math. 105 (1991), 123–136.Google Scholar
Świa̧tek, G.. Endpoints of rotation intervals for maps of the circle. Ergod. Th. & Dynam. Sys. 9 (1989), 173–190.Google Scholar
Triestino, M.. Généricité au sens probabiliste dans les difféomorphismes du cercle. Ensaios Matemáticos 27 (2014), 1–98.Google Scholar