Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T04:30:23.030Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic currents dual to a real tree

Published online by Cambridge University Press:  12 November 2014

THIERRY COULBOIS  and
ARNAUD HILION
THIERRY COULBOIS
Affiliation:
Mathématiques, Université d’Aix-Marseille, Marseille, France email [email protected], [email protected]
ARNAUD HILION
Affiliation:
Mathématiques, Université d’Aix-Marseille, Marseille, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

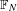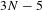Let $T$ be an $\mathbb{R}$-tree with dense orbits in the boundary of outer space. When the free group $\mathbb{F}_{N}$ acts freely on $T$, we prove that the number of projective classes of ergodic currents dual to $T$ is bounded above by $3N-5$. We combine Rips induction and splitting induction to define unfolding induction for such an 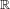$\mathbb{R}$-tree $T$. Given a current ${\it\mu}$ dual to $T$, the unfolding induction produces a sequence of approximations converging towards 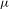${\it\mu}$. We also give a unique ergodicity criterion.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 3 , May 2016 , pp. 745 - 766
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bestvina, M. and Feighn, M.. Stable actions of groups on real trees. Invent. Math. 121(2) (1995), 287–321.Google Scholar
Bestvina, M. and Reynolds, P.. The boundary of the complex of free factors. Preprint, 2012,arXiv:1211.3608.Google Scholar
Bonahon, F.. The geometry of Teichmüller space via geodesic currents. Invent. Math. 92(1) (1988), 139–162.CrossRefGoogle Scholar
Boshernitzan, M. and Kornfeld, I.. Interval translation mappings. Ergod. Th. & Dynam. Sys. 15(5) (1995), 821–832.CrossRefGoogle Scholar
Bowditch, B.. Treelike Structures Arising from Continua and Convergence Groups (Memoirs of the American Mathematical Society, 662). American Mathematical Society, Providence, RI, 1999.CrossRefGoogle Scholar
Bridson, M. R. and Vogtmann, K.. Automorphism groups of free groups, surface groups and free abelian groups. Problems on Mapping Class Groups and Related Topics (Proceedings of Symposia in Pure Mathematics, 74). American Mathematical Society, Providence, RI, 2006, pp. 301–316.Google Scholar
Cohen, M. M. and Lustig, M.. Very small group actions on R -trees and Dehn twist automorphisms. Topology 34(3) (1995), 575–617.Google Scholar
Coulbois, T. and Hilion, A.. Rips induction: index of the dual lamination of an ℝ-tree. Groups Geom. Dyn. 8(1) (2014), 97–134.CrossRefGoogle Scholar
Coulbois, T., Hilion, A. and Lustig, M.. Non-unique ergodicity, observers’ topology and the dual algebraic lamination for ℝ-trees. Illinois J. Math. 51(3) (2007), 897–911.Google Scholar
Coulbois, T., Hilion, A. and Lustig, M.. ℝ-trees and laminations for free groups. I. Algebraic laminations. J. Lond. Math. Soc. (2) 78(3) (2008), 723–736.Google Scholar
Coulbois, T., Hilion, A. and Lustig, M.. ℝ-trees and laminations for free groups. II. The dual lamination of an ℝ-tree. J. Lond. Math. Soc. (2) 78(3) (2008), 737–754.Google Scholar
Coulbois, T., Hilion, A. and Lustig, M.. ℝ-trees and laminations for free groups. III. Currents and dual ℝ-tree metrics. J. Lond. Math. Soc. (2) 78(3) (2008), 755–766.Google Scholar
Coulbois, T., Hilion, A. and Lustig, M.. ℝ-trees, dual laminations, and compact systems of partial isometries. Math. Proc. Cambridge Philos. Soc. 147 (2009), 345–368.Google Scholar
Coulbois, T., Hilion, A. and Reynolds, P.. Indecomposable $F_{N}$-trees and minimal laminations. Groups Geom. Dyn. to appear, Preprint, 2011, arXiv:1110.3506.Google Scholar
Culler, M. and Vogtmann, K.. Moduli of graphs and automorphisms of free groups. Invent. Math. 84 (1986), 91–119.Google Scholar
Durand, F.. Combinatorics on Bratteli diagrams and dynamical systems. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135). Cambridge University Press, Cambridge, 2010, pp. 324–372.Google Scholar
Gaboriau, D.. Générateurs indépendants pour les systèmes d’isométries de dimension un. Ann. Inst. Fourier (Grenoble) 47(1) (1997), 101–122.Google Scholar
Gaboriau, D. and Levitt, G.. The rank of actions on ℝ-trees. Ann. Sci. Éc. Norm. Supér (4) 28(5) (1995), 549–570.Google Scholar
Guirardel, V.. Dynamics of Out(F n) on the boundary of outer space. Ann. Sci. Éc. Norm. Supér (4) 33(4) (2000), 433–465.Google Scholar
Guirardel, V.. Actions of finitely generated groups on ℝ-trees. Ann. Inst. Fourier (Grenoble) 58(1) (2008), 159–211.Google Scholar
Kapovich, I.. The frequency space of a free group. Internat. J. Algebra Comput. 15(5–6) (2005), 939–969.Google Scholar
Kapovich, I.. Currents on free groups. Topological and Asymptotic Aspects of Group Theory (Contemporary Mathematics, 394). American Mathematical Society, Providence, RI, 2006, pp. 149–176.Google Scholar
Kapovich, I. and Lustig, M.. The actions of Out(F k) on the boundary of outer space and on the space of currents: minimal sets and equivariant incompatibility. Ergod. Th. & Dynam. Sys. 27(3) (2007), 827–847.Google Scholar
Kapovich, I. and Lustig, M.. Geometric intersection number and analogues of the curve complex for free groups. Geom. Topol. 13(3) (2009), 1805–1833.Google Scholar
Kapovich, I. and Lustig, M.. Intersection form, laminations and currents on free groups. Geom. Funct. Anal. 19(5) (2010), 1426–1467.Google Scholar
Keane, M.. Non-ergodic interval exchange transformations. Israel J. Math. 26(2) (1977), 188–196.CrossRefGoogle Scholar
Keynes, H. B. and Newton, D.. A ‘minimal’, non-uniquely ergodic interval exchange transformation. Math. Z. 148 (1976), 101–105.Google Scholar
Levitt, G.. Feuilletages des surfaces. Thèse, Université Paris VII, 1983.Google Scholar
Levitt, G. and Lustig, M.. Irreducible automorphisms of F n have north–south dynamics on compactified outer space. J. Inst. Math. Jussieu 2(1) (2003), 59–72.Google Scholar
Levitt, G. and Lustig, M.. Automorphisms of free groups have asymptotically periodic dynamics. J. Reine Angew. Math. 619 (2008), 1–36.Google Scholar
Masur, H.. Interval exchange transformations and measured foliations. Ann. of Math. (2) 115(1) (1982), 169–200.Google Scholar
Papadopoulos, A.. Deux remarques sur la géométrie symplectique de l’espace des feuilletages mesurés sur une surface. Ann. Inst. Fourier (Grenoble) 36(2) (1986), 127–141.CrossRefGoogle Scholar
Paulin, F.. Topologie de Gromov équivariante, structures hyperboliques et arbres réels. Invent. Math. 94(1) (1988), 53–80.Google Scholar
Reynolds, P.. Reducing systems for very small trees. Preprint, 2012, arXiv:1211.3378.Google Scholar
Sataev, E. A.. The number of invariant measures for flows on orientable surfaces. Izv. Akad. Nauk. SSSR Ser. Mat. 39(4) (1975), 860–878.Google Scholar
Yoccoz, J.-C.. Échanges d’intervalles. Cours au Collège de France, 2005.Google Scholar