Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-10T14:30:56.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Ergodic cocycles of IDPFT systems and non-singular Gaussian actions

Part of: Ergodic theory

Published online by Cambridge University Press:  18 February 2021

ALEXANDRE I. DANILENKO Open the ORCID record for ALEXANDRE I. DANILENKO [Opens in a new window]  and
MARIUSZ LEMAŃCZYK
ALEXANDRE I. DANILENKO*
Affiliation:
B. I. Verkin Institute for Low Temperature Physics & Engineering of National Academy of Sciences of Ukraine, 47 Nauky Ave., Kharkiv61103, Ukraine
MARIUSZ LEMAŃCZYK
Affiliation:
Faculty of Mathematics and Computer Science, Nicolaus Copernicus University, ul. Chopina 12/18, 87-100Toruń, Poland (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is proved that each Gaussian cocycle over a mildly mixing Gaussian transformation is either a Gaussian coboundary or sharply weak mixing. The class of non-singular infinite direct products T of transformations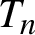 $T_n$ ,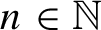 $n\in \mathbb N$ , of finite type is studied. It is shown that if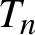 $T_n$ is mildly mixing,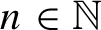 $n\in \mathbb N$ , the sequence of Radon–Nikodym derivatives of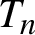 $T_n$ is asymptotically translation quasi-invariant and T is conservative then the Maharam extension of T is sharply weak mixing. This technique provides a new approach to the non-singular Gaussian transformations studied recently by Arano, Isono and Marrakchi.

Keywords

ergodic transformationGaussian cocycleMaharam extension

MSC classification

Primary: 37A40: Nonsingular (and infinite-measure preserving) transformations
Secondary: 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 37A50: Relations with probability theory and stochastic processes
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 5 , May 2022 , pp. 1624 - 1654
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

To the memory of Sergiy Sinel’shchikov, our colleague and friend

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50). American Mathematical Society,Providence, RI, 1997.CrossRefGoogle Scholar
Aaronson, J., Lin, M. and Weiss, B.. Mixing properties of Markov operators and ergodic transformations, and ergodicity of Cartesian products. Israel J. Math. 33 (1979), 198–224.CrossRefGoogle Scholar
Adams, T., Friedman, N. and Silva, C. E.. Rank-one weak mixing for nonsingular transformations. Israel J. Math. 102 (1997), 269–281.CrossRefGoogle Scholar
Arano, Y., Isono, Y. and Marrakchi, A.. Ergodic theory of affine isometric actions on Hilbert spaces. Preprint, 2019, arXiv:1911.04272.Google Scholar
Atkinson, G.. Recurrence of co-cycles and random walks. J. Lond. Math. Soc. 13 (1976), 486–488.CrossRefGoogle Scholar
Avraham-Re’em, N.. On absolutely continuous invariant measures and Krieger-type of Markov subshifts. Preprint, 2020, arXiv:2004.05781.Google Scholar
Bekka, B., de la Harpe, P. and Valette, A.. Kazhdan’s Property (T) (New Mathematical Monographs, 11). Cambridge University Press,Cambridge, 2008.CrossRefGoogle Scholar
Bjørklund, M., Kosloff, Z. and Vaes, S.. Ergodicity and type of nonsingular Bernoulli actions. Invent. Math., to appear.Google Scholar
Danilenko, A. I.. Weak mixing for nonsingular Bernoulli actions of countable amenable groups. Proc. Amer. Math. Soc. 147 (2019), 4439–4450.CrossRefGoogle Scholar
Danilenko, A. I., Kosloff, Z. and Roy, E.. Nonsingular Poisson suspensions. J. Anal. Math., to appear. Preprint, 2020,arXiv:2002.02207.Google Scholar
Danilenko, A. I., Kosloff, Z. and Roy, E.. Generic nonsingular Poisson suspension is of type III 1. Ergod. Th. & Dynam. Sys., to appear. Preprint, 2020,arXiv:2002.05094.CrossRefGoogle Scholar
Danilenko, A. I. and Lemańczyk, M.. K-property for Maharam extensions of non-singular Bernoulli and Markov shifts. Ergod. Theory & Dynam. Sys 39 (2019), 3292–3321.CrossRefGoogle Scholar
Dalecky, Yu. L. and Fomin, S. V.. Measures and Differential Equations in Infinite-Dimensional Space. (Mathematics and Its Applications, 76). Kluwer, Dordrecht, 1991.CrossRefGoogle Scholar
Danilenko, A. I. and Silva, C. E.. Ergodic theory: non-singular transformations. Mathematics of Complexity and Dynamical Systems. Ed. Meyers, R.. Springer,New York, 2012.Google Scholar
Furstenberg, H. and Weiss, B.. The Finite Multipliers of Infinite Ergodic Transformations (Lecture Notes in Mathematics, 688). Springer,Berlin, 1978, pp. 127–132.Google Scholar
Guichardet, A.. Symmetric Hilbert Spaces and Related Topics (Lecture Notes in Mathematics, 261). Springer, Berlin, 1972.CrossRefGoogle Scholar
Hamachi, T. and Osikawa, M.. Ergodic groups of automorphisms and Krieger’s theorems. Sem. Math. Sci. 3 (1981), 1–113.Google Scholar
Kakutani, S.. On equivalence of infinite product measures. Ann. of Math. 49 (1948), 214–224.CrossRefGoogle Scholar
Kosloff, Z.. Proving ergodicity via divergence of ergodic sums. Studia Math. 248 (2019), 191–215.CrossRefGoogle Scholar
Kosloff, Z. and Soo, T.. The orbital equivalence of Bernoulli actions and their Sinai factors. Preprint, 2020,arXiv:2005.02812.CrossRefGoogle Scholar
Lemańczyk, M., Lesigne, E. and Skrenty, D.. Multiplicative Gaussian cocycles. Aequationes Math. 61 (2001), 162–178.Google Scholar
Lemańczyk, M., Parreau, F. and Thouvenot, J.–P.. Gaussian automorphisms whose ergodic self-joinings are Gaussian. Fund. Math. 164 (2000), 253–293.Google Scholar
Maruyama, G.. The harmonic analysis of stationary stochastic processes. Mem. Fac. Sci. Kyushu Univ. Ser. A Math. 4 (1949), 45–106.Google Scholar
Marrakchi, A. and Vaes, S.. Nonsingular Gaussian actions: beyond the mixing case. Preprint, 2020,arXiv:2006.07238.Google Scholar
Nikulin, M. S.. Hellinger distance. Encyclopedia of Mathematics. Ed. Hazewinkel, M.. Kluwer, Dordrecht, 1995.Google Scholar
Roy, E.. Poisson suspensions and infinite ergodic theory. Ergod. Th. & Dynam. Sys. 29 (2009), 667–683.CrossRefGoogle Scholar
Schmidt, K.. Cocycles of Ergodic Transformation Groups (Macmillan Lectures in Mathematics, 1). Macmillan,Delhi, 1977.Google Scholar
Schmidt, K. and Walters, P.. Mildly mixing actions of locally compact groups. Proc. London Math. Soc. 45 (1982), 506–518.CrossRefGoogle Scholar
Silva, C. E. and Thieullen, P.. A skew product entropy for nonsingular transformations. J. Lond. Math. Soc. 52 (1995), 497–516.CrossRefGoogle Scholar
Skorohod, A. V.. Integration in Hilbert Spaces. Springer,Berlin, 1974.CrossRefGoogle Scholar