Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Mosher, Lee
1990.
Correction to ‘Equivariant spectral decomposition for flows with a ℤ-action’.
Ergodic Theory and Dynamical Systems,
Vol. 10,
Issue. 4,
p.
787.
Mosher, Lee
1991.
Surfaces and branched surfaces transverse to pseudo-Anosov flows on 3-manifolds.
Journal of Differential Geometry,
Vol. 34,
Issue. 1,
Mosher, Lee
1992.
Dynamical systems and the homology norm of a 3-manifold II.
Inventiones Mathematicae,
Vol. 107,
Issue. 1,
p.
243.
Morales, C.
2010.
The deficiency of a cohomology class.
Proceedings of the American Mathematical Society,
Vol. 138,
Issue. 12,
p.
4321.
Landry, Michael P.
2022.
Veering triangulations and the Thurston norm: Homology to isotopy.
Advances in Mathematics,
Vol. 396,
Issue. ,
p.
108102.


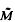 equipped with a free, properly discontinuous, cocompact ℤ-action, and a flow
equipped with a free, properly discontinuous, cocompact ℤ-action, and a flow 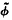 on
on 