Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T03:53:17.478Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivalence classes of codimension-one cut-and-project nets

Published online by Cambridge University Press:  11 November 2014

ALAN HAYNES
ALAN HAYNES*
Affiliation:
Department of Mathematics, University of York, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that in any totally irrational cut-and-project setup with codimension (internal space dimension) one, it is possible to choose sections (windows) in non-trivial ways so that the resulting sets are bounded displacement equivalent to lattices. Our proof demonstrates that for any irrational ${\it\alpha}$, regardless of Diophantine type, there is a collection of intervals in 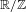$\mathbb{R}/\mathbb{Z}$ which is closed under translation, contains intervals of arbitrarily small length, and along which the discrepancy of the sequence 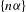$\{n{\it\alpha}\}$ is bounded above uniformly by a constant.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 3 , May 2016 , pp. 816 - 831
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliste-Prieto, J., Coronel, D. and Gambaudo, J.-M.. Linearly repetitive Delone sets are rectifiable. Ann. Inst. H. Poincaré Anal. Non Linéaire 30(2) (2013), 275–290.Google Scholar
Baake, M. and Moody, R.. Weighted Dirac combs with pure point diffraction. J. Reine Angew. Math. 573 (2004), 61–94.Google Scholar
Beresnevich, V., Haynes, A., Vaaler, J. and Velani, S.. On the sum of the reciprocals of the sequence $n{\it\alpha}~\text{mod}~1$. Preprint.Google Scholar
Burago, D. and Kleiner, B.. Separated nets in Euclidean space and Jacobians of bi-Lipschitz maps. Geom. Funct. Anal. 8 (1998), 273–282.Google Scholar
Burago, D. and Kleiner, B.. Rectifying separated nets. Geom. Funct. Anal. 12(1) (2002), 80–92.Google Scholar
Haynes, A., Kelly, M. and Weiss, B.. Equivalence relations on separated nets arising from linear toral flows. Proc. Lond. Math. Soc. to appear.Google Scholar
Hecke, E.. Über analytische Funktionen und die Verteilung von Zahlen mod eins. Abh. Math. Semin. Univ. Hambg. 1(1) (1922), 54–76 (in German).Google Scholar
Laczkovich, M.. Uniformly spread discrete sets in ℝd. J. Lond. Math. Soc. (2) 46 (1992), 39–57.Google Scholar
Kesten, H.. On a conjecture of Erdős and Szüsz related to uniform distribution mod 1. Acta Arith. 12 (1966–1967), 193–212.Google Scholar
McMullen, C.. Lipschitz maps and nets in Euclidean space. Geom. Funct. Anal. 8 (1998), 304–314.Google Scholar
Meyer, Y.. Quasicrystals, Diophantine approximation and algebraic numbers. Beyond Quasicrystals (Les Houches, 1994). Springer, Berlin, 1995, pp. 3–16.Google Scholar
Moody, R.. Recent developments in the mathematics of diffraction. Z. Kristallogr. 223 (2008), 795–800.CrossRefGoogle Scholar
Ostrowski, A.. Mathematische Miszellen IX, Notiz zur theorie der Diophantischen approximationen. Jahresber. Dtsch. Math.-Ver. 36 (1927), 178–180 (in German).Google Scholar
Ostrowski, A.. Mathematische Miszellen XVI, Notiz zur theorie der Diophantischen approximationen. Jahresber. Dtsch. Math.-Ver. 39 (1930), 34–46 (in German).Google Scholar
Rockett, A. and Szüsz, P.. Continued Fractions. World Scientific, Singapore, 1992.Google Scholar
Schmidt, W. M.. Irregularities of distribution VII. Acta Arith. 21 (1972), 45–50.Google Scholar
Solomon, Y.. Tilings and separated nets with similarities to the integer lattice. Israel J. Math. 181 (2011), 445–460.Google Scholar