Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-18T02:00:05.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Equilibrium measures of the natural extension of 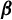$\boldsymbol{\beta}$-shifts

Part of: Limit theorems Topological dynamics Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  04 May 2021

C.-E. PFISTER  and
W. G. SULLIVAN
C.-E. PFISTER*
Affiliation:
Section of Mathematics, Faculty of Basic Sciences, EPFL, CH-1015Lausanne, Switzerland
W. G. SULLIVAN
Affiliation:
School of Mathematics and Statistics, UCD, Belfield, Dublin 4, Ireland (e-mail: [email protected])
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a necessary and sufficient condition on 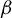$\beta $ of the natural extension of a 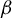$\beta $ -shift, so that any equilibrium measure for a function of bounded total oscillations is a weak Gibbs measure.

Keywords

beta-shiftssymbolic dynamicsequilibrium measuresweak Gibbs measures

MSC classification

Primary: 37B10: Symbolic dynamics 37D35: Thermodynamic formalism, variational principles, equilibrium states
Secondary: 60F10: Large deviations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 7 , July 2022 , pp. 2415 - 2430
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470), 2nd revised edn. Ed. Chazottes, J.-R.. Springer, Berlin, 2008.CrossRefGoogle Scholar
Capocaccia, D.. A definition of Gibbs state for a compact set with a ${\mathbb{Z}}^{\nu }$ action. Comm. Math. Phys. 48 (1976), 85–88.CrossRefGoogle Scholar
Climenhaga, V., Thompson, D. J. and Yamamoto, K.. Large deviations for systems with non-uniform structure. Trans. Amer. Math. Soc. 369 (2017), 4167–4192.CrossRefGoogle Scholar
Haydn, N. T. A. and Ruelle, D.. Equivalence of Gibbs and equilibrium states for homeomorphisms satisfying expansiveness and specification. Comm. Math. Phys. 148 (1992), 155–167.CrossRefGoogle Scholar
Parry, W.. On the $\beta$ -expansions of real numbers. Acta Math. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Pfister, C.-E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Application to the $\beta$ -shifts. Nonlinearity 18 (2005), 237–261.CrossRefGoogle Scholar
Pfister, C.-E. and Sullivan, W. G.. Weak Gibbs measures and large deviations. Nonlinearity 31 (2018), 49–53.CrossRefGoogle Scholar
Pfister, C.-E. and Sullivan, W. G.. Asymptotic decoupling and weak Gibbs measures for finite alphabet shift spaces. Nonlinearity 33 (2020), 4799–4817.CrossRefGoogle Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Rockafellar, R. T.. Convex Analysis (Princeton Mathematical Series, 28). Princeton University Press, Princeton, NJ, 1970.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic Formalism (Encyclopedia of Mathematics and its Applications, 5). Addison-Wesley, Reading, MA, 1978.Google Scholar
Schmeling, J.. Symbolic dynamics for $\beta$ -shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17 (1997), 675–694.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1982.CrossRefGoogle Scholar