Article contents
Equidistribution of joinings under off-diagonal polynomial flows of nilpotent Lie groups
Published online by Cambridge University Press: 05 September 2012
Abstract
Let 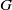 $G$ be a connected nilpotent Lie group. Given probability-preserving
$G$ be a connected nilpotent Lie group. Given probability-preserving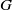 $G$-actions
$G$-actions 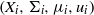 $(X_i,\Sigma _i,\mu _i,u_i)$,
$(X_i,\Sigma _i,\mu _i,u_i)$, 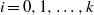 $i=0,1,\ldots ,k$, and also polynomial maps
$i=0,1,\ldots ,k$, and also polynomial maps 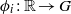 $\phi _i:\mathbb {R}\to G$,
$\phi _i:\mathbb {R}\to G$, 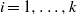 $i=1,\ldots ,k$, we consider the trajectory of a joining
$i=1,\ldots ,k$, we consider the trajectory of a joining 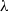 $\lambda $ of the systems
$\lambda $ of the systems 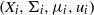 $(X_i,\Sigma _i,\mu _i,u_i)$ under the ‘off-diagonal’ flow
$(X_i,\Sigma _i,\mu _i,u_i)$ under the ‘off-diagonal’ flow 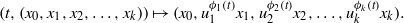 \[ (t,(x_0,x_1,x_2,\ldots ,x_k))\mapsto (x_0,u_1^{\phi _1(t)}x_1,u_2^{\phi _2(t)}x_2,\ldots ,u_k^{\phi _k(t)}x_k). \]
\[ (t,(x_0,x_1,x_2,\ldots ,x_k))\mapsto (x_0,u_1^{\phi _1(t)}x_1,u_2^{\phi _2(t)}x_2,\ldots ,u_k^{\phi _k(t)}x_k). \]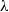 $\lambda $ is equidistributed under this flow with respect to some limit joining
$\lambda $ is equidistributed under this flow with respect to some limit joining 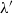 $\lambda '$. This is deduced from the stronger fact of norm convergence for a system of multiple ergodic averages, related to those arising in Furstenberg’s approach to the study of multiple recurrence. It is also shown that the limit joining
$\lambda '$. This is deduced from the stronger fact of norm convergence for a system of multiple ergodic averages, related to those arising in Furstenberg’s approach to the study of multiple recurrence. It is also shown that the limit joining 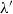 $\lambda '$ is invariant under the subgroup of
$\lambda '$ is invariant under the subgroup of 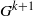 $G^{k+1}$generated by the image of the off-diagonal flow, in addition to the diagonal subgroup.
$G^{k+1}$generated by the image of the off-diagonal flow, in addition to the diagonal subgroup.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 2
- Cited by


