1 Introduction
Horocyclic flows associated to a geodesic flow have been extensively studied on compact surfaces with constant negative curvature [Reference Furstenberg10], and later on compact surfaces with variable negative curvature [Reference Marcus15, Reference Marcus16]. They are uniquely ergodic and mixing, and they have zero topological entropy, among other properties. More generally, on negatively curved compact manifolds of any dimension, the Bowen–Margulis measure is the unique measure invariant under the unstable foliation, and all the horospheres are equidistributed towards this measure [Reference Roblin20]. In this paper, we have two goals: first, we produce a result on the equidistribution of horospheres for rank 1 manifolds with non-positive curvature; and second, for the case of surfaces, we prove the unique ergodicity of the horocyclic flow restricted to a well-chosen subset of rank 1 vectors.
Babillot gave a simple proof of the mixing property of the geodesic flow and showed the equidistribution of horospheres under the action of this flow towards certain product measures for manifolds with negative curvature [Reference Babillot1]. For the Bowen–Margulis measure, the equidistribution of horospheres can be stated as follows.
Theorem. [Reference Babillot1, Theorem 3]
Let M be a non-elementary complete connected Riemannian manifold with negative curvature bounded away from
![]() $0$
. Assume that the geodesic flow
$0$
. Assume that the geodesic flow
![]() $g_t$
on the unitary tangent bundle
$g_t$
on the unitary tangent bundle
![]() $T^1M$
of M is topologically mixing on the set of non-wandering vectors, and that the Bowen–Margulis measure
$T^1M$
of M is topologically mixing on the set of non-wandering vectors, and that the Bowen–Margulis measure
![]() $\mu $
is finite. Then, for every unstable horosphere
$\mu $
is finite. Then, for every unstable horosphere
![]() $H\subset T^1M$
, every open subset U of H containing a non-wandering vector is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
$H\subset T^1M$
, every open subset U of H containing a non-wandering vector is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
![]() $T^1M$
, we have
$T^1M$
, we have
where
![]() $\{\mu _H\}_H$
are the conditional measures of the Bowen–Margulis measure
$\{\mu _H\}_H$
are the conditional measures of the Bowen–Margulis measure
![]() $\mu $
along the unstable foliation.
$\mu $
along the unstable foliation.
We refer the reader to [Reference Paulin, Pollicott and Schapira18] for the so-called Patterson–Sullivan construction of the Bowen–Margulis measure in negative curvature. Several criteria for the finiteness of this measure are given in [Reference Pit and Schapira19].
The Bowen–Margulis measure can be generalized to non-positively curved rank 1 manifolds. G. Knieper constructed this measure in [Reference Knieper12], following the method pioneered by Patterson and Sullivan [Reference Patterson17, Reference Sullivan21], and proved that it is the unique measure of maximal entropy when the manifold is compact. In this paper we explain an optimal way to generalize the equidistribution of horospheres towards Bowen–Margulis for non-positively curved rank 1 manifolds, following the approach of Babillot.
In the equidistribution theorem, we consider the averages of a function with respect to a measure
![]() $\mu _H$
, which we will define in §2.2, associated to the horocycle H. On a negatively curved manifold, if U is an open subset of H containing a non-wandering vector, the
$\mu _H$
, which we will define in §2.2, associated to the horocycle H. On a negatively curved manifold, if U is an open subset of H containing a non-wandering vector, the
![]() $\mu _H$
-measure of U is positive, so it makes perfect sense to average a function over U. However, on manifolds of non-positive curvature, not every open subset of a horocycle containing a non-wandering vector has positive measure. As an example, we take a non-flat surface containing a flat cylinder (Figure 1). All the vertical vectors with base point in a longitudinal segment of the cylinder are in the same unstable horocycle. The set U formed by these vectors has zero
$\mu _H$
-measure of U is positive, so it makes perfect sense to average a function over U. However, on manifolds of non-positive curvature, not every open subset of a horocycle containing a non-wandering vector has positive measure. As an example, we take a non-flat surface containing a flat cylinder (Figure 1). All the vertical vectors with base point in a longitudinal segment of the cylinder are in the same unstable horocycle. The set U formed by these vectors has zero
![]() $\mu _H$
-measure, which is clear from its construction, although each vector of U is periodic and, in particular, non-wandering.
$\mu _H$
-measure, which is clear from its construction, although each vector of U is periodic and, in particular, non-wandering.
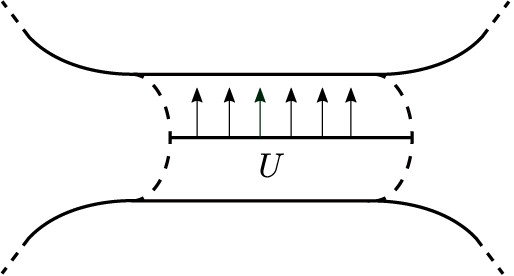
Figure 1 A surface with a flat cylinder.
Theorem A shows that, under a certain hypothesis, an open subset U of a horosphere H is equidistributed in time, as soon as U has positive
![]() $\mu _H$
-measure. We emphasize that rank 1 compact manifolds with non-positive curvature satisfy the hypothesis, so there is equidistribution.
$\mu _H$
-measure. We emphasize that rank 1 compact manifolds with non-positive curvature satisfy the hypothesis, so there is equidistribution.
Theorem A. Let M be a non-positively curved non-elementary complete connected Riemannian manifold with a closed rank 1 geodesic. Assume that the geodesic flow
![]() $g_t$
on the unitary tangent bundle
$g_t$
on the unitary tangent bundle
![]() $T^1M$
of M is topologically mixing on the set of non-wandering vectors, and that the Bowen–Margulis measure
$T^1M$
of M is topologically mixing on the set of non-wandering vectors, and that the Bowen–Margulis measure
![]() $\mu $
is finite. Then, for every horosphere
$\mu $
is finite. Then, for every horosphere
![]() $H\subset T^1 M$
containing a non-wandering vector, every open subset U of H of finite but positive
$H\subset T^1 M$
containing a non-wandering vector, every open subset U of H of finite but positive
![]() $\mu _H$
-measure is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
$\mu _H$
-measure is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
![]() $T^1M$
, we have
$T^1M$
, we have
In the case of a piece of horocycle U with zero
![]() $\mu _H$
-measure, it might be reasonable to wonder if there is equidistribution with respect to another measure giving a positive value to U, for instance, the Lesbesgue measure, which is very natural. The example of the surface with a flat cylinder shows that this is also not possible, because the geodesic flow acts periodically on the piece of horocycle U; then, for a well-chosen function f, the averages of
$\mu _H$
-measure, it might be reasonable to wonder if there is equidistribution with respect to another measure giving a positive value to U, for instance, the Lesbesgue measure, which is very natural. The example of the surface with a flat cylinder shows that this is also not possible, because the geodesic flow acts periodically on the piece of horocycle U; then, for a well-chosen function f, the averages of
![]() $f\circ g_t$
on U could oscillate endlessly.
$f\circ g_t$
on U could oscillate endlessly.
In the second part of this paper we study the case of surfaces, which is easier to deal with as the horospheres can be parametrized by a flow. The dynamical properties of horocyclic flows are well understood in some situations. For instance, on a negatively curved compact surface, the Bowen–Margulis measure is the unique probability measure invariant under the horocyclic flow [Reference Marcus15]. For geometrically finite manifolds, there is a classification of the Radon measures invariant under the horocyclic flow [Reference Roblin20, Corollary 6.5].
We follow Marcus’s method, based on the definition of a parametrization of the horocyclic flow by the measures on the horocycles. Unfortunately, it is not possible to define an analogous parametrization on the whole space for rank 1 surfaces with non-positive curvature, due to the presence of flat regions. We avoid this difficulty, by restricting our system to the set
![]() $\Sigma $
of vectors whose horocycle contains a rank 1 vector recurrent under the geodesic flow. Under the hypothesis of the theorem, this set has full Bowen–Margulis measure and is
$\Sigma $
of vectors whose horocycle contains a rank 1 vector recurrent under the geodesic flow. Under the hypothesis of the theorem, this set has full Bowen–Margulis measure and is
![]() $G_\delta $
-dense in the unitary tangent bundle. Thanks to the equidistribution of the horocycles of Theorem A and a part of the strategy followed by Coudène in [Reference Coudène4], we prove the unique ergodicity of the horocyclic flow on
$G_\delta $
-dense in the unitary tangent bundle. Thanks to the equidistribution of the horocycles of Theorem A and a part of the strategy followed by Coudène in [Reference Coudène4], we prove the unique ergodicity of the horocyclic flow on
![]() $\Sigma $
for manifolds that satisfy the duality condition, which means that the non-wandering set of the geodesic flow is the whole unitary tangent bundle. Rank 1 compact surfaces with non-positive curvature are included.
$\Sigma $
for manifolds that satisfy the duality condition, which means that the non-wandering set of the geodesic flow is the whole unitary tangent bundle. Rank 1 compact surfaces with non-positive curvature are included.
Theorem B. Let M be an orientable rank 1 complete connected Riemannian surface with non-positive curvature satisfying the duality condition. Assume that the Bowen–Margulis measure
![]() $\mu $
is finite. Then every finite Borel measure on
$\mu $
is finite. Then every finite Borel measure on
![]() $\Sigma $
invariant under the horocyclic flow
$\Sigma $
invariant under the horocyclic flow
![]() $h_s$
is a constant multiple of the Bowen–Margulis measure
$h_s$
is a constant multiple of the Bowen–Margulis measure
![]() $\mu |_\Sigma $
restricted to
$\mu |_\Sigma $
restricted to
![]() $\Sigma $
.
$\Sigma $
.
In this paper we only work with expanding horospheres and expanding horocyclic flows, but all the results have an analogy in the contracting setting.
2 Measures on the horocycles and equidistribution
2.1 Notation
Let M be a complete connected Riemannian manifold of non-positive curvature and denote by
![]() $g_t:T^1M\rightarrow T^1M$
the geodesic flow on the unitary tangent bundle
$g_t:T^1M\rightarrow T^1M$
the geodesic flow on the unitary tangent bundle
![]() $T^1M$
of M. Recall that the rank of a vector v in
$T^1M$
of M. Recall that the rank of a vector v in
![]() $T^1 M$
, denoted by
$T^1 M$
, denoted by
![]() $\operatorname {\mathrm {rank}} v$
, is the dimension of the parallel Jacobi fields along the geodesic tangent to v. There is always a parallel Jacobi field in the tangent direction of the geodesic, so the rank must be between
$\operatorname {\mathrm {rank}} v$
, is the dimension of the parallel Jacobi fields along the geodesic tangent to v. There is always a parallel Jacobi field in the tangent direction of the geodesic, so the rank must be between
![]() $1$
and the dimension of M. We say that the manifold M is of rank 1 if it contains at least one vector of rank 1. Let us start with some standard definitions and recall the most important facts about rank 1 manifolds.
$1$
and the dimension of M. We say that the manifold M is of rank 1 if it contains at least one vector of rank 1. Let us start with some standard definitions and recall the most important facts about rank 1 manifolds.
Most of the reasoning unfolds on the universal cover
![]() $\tilde {M}$
of M. We consider the Riemannian distance d on
$\tilde {M}$
of M. We consider the Riemannian distance d on
![]() $\tilde {M}$
and the distance
$\tilde {M}$
and the distance
![]() $d_1$
associated to the Sasaki metric on
$d_1$
associated to the Sasaki metric on
![]() $T^1\tilde {M}$
. A geodesic ray is, by definition, a map
$T^1\tilde {M}$
. A geodesic ray is, by definition, a map
![]() $\sigma : [0,+\infty )\rightarrow \tilde {M}$
that minimizes length. Two geodesic rays
$\sigma : [0,+\infty )\rightarrow \tilde {M}$
that minimizes length. Two geodesic rays
![]() $\sigma _1,\sigma _2$
are asymptotic if the distance
$\sigma _1,\sigma _2$
are asymptotic if the distance
![]() $d(\sigma _1(t),\sigma _2(t))$
is uniformly bounded for all
$d(\sigma _1(t),\sigma _2(t))$
is uniformly bounded for all
![]() $t\ge 0$
. The boundary at infinity
$t\ge 0$
. The boundary at infinity
![]() $\partial \tilde {M}$
is the set of asymptotic classes of rays. We refer the reader to [Reference Ballmann2, Reference Ballmann, Gromov and Schroeder3] for a better understanding of this construction.
$\partial \tilde {M}$
is the set of asymptotic classes of rays. We refer the reader to [Reference Ballmann2, Reference Ballmann, Gromov and Schroeder3] for a better understanding of this construction.
The Busemann cocycle at
![]() $\xi $
in
$\xi $
in
![]() $\partial \tilde {M}$
between x and y in
$\partial \tilde {M}$
between x and y in
![]() $\tilde {M}$
is defined as
$\tilde {M}$
is defined as
where
![]() $\sigma $
is any ray in the class
$\sigma $
is any ray in the class
![]() $\xi $
. If v is a vector in
$\xi $
. If v is a vector in
![]() $T^1\tilde {M}$
, the points at infinity
$T^1\tilde {M}$
, the points at infinity
![]() $v_-$
and
$v_-$
and
![]() $v_+$
in
$v_+$
in
![]() $\partial \tilde {M}$
are respectively the asymptotic classes of the negative and positive rays tangent to v. We can define the (unstable) horosphere of v as the set
$\partial \tilde {M}$
are respectively the asymptotic classes of the negative and positive rays tangent to v. We can define the (unstable) horosphere of v as the set
where
![]() $\pi :T^1\tilde {M}\rightarrow \tilde {M}$
is the projection to the base. The point
$\pi :T^1\tilde {M}\rightarrow \tilde {M}$
is the projection to the base. The point
![]() $v_-$
in
$v_-$
in
![]() $ \partial \tilde {M}$
is called the center of the horosphere
$ \partial \tilde {M}$
is called the center of the horosphere
![]() $H^u(v)$
. Horospheres are
$H^u(v)$
. Horospheres are
![]() $C^1 $
submanifolds of
$C^1 $
submanifolds of
![]() $T^1\tilde {M}$
of dimension
$T^1\tilde {M}$
of dimension
![]() ${\dim M~-1}$
.
${\dim M~-1}$
.
We also use the notation
![]() $\partial ^2\tilde {M}=(\partial \tilde {M}\times \partial \tilde {M})\setminus \Delta $
, where
$\partial ^2\tilde {M}=(\partial \tilde {M}\times \partial \tilde {M})\setminus \Delta $
, where
![]() $\Delta $
is the diagonal of
$\Delta $
is the diagonal of
![]() $\partial \tilde {M}\times \partial \tilde {M}$
, and define the map
$\partial \tilde {M}\times \partial \tilde {M}$
, and define the map
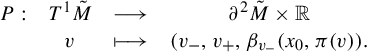 $$ \begin{align*} \begin{matrix} P: & T^1 \tilde{M} & \longrightarrow & \partial^2 \tilde{M} \times \mathbb{R} \\ & v & \longmapsto & (v_-,v_+,\beta_{v_-}(x_0,\pi(v)). \end{matrix} \end{align*} $$
$$ \begin{align*} \begin{matrix} P: & T^1 \tilde{M} & \longrightarrow & \partial^2 \tilde{M} \times \mathbb{R} \\ & v & \longmapsto & (v_-,v_+,\beta_{v_-}(x_0,\pi(v)). \end{matrix} \end{align*} $$
It is known that this map is a homeomorphism when the curvature is negatively pinched, but both the injectivity and the surjectivity may fail in the context of non-positively curved rank 1 manifolds. Nevertheless, restricted to rank 1 vectors, P is still a homeomorphism onto its image [Reference Ballmann2].
In the sequel, we identify M with the quotient of
![]() $\tilde {M}$
by some discrete subgroup of isometries
$\tilde {M}$
by some discrete subgroup of isometries
![]() $\Gamma $
, which is isomorphic to the fundamental group of M. The limit set
$\Gamma $
, which is isomorphic to the fundamental group of M. The limit set
![]() $\Lambda (\Gamma )$
is the set of accumulation points of an orbit
$\Lambda (\Gamma )$
is the set of accumulation points of an orbit
![]() $\Gamma x_0$
,
$\Gamma x_0$
,
![]() $x_0\in \tilde {M}$
, in
$x_0\in \tilde {M}$
, in
![]() $\tilde {M}\cup \partial \tilde {M}$
. It does not depend on the choice of
$\tilde {M}\cup \partial \tilde {M}$
. It does not depend on the choice of
![]() $x_0$
and it is contained in the boundary at infinity
$x_0$
and it is contained in the boundary at infinity
![]() $\partial \tilde {M}$
. We also define the non-wandering set
$\partial \tilde {M}$
. We also define the non-wandering set
![]() $\Omega $
to be the set
$\Omega $
to be the set
![]() $\{ v\in T^1 \tilde {M} \,|\, v_-,v_+\in \Lambda (\Gamma ) \}$
. The name of this set comes from the fact that its projection to
$\{ v\in T^1 \tilde {M} \,|\, v_-,v_+\in \Lambda (\Gamma ) \}$
. The name of this set comes from the fact that its projection to
![]() $T^1M$
is the topological non-wandering set of the geodesic flow. In order to have some complexity in the geodesic flow, we require that
$T^1M$
is the topological non-wandering set of the geodesic flow. In order to have some complexity in the geodesic flow, we require that
![]() $\Gamma $
(or M) is non-elementary, which means that the limit set
$\Gamma $
(or M) is non-elementary, which means that the limit set
![]() $\Lambda (\Gamma )$
is infinite.
$\Lambda (\Gamma )$
is infinite.
A
![]() $\delta $
-dimensional conformal density,
$\delta $
-dimensional conformal density,
![]() $\delta \ge 0$
, is a family of finite Borel measures
$\delta \ge 0$
, is a family of finite Borel measures
![]() $\{\mu _x\}_{x\in \tilde {M}}$
on
$\{\mu _x\}_{x\in \tilde {M}}$
on
![]() $\partial \tilde {M}$
supported by the limit set
$\partial \tilde {M}$
supported by the limit set
![]() $\Lambda (\Gamma )$
and such that any two measures
$\Lambda (\Gamma )$
and such that any two measures
![]() $\mu _x,\mu _y$
, where
$\mu _x,\mu _y$
, where
![]() $x,y\in \tilde {M}$
, are equivalent and satisfy the relation
$x,y\in \tilde {M}$
, are equivalent and satisfy the relation
![]() $({\mathrm {d} \mu _y}/{\mathrm {d} \mu _x})(\xi )=\exp {(-\delta \beta _\xi (y,x))}$
. In addition, we say that such a family of measures is
$({\mathrm {d} \mu _y}/{\mathrm {d} \mu _x})(\xi )=\exp {(-\delta \beta _\xi (y,x))}$
. In addition, we say that such a family of measures is
![]() $\Gamma $
-invariant if
$\Gamma $
-invariant if
![]() $\gamma _*\mu _x=\mu _{\gamma x}$
for all
$\gamma _*\mu _x=\mu _{\gamma x}$
for all
![]() $\gamma \in \Gamma ,\,x\in \tilde {M}$
. The Patterson construction provides examples of invariant
$\gamma \in \Gamma ,\,x\in \tilde {M}$
. The Patterson construction provides examples of invariant
![]() $\delta (\Gamma )$
-dimensional conformal densities, where
$\delta (\Gamma )$
-dimensional conformal densities, where
![]() $\delta (\Gamma )$
is the critical exponent of
$\delta (\Gamma )$
is the critical exponent of
![]() $\Gamma $
(see [Reference Knieper11], for example). Henceforth, we will fix a point
$\Gamma $
(see [Reference Knieper11], for example). Henceforth, we will fix a point
![]() $x_0\in \tilde {M}$
and denote by
$x_0\in \tilde {M}$
and denote by
![]() $\mu _{x_0}$
an element of an invariant
$\mu _{x_0}$
an element of an invariant
![]() $\delta $
-dimensional conformal density.
$\delta $
-dimensional conformal density.
2.2 Definition of the Bowen–Margulis measure
We now define a product measure on the unitary tangent bundle of
![]() $\tilde {M}$
, which will pass to the quotient
$\tilde {M}$
, which will pass to the quotient
![]() $T^1M$
, as Knieper did in [Reference Knieper12] for a compact manifold. Consider the set of geodesic endpoints
$T^1M$
, as Knieper did in [Reference Knieper12] for a compact manifold. Consider the set of geodesic endpoints
![]() $E(\tilde {M}):=\{(v_-,v_+)\in \partial ^2\tilde {M}\,|\,v\in T^1\tilde {M} \}$
. For every
$E(\tilde {M}):=\{(v_-,v_+)\in \partial ^2\tilde {M}\,|\,v\in T^1\tilde {M} \}$
. For every
![]() $(\xi ,\eta )\in E (\tilde {M})$
, the set
$(\xi ,\eta )\in E (\tilde {M})$
, the set
![]() $\pi (P^{-1}(\{(\xi ,\eta )\}\times \mathbb {R}))$
is non-empty, and it has been shown to be a flat totally geodesic submanifold of
$\pi (P^{-1}(\{(\xi ,\eta )\}\times \mathbb {R}))$
is non-empty, and it has been shown to be a flat totally geodesic submanifold of
![]() $\tilde {M}$
[Reference Eberlein9]. In fact, it is either a single geodesic or a flat totally geodesic submanifold of dimension at least
$\tilde {M}$
[Reference Eberlein9]. In fact, it is either a single geodesic or a flat totally geodesic submanifold of dimension at least
![]() $2$
. No matter what form the submanifold
$2$
. No matter what form the submanifold
![]() $\pi (P^{-1}(\{(\xi ,\eta )\}\times \mathbb {R}))$
takes, we denote by
$\pi (P^{-1}(\{(\xi ,\eta )\}\times \mathbb {R}))$
takes, we denote by
![]() $\operatorname {\mathrm {Vol}}$
its induced volume measure.
$\operatorname {\mathrm {Vol}}$
its induced volume measure.
Firstly, we define a measure
![]() $\bar {\mu }$
on
$\bar {\mu }$
on
![]() $E(\tilde {M})$
, which we extend to
$E(\tilde {M})$
, which we extend to
![]() $\partial ^2\tilde {M}$
, by its density
$\partial ^2\tilde {M}$
, by its density
where
![]() $p_{\xi ,\eta }$
is any point in
$p_{\xi ,\eta }$
is any point in
![]() $\pi (P^{-1}(\{(\xi ,\eta )\}\times \mathbb {R}))$
. The definition does not depend on the choices of
$\pi (P^{-1}(\{(\xi ,\eta )\}\times \mathbb {R}))$
. The definition does not depend on the choices of
![]() $p_{\xi ,\eta }$
, and
$p_{\xi ,\eta }$
, and
![]() $\bar {\mu }$
is invariant under the diagonal action of
$\bar {\mu }$
is invariant under the diagonal action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $\partial ^2\tilde {M}$
. Now, the measure
$\partial ^2\tilde {M}$
. Now, the measure
![]() $\mu $
on
$\mu $
on
![]() $T^1 \tilde {M}$
associated to
$T^1 \tilde {M}$
associated to
![]() $\mu _{x_0}$
gives the value
$\mu _{x_0}$
gives the value
to a Borel subset
![]() $A\subset T^1\tilde {M}$
. It is clear that this measure is both
$A\subset T^1\tilde {M}$
. It is clear that this measure is both
![]() $\Gamma $
- and
$\Gamma $
- and
![]() $g_t$
-invariant. The
$g_t$
-invariant. The
![]() $g_t$
-invariant measure obtained on the quotient
$g_t$
-invariant measure obtained on the quotient
![]() $T^1 M$
will also be denoted by
$T^1 M$
will also be denoted by
![]() $\mu $
, for simplicity of notation.
$\mu $
, for simplicity of notation.
In the sequel, we assume that M contains a closed rank 1 geodesic. Many authors have studied the ergodic properties of this measure in this setting. Link and Picaud gave a version of the Hopf–Tsuji–Sullivan dichotomy (see [Reference Babillot1
Reference Ballmann, Gromov and Schroeder3, Reference Babillot1
Reference Coudène4]). In this paper we will always be in the conservative case of the dichotomy:
![]() $\Gamma $
is of divergence type, the radial limit set has full
$\Gamma $
is of divergence type, the radial limit set has full
![]() $\mu _{x_0}$
-measure and the system
$\mu _{x_0}$
-measure and the system
![]() $(T^1M,g_t,\mu )$
is conservative and ergodic. Furthermore, in this case there is a unique conformal density
$(T^1M,g_t,\mu )$
is conservative and ergodic. Furthermore, in this case there is a unique conformal density
![]() $\mu _{x_0}$
and its dimension is the critical exponent
$\mu _{x_0}$
and its dimension is the critical exponent
![]() $\delta =\delta (\Gamma )$
of
$\delta =\delta (\Gamma )$
of
![]() $\Gamma $
, this measure
$\Gamma $
, this measure
![]() $\mu _{x_0}$
has no point masses, and the measure class of
$\mu _{x_0}$
has no point masses, and the measure class of
![]() $\mu _{x_0}$
is ergodic under the action of
$\mu _{x_0}$
is ergodic under the action of
![]() $\Gamma $
. We refer to
$\Gamma $
. We refer to
![]() $\mu $
as the Bowen–Margulis measure. Whenever M is compact, it turns out that the Bowen–Margulis measure
$\mu $
as the Bowen–Margulis measure. Whenever M is compact, it turns out that the Bowen–Margulis measure
![]() $\mu $
is the unique measure of maximal entropy up to a multiplicative constant as proved by Knieper in [Reference Knieper12].
$\mu $
is the unique measure of maximal entropy up to a multiplicative constant as proved by Knieper in [Reference Knieper12].
Let
![]() $\mathcal {H}$
be the set of unstable horospheres in
$\mathcal {H}$
be the set of unstable horospheres in
![]() $T^1 \tilde {M}$
and let
$T^1 \tilde {M}$
and let
![]() $\Gamma $
act on
$\Gamma $
act on
![]() $\mathcal {H}$
. There is a simple identification of
$\mathcal {H}$
. There is a simple identification of
![]() $\mathcal {H}$
by its point at infinity and the value of the Busemann cocycle: the map
$\mathcal {H}$
by its point at infinity and the value of the Busemann cocycle: the map
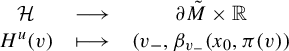 $$ \begin{align*} \begin{matrix} \mathcal{H} & \longrightarrow & \partial \tilde{M} \times \mathbb{R} \\ H^u(v) & \longmapsto & (v_-,\beta_{v_-}(x_0,\pi(v)) \end{matrix} \end{align*} $$
$$ \begin{align*} \begin{matrix} \mathcal{H} & \longrightarrow & \partial \tilde{M} \times \mathbb{R} \\ H^u(v) & \longmapsto & (v_-,\beta_{v_-}(x_0,\pi(v)) \end{matrix} \end{align*} $$
is bijective. This allows us to define a
![]() $\Gamma $
-invariant measure
$\Gamma $
-invariant measure
![]() $\hat {\mu }$
on the space of horospheres
$\hat {\mu }$
on the space of horospheres
![]() $ \mathcal {H}$
by the density
$ \mathcal {H}$
by the density
where
![]() $H^u(\xi ,t)$
is the unstable horosphere with coordinates
$H^u(\xi ,t)$
is the unstable horosphere with coordinates
![]() $(\xi ,t)\in \partial \tilde {M}\times \mathbb {R}$
.
$(\xi ,t)\in \partial \tilde {M}\times \mathbb {R}$
.
We can now define a family
![]() $\{\mu _{H}\}_{H\in \mathcal {H}}$
of measures on each horosphere that has good properties, analogous to the negative curvature case. For each horosphere H, we consider the projection to the positive endpoint
$\{\mu _{H}\}_{H\in \mathcal {H}}$
of measures on each horosphere that has good properties, analogous to the negative curvature case. For each horosphere H, we consider the projection to the positive endpoint
![]() $P_H:H\rightarrow \partial \tilde {M}\setminus \{\xi \}$
, where
$P_H:H\rightarrow \partial \tilde {M}\setminus \{\xi \}$
, where
![]() $\xi $
is the center of H. Let us treat a point as a
$\xi $
is the center of H. Let us treat a point as a
![]() $0$
-manifold, for the sake of simplicity. For any vector v in
$0$
-manifold, for the sake of simplicity. For any vector v in
![]() $T^1\tilde {M}$
, the set of base points of vectors on the horosphere
$T^1\tilde {M}$
, the set of base points of vectors on the horosphere
![]() $H^u(v)$
that are also positively asymptotic to v (that is, the set
$H^u(v)$
that are also positively asymptotic to v (that is, the set
![]() $\pi (P_{H^u(v)}^{-1}(v_+))$
), is a totally geodesic submanifold of
$\pi (P_{H^u(v)}^{-1}(v_+))$
), is a totally geodesic submanifold of
![]() $\pi (P^{-1}((v_-,v_+)\times \mathbb {R}))$
. We denote its volume measure by
$\pi (P^{-1}((v_-,v_+)\times \mathbb {R}))$
. We denote its volume measure by
![]() $\operatorname {\mathrm {Vol}}$
, with the convention that it is the delta measure when the submanifold consists of a single point. For each
$\operatorname {\mathrm {Vol}}$
, with the convention that it is the delta measure when the submanifold consists of a single point. For each
![]() $\eta \in \partial \tilde {M}\setminus \{v_-\}$
, we choose
$\eta \in \partial \tilde {M}\setminus \{v_-\}$
, we choose
![]() $w\in P_{H^u(v)}^{-1} (\eta ))$
and write
$w\in P_{H^u(v)}^{-1} (\eta ))$
and write
![]() $\phi _v(\eta )=e^{\delta \beta _{\eta }(x_0,\pi (w))}$
, which in fact only depends on
$\phi _v(\eta )=e^{\delta \beta _{\eta }(x_0,\pi (w))}$
, which in fact only depends on
![]() $\eta $
, but not on w. The measure
$\eta $
, but not on w. The measure
![]() $\mu _{H^u(v)}$
assigns the value
$\mu _{H^u(v)}$
assigns the value
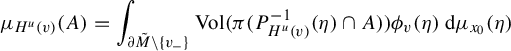 $$ \begin{align*} \mu_{H^u(v)}(A)=\int_{\partial\tilde{M}\setminus\{v_-\}} \operatorname{\mathrm{Vol}}(\pi (P_{H^u(v)}^{-1}(\eta)\cap A)) \phi_v(\eta) \,\mathrm{d} \mu_{x_0}(\eta) \end{align*} $$
$$ \begin{align*} \mu_{H^u(v)}(A)=\int_{\partial\tilde{M}\setminus\{v_-\}} \operatorname{\mathrm{Vol}}(\pi (P_{H^u(v)}^{-1}(\eta)\cap A)) \phi_v(\eta) \,\mathrm{d} \mu_{x_0}(\eta) \end{align*} $$
to a subset
![]() $A\subset H^u(v)$
.
$A\subset H^u(v)$
.
We list the main properties of these measures that follow from the definition.
-
(i) If
 $w\in H^u(v)$
, then
$w\in H^u(v)$
, then
 $\mu _{H^u(v)}=\mu _{H^u(w)}$
. Hence, we can speak of a family
$\mu _{H^u(v)}=\mu _{H^u(w)}$
. Hence, we can speak of a family
 $\{\mu _{H}\}_{H\in \mathcal {H}}$
of measures on each horosphere.
$\{\mu _{H}\}_{H\in \mathcal {H}}$
of measures on each horosphere. -
(ii) They are
 $\Gamma $
-invariant; that is, for all
$\Gamma $
-invariant; that is, for all
 $\gamma $
in
$\gamma $
in
 $\Gamma $
and all H in
$\Gamma $
and all H in
 $\mathcal {H}$
, we have
$\mathcal {H}$
, we have
 $\gamma _*\mu _H=\mu _{\gamma H}$
.
$\gamma _*\mu _H=\mu _{\gamma H}$
. -
(iii) They are exponentially expanded by the geodesic flow:
 $\mu _{g_tH}=e^{\delta t}(g_t)_*\mu _{H}$
.
$\mu _{g_tH}=e^{\delta t}(g_t)_*\mu _{H}$
. -
(iv) The measure
 $\mu $
is the product of
$\mu $
is the product of
 $\{\mu _{H}\}_{H\in \mathcal {H}}$
by
$\{\mu _{H}\}_{H\in \mathcal {H}}$
by
 $\hat {\mu }$
: for all
$\hat {\mu }$
: for all
 $A\subset T^1 \tilde {M}$
,(2)
$A\subset T^1 \tilde {M}$
,(2) $$ \begin{align} \mu(A)=\int_{\mathcal{H}} \mu_H(A\cap H)\, \mathrm{d} \hat{\mu}(H). \end{align} $$
$$ \begin{align} \mu(A)=\int_{\mathcal{H}} \mu_H(A\cap H)\, \mathrm{d} \hat{\mu}(H). \end{align} $$
For our purposes, we assume that the Bowen–Margulis measure
![]() $\mu $
on the space
$\mu $
on the space
![]() $T^1M$
is finite, hence the geodesic flow is conservative, according to the Poincaré recurrence theorem, and there is only one conformal density
$T^1M$
is finite, hence the geodesic flow is conservative, according to the Poincaré recurrence theorem, and there is only one conformal density
![]() $\mu _{x_0}$
. Our goal is to find an equidistribution result in the sense that the
$\mu _{x_0}$
. Our goal is to find an equidistribution result in the sense that the
![]() $\mu _H$
-averages of functions on a horosphere H tend to the
$\mu _H$
-averages of functions on a horosphere H tend to the
![]() $\mu $
-averages on the whole space. The starting point is always the mixing property of the geodesic flow with respect to the Bowen–Margulis measure
$\mu $
-averages on the whole space. The starting point is always the mixing property of the geodesic flow with respect to the Bowen–Margulis measure
![]() $\mu $
. The next result says that this property is equivalent to the topological mixing of the geodesic flow on
$\mu $
. The next result says that this property is equivalent to the topological mixing of the geodesic flow on
![]() $\Omega $
. We do not know if this equivalence has been stated in this generality, although it can be expected and the main part of the work is already published.
$\Omega $
. We do not know if this equivalence has been stated in this generality, although it can be expected and the main part of the work is already published.
There is a third equivalent property related to the length of the closed geodesics, analogous to what happens in negative curvature. We define the rank 1 length spectrum as the set of lengths of rank 1 closed geodesics. We say that the rank 1 length spectrum is non-arithmetic if the rank 1 length spectrum generates a dense subgroup of
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Theorem 2.1. Let M be a rank 1 non-positively curved non-elementary complete connected Riemannian manifold. Assume that the Bowen–Margulis measure
![]() $\mu $
is finite. Then the following assertions are equivalent.
$\mu $
is finite. Then the following assertions are equivalent.
-
(i) The geodesic flow
 $g_t$
is topologically mixing on the non-wandering set
$g_t$
is topologically mixing on the non-wandering set
 $\Omega $
.
$\Omega $
. -
(ii) The geodesic flow
 $g_t$
is mixing with respect to the Bowen–Margulis measure
$g_t$
is mixing with respect to the Bowen–Margulis measure
 $\mu $
.
$\mu $
. -
(iii) The rank 1 length spectrum is non-arithmetic.
Proof. (ii)
![]() $\implies $
(i) The mixing property with respect to a measure implies the topological mixing on the support of the measure. In our case, the support of
$\implies $
(i) The mixing property with respect to a measure implies the topological mixing on the support of the measure. In our case, the support of
![]() $\mu $
is the non-wandering set
$\mu $
is the non-wandering set
![]() $\Omega $
, so the implication is proved.
$\Omega $
, so the implication is proved.
(i)
![]() $\implies $
(iii) We reproduce the reasoning used in negative curvature [Reference Dal’bo5]. Since the set of rank 1 vectors is open [Reference Ballmann2], we can find a closed ball B of certain radius only containing rank 1 vectors. Let
$\implies $
(iii) We reproduce the reasoning used in negative curvature [Reference Dal’bo5]. Since the set of rank 1 vectors is open [Reference Ballmann2], we can find a closed ball B of certain radius only containing rank 1 vectors. Let
![]() $\varepsilon>0$
be a given number. We apply the closing lemma for the rank 1 set [Reference Eberlein9, Proposition 4.5.15]: there exist constants
$\varepsilon>0$
be a given number. We apply the closing lemma for the rank 1 set [Reference Eberlein9, Proposition 4.5.15]: there exist constants
![]() $T_0>0$
and
$T_0>0$
and
![]() $\delta>0$
such that, for every
$\delta>0$
such that, for every
![]() $v\in B$
and
$v\in B$
and
![]() $t\ge T_0$
with
$t\ge T_0$
with
![]() $d_1(v,g_t(v))\le \delta $
, there exists a periodic rank 1 vector
$d_1(v,g_t(v))\le \delta $
, there exists a periodic rank 1 vector
![]() $v'$
at distance
$v'$
at distance
![]() $d_1(v,v')\le \varepsilon $
, where the period
$d_1(v,v')\le \varepsilon $
, where the period
![]() $t'$
of v satisfies
$t'$
of v satisfies
![]() $|t-t'|<\varepsilon $
.
$|t-t'|<\varepsilon $
.
There exists a non-empty open subset U of
![]() $\Omega $
of diameter smaller than
$\Omega $
of diameter smaller than
![]() $\delta $
and such that
$\delta $
and such that
![]() $U\subset B$
. Since the geodesic flow on
$U\subset B$
. Since the geodesic flow on
![]() $\Omega $
is topologically mixing, there exists a number
$\Omega $
is topologically mixing, there exists a number
![]() $T\ge T_0$
such that, for all
$T\ge T_0$
such that, for all
![]() $t\ge T$
, we have
$t\ge T$
, we have
![]() $U\cap g_t(U)\not = \emptyset $
. In particular, there is a rank 1 vector v in B satisfying
$U\cap g_t(U)\not = \emptyset $
. In particular, there is a rank 1 vector v in B satisfying
![]() $d_1(v,g_t(v))\le \delta $
. Hence, for each
$d_1(v,g_t(v))\le \delta $
. Hence, for each
![]() $t \ge T$
, there exists a periodic rank 1 vector of period in
$t \ge T$
, there exists a periodic rank 1 vector of period in
![]() $[t-\varepsilon ,t+\varepsilon ]$
. Since
$[t-\varepsilon ,t+\varepsilon ]$
. Since
![]() $\varepsilon $
is arbitrary, this proves that the rank 1 length spectrum is non-arithmetic.
$\varepsilon $
is arbitrary, this proves that the rank 1 length spectrum is non-arithmetic.
(iii)
![]() $\implies $
(ii) This implication may be the hardest, but it is essentially done in the proof of [Reference Babillot1], asserting that the geodesic flow is mixing with respect to
$\implies $
(ii) This implication may be the hardest, but it is essentially done in the proof of [Reference Babillot1], asserting that the geodesic flow is mixing with respect to
![]() $\mu $
on a compact manifold. All the arguments work for a rank 1 manifold with finite Bowen–Margulis measure, but at the end, instead of applying the compactness, we can use the assumption of non-arithmeticity of the length spectrum.
$\mu $
on a compact manifold. All the arguments work for a rank 1 manifold with finite Bowen–Margulis measure, but at the end, instead of applying the compactness, we can use the assumption of non-arithmeticity of the length spectrum.
To summarize, in all statements M is a non-elementary non-positively curved complete connected manifold with a closed geodesic of rank 1 such that the geodesic flow is topologically mixing on
![]() $\Omega $
and such that the Bowen–Margulis measure
$\Omega $
and such that the Bowen–Margulis measure
![]() $\mu $
is finite.
$\mu $
is finite.
2.3 Equidistribution of horocycles
We start with a local result showing that near rank 1 vectors there is equidistribution: for a function
![]() $f:T^1M\rightarrow \mathbb {R}$
, the average on a horosphere of its lift
$f:T^1M\rightarrow \mathbb {R}$
, the average on a horosphere of its lift
![]() $\tilde {f}:T^1\tilde {M}\rightarrow \mathbb {R}$
pushed by the geodesic flow converges to the average of f with respect to the Bowen–Margulis measure.
$\tilde {f}:T^1\tilde {M}\rightarrow \mathbb {R}$
pushed by the geodesic flow converges to the average of f with respect to the Bowen–Margulis measure.
Proposition 2.2. Let M be a non-positively curved non-elementary complete connected Riemannian manifold with a closed rank 1 geodesic. Assume that the geodesic flow
![]() $g_t$
on
$g_t$
on
![]() $T^1M$
is topologically mixing on
$T^1M$
is topologically mixing on
![]() $\Omega $
and that the Bowen–Margulis measure
$\Omega $
and that the Bowen–Margulis measure
![]() $\mu $
is finite. Then, for every rank 1 vector
$\mu $
is finite. Then, for every rank 1 vector
![]() $v\in \Omega \subset T^1 \tilde {M}$
, there exists an open subset U of
$v\in \Omega \subset T^1 \tilde {M}$
, there exists an open subset U of
![]() $H^u(v)$
containing v which is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
$H^u(v)$
containing v which is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
![]() $T^1 M$
and every Borel neighborhood
$T^1 M$
and every Borel neighborhood
![]() $V\subset U$
of v, we have
$V\subset U$
of v, we have
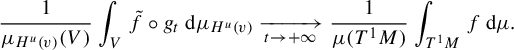 $$ \begin{align*} \frac{1}{\mu_{H^u(v)}(V)}\int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H^u(v)} \xrightarrow[t \to +\infty]{} \frac{1}{\mu(T^1 M)} \int_{T^1 M}f \,\mathrm{d} \mu. \end{align*} $$
$$ \begin{align*} \frac{1}{\mu_{H^u(v)}(V)}\int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H^u(v)} \xrightarrow[t \to +\infty]{} \frac{1}{\mu(T^1 M)} \int_{T^1 M}f \,\mathrm{d} \mu. \end{align*} $$
Proof. We follow the same strategy as Babillot in [Reference Babillot1], which involves approximating the integral on a piece of horosphere by the integral of the same function on a box around that piece, and then use the mixing property of the geodesic flow with respect to
![]() $\mu $
. The added difficulty is to find a box with a good system of coordinates, which is done by avoiding the vectors of higher rank.
$\mu $
. The added difficulty is to find a box with a good system of coordinates, which is done by avoiding the vectors of higher rank.
Let v be a rank 1 vector in
![]() $\Omega $
and denote its horosphere by H. From [Reference Ballmann2, Lemma III.3.1] we know that there exist disjoint connected neighborhoods
$\Omega $
and denote its horosphere by H. From [Reference Ballmann2, Lemma III.3.1] we know that there exist disjoint connected neighborhoods
![]() $A_1$
and
$A_1$
and
![]() $A_2$
of
$A_2$
of
![]() $v_-$
and
$v_-$
and
![]() $v_+$
, respectively, in
$v_+$
, respectively, in
![]() $\partial \tilde {M}$
such that: for every
$\partial \tilde {M}$
such that: for every
![]() $(\xi ,\eta )\in A_1\times A_2$
there exists a unique geodesic from
$(\xi ,\eta )\in A_1\times A_2$
there exists a unique geodesic from
![]() $\xi $
to
$\xi $
to
![]() $\eta $
, and it has rank 1. This allows us to consider a coordinate neighborhood of v via the map P of the form
$\eta $
, and it has rank 1. This allows us to consider a coordinate neighborhood of v via the map P of the form
![]() $A_1\times A_2 \times \mathbb {R}$
.
$A_1\times A_2 \times \mathbb {R}$
.
We claim that the proposition is true with
![]() $U=P_H^{-1}( A_2)$
. Consider any neighborhood
$U=P_H^{-1}( A_2)$
. Consider any neighborhood
![]() $V\subset U$
of v and write
$V\subset U$
of v and write
![]() $V_+:=\{w_+\,|\,w\in V\}$
for its projection to the boundary at infinity
$V_+:=\{w_+\,|\,w\in V\}$
for its projection to the boundary at infinity
![]() $\partial \tilde {M}$
. Since v is non-wandering, its endpoints are in the limit set, and this guarantees that
$\partial \tilde {M}$
. Since v is non-wandering, its endpoints are in the limit set, and this guarantees that
![]() $V_+$
and V have positive measure. We notice that the integral on V of a function h of
$V_+$
and V have positive measure. We notice that the integral on V of a function h of
![]() $T^1 \tilde {M}$
can be written in coordinates as
$T^1 \tilde {M}$
can be written in coordinates as
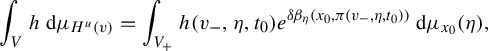 $$ \begin{align*} \int_V h\,\mathrm{d}\mu_{H^u(v)}=\int_{V_+}h(v_-,\eta , t_0)e^{\delta \beta_\eta (x_0,\pi (v_-,\eta, t_0))} \, \mathrm{d}\mu_{x_0}(\eta), \end{align*} $$
$$ \begin{align*} \int_V h\,\mathrm{d}\mu_{H^u(v)}=\int_{V_+}h(v_-,\eta , t_0)e^{\delta \beta_\eta (x_0,\pi (v_-,\eta, t_0))} \, \mathrm{d}\mu_{x_0}(\eta), \end{align*} $$
where
![]() $t_0$
has the value
$t_0$
has the value
![]() $\beta _{v_-}(x_0,\pi (v))$
, because the volume
$\beta _{v_-}(x_0,\pi (v))$
, because the volume
![]() $\operatorname {\mathrm {Vol}}$
is always
$\operatorname {\mathrm {Vol}}$
is always
![]() $1$
on rank 1 vectors. This is because
$1$
on rank 1 vectors. This is because
![]() $P^{-1} (\{(v_-,\eta ,t_0)\}$
consists of just one vector when v is of rank 1. Otherwise, the flat strip theorem [Reference Ballmann2, Corollary I.5.8(ii)] asserts that v bounds a flat totally geodesic surface, which is not possible for a rank 1 vector.
$P^{-1} (\{(v_-,\eta ,t_0)\}$
consists of just one vector when v is of rank 1. Otherwise, the flat strip theorem [Reference Ballmann2, Corollary I.5.8(ii)] asserts that v bounds a flat totally geodesic surface, which is not possible for a rank 1 vector.
Given
![]() $\varepsilon>0$
, we can find a small connected neighborhood
$\varepsilon>0$
, we can find a small connected neighborhood
![]() $B\subset A_1$
of
$B\subset A_1$
of
![]() $v_-$
and a number
$v_-$
and a number
![]() $r>0$
such that:
$r>0$
such that:
-
(i) for all
 $\xi \in B$
, for all
$\xi \in B$
, for all
 $\eta \in V_+$
,
$\eta \in V_+$
,
 $ 1-\varepsilon \le e^{\delta \beta _\eta (\pi (v_-,\eta , t_0),\,\pi (\xi ,\eta , t_0))} \le 1+\varepsilon $
;
$ 1-\varepsilon \le e^{\delta \beta _\eta (\pi (v_-,\eta , t_0),\,\pi (\xi ,\eta , t_0))} \le 1+\varepsilon $
; -
(ii) for all
 $(\xi ,\eta ) \in B\times V_+$
, for all
$(\xi ,\eta ) \in B\times V_+$
, for all
 $s\in [-r,r]$
, for all
$s\in [-r,r]$
, for all
 $t\ge 0$
,
$t\ge 0$
,
 $ | \tilde {f}(v_-,\eta , t_0+t)-\tilde {f}(\xi , \eta , t_0+t+s)|<\varepsilon $
.
$ | \tilde {f}(v_-,\eta , t_0+t)-\tilde {f}(\xi , \eta , t_0+t+s)|<\varepsilon $
.
Property (i) follows from the continuity of the map P on the coordinate neighborhood, and the continuity of the projection
![]() $\pi $
and of the Busemann function. We use the fact that
$\pi $
and of the Busemann function. We use the fact that
![]() $V_+$
is relatively compact to assert that the inequality holds uniformly in
$V_+$
is relatively compact to assert that the inequality holds uniformly in
![]() $\eta \in V_+$
. For property (ii), we apply the uniform continuity of
$\eta \in V_+$
. For property (ii), we apply the uniform continuity of
![]() $\tilde {f}$
, and then we choose B and r so that the points
$\tilde {f}$
, and then we choose B and r so that the points
![]() $(v_-,\eta , t_0)$
and
$(v_-,\eta , t_0)$
and
![]() $(\xi ,\eta , t_0+s)$
are close enough for
$(\xi ,\eta , t_0+s)$
are close enough for
![]() $\xi \in B$
and
$\xi \in B$
and
![]() $s\in [-r,r]$
, uniformly in
$s\in [-r,r]$
, uniformly in
![]() $\eta \in V_+$
. Since these points are in the same weak stable leaf, the distance between them does not increase when they are pushed by the geodesic flow, which allows us to deduce the above property for all
$\eta \in V_+$
. Since these points are in the same weak stable leaf, the distance between them does not increase when they are pushed by the geodesic flow, which allows us to deduce the above property for all
![]() $t\ge 0$
. Again the condition
$t\ge 0$
. Again the condition
![]() $v\in \Omega $
implies that
$v\in \Omega $
implies that
![]() $v_-\in \Lambda (\Gamma )$
, which ensures that B has positive measure.
$v_-\in \Lambda (\Gamma )$
, which ensures that B has positive measure.
These estimates allow one to compare the average of
![]() $\tilde {f}\circ g_t$
on the set V with respect to
$\tilde {f}\circ g_t$
on the set V with respect to
![]() $\mu _{H^u(v)}$
and the average of the same function on the box of the form
$\mu _{H^u(v)}$
and the average of the same function on the box of the form
![]() $P^{-1}(B\times V_+\times [t_0,t_0+r])$
with respect to the measure
$P^{-1}(B\times V_+\times [t_0,t_0+r])$
with respect to the measure
![]() $\mu $
by means of the product structure of
$\mu $
by means of the product structure of
![]() $\mu $
(equation (1)). More precisely, for all non-negative t,
$\mu $
(equation (1)). More precisely, for all non-negative t,
 $$ \begin{align*} \bigg[\frac{ \int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H^u(v)} }{ \mu_{H^u(v)}(V) }-\varepsilon \bigg] \frac{1-\varepsilon}{1+\varepsilon} &\le \frac{ \int_{P ^{-1}(B\times V_+\times [t_0,t_0+r])} \tilde{f}\circ g_t \, \mathrm{d} \mu }{\mu(P^{-1}(B\times V_+\times [t_0,t_0+r]))}\\ &\le \bigg[\frac{ \int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H^u(v)} }{ \mu_{H^u(v)}(V) }+\varepsilon \bigg] \frac{1+\varepsilon}{1-\varepsilon}. \end{align*} $$
$$ \begin{align*} \bigg[\frac{ \int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H^u(v)} }{ \mu_{H^u(v)}(V) }-\varepsilon \bigg] \frac{1-\varepsilon}{1+\varepsilon} &\le \frac{ \int_{P ^{-1}(B\times V_+\times [t_0,t_0+r])} \tilde{f}\circ g_t \, \mathrm{d} \mu }{\mu(P^{-1}(B\times V_+\times [t_0,t_0+r]))}\\ &\le \bigg[\frac{ \int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H^u(v)} }{ \mu_{H^u(v)}(V) }+\varepsilon \bigg] \frac{1+\varepsilon}{1-\varepsilon}. \end{align*} $$
Moreover, we may assume that the neighborhood
![]() $P^{-1}(B\times A_2\times [t_0,t_0+r])\subset T^1\tilde {M}$
is homeomorphic to its projection on the unit tangent bundle of the manifold M. Then, since the geodesic flow is mixing with respect to
$P^{-1}(B\times A_2\times [t_0,t_0+r])\subset T^1\tilde {M}$
is homeomorphic to its projection on the unit tangent bundle of the manifold M. Then, since the geodesic flow is mixing with respect to
![]() $\mu $
, the average of
$\mu $
, the average of
![]() $\tilde {f}\circ g_t$
in
$\tilde {f}\circ g_t$
in
![]() $P^{-1}(B\times V_+\times [t_0,t_0+r])$
converges to
$P^{-1}(B\times V_+\times [t_0,t_0+r])$
converges to
![]() $({1}/{\mu {(T^1 M)}})\int f\, \mathrm {d} \mu $
when t goes to infinity. We have thus shown the equidistribution of U.
$({1}/{\mu {(T^1 M)}})\int f\, \mathrm {d} \mu $
when t goes to infinity. We have thus shown the equidistribution of U.
To deduce a global result, we need to understand what happens on vectors of rank different from
![]() $1$
, and the next two lemmas will be crucial. The unstable manifold of v in
$1$
, and the next two lemmas will be crucial. The unstable manifold of v in
![]() $T^1\tilde {M}$
is the set
$T^1\tilde {M}$
is the set
![]() $W^u(v)$
is a subset of the unstable horosphere
$W^u(v)$
is a subset of the unstable horosphere
![]() $H^u (v)$
, but they are not necessarily equal in non-positive curvature.
$H^u (v)$
, but they are not necessarily equal in non-positive curvature.
Lemma 2.3. Let M be a rank 1 non-positively curved non-elementary complete connected Riemannian manifold. If v is a rank 1 recurrent vector in
![]() $T^1\tilde {M}$
, then its unstable horosphere coincides with its unstable manifold,
$T^1\tilde {M}$
, then its unstable horosphere coincides with its unstable manifold,
![]() $H^u(v)=W^u(v)$
, and it consists of rank 1 vectors exclusively.
$H^u(v)=W^u(v)$
, and it consists of rank 1 vectors exclusively.
Proof. The fact that the unstable manifold and the horosphere coincide is already proved in [Reference Knieper12, Proposition 4.1]. Let w be in
![]() $W^u(v)$
and r be its rank; we will see that r is
$W^u(v)$
and r be its rank; we will see that r is
![]() $1$
. Since v is negatively recurrent there exist a sequence
$1$
. Since v is negatively recurrent there exist a sequence
![]() $t_n\rightarrow -\infty $
and isometries
$t_n\rightarrow -\infty $
and isometries
![]() $\gamma _n\in \Gamma $
such that
$\gamma _n\in \Gamma $
such that
![]() $\gamma _n(g_{t_n}(v))\rightarrow v$
when
$\gamma _n(g_{t_n}(v))\rightarrow v$
when
![]() $n\to \infty $
. Now we have
$n\to \infty $
. Now we have
and the rank of
![]() $\gamma _n g_{t_n}(w)$
is the same as the rank of w, r. Since v is a limit of vectors of rank r and the rank function is upper semi-continuous, we deduce
$\gamma _n g_{t_n}(w)$
is the same as the rank of w, r. Since v is a limit of vectors of rank r and the rank function is upper semi-continuous, we deduce
![]() $r\le \operatorname {\mathrm {rank}} v = 1$
.
$r\le \operatorname {\mathrm {rank}} v = 1$
.
Lemma 2.4. Let M be a non-positively curved non-elementary complete connected Riemannian manifold with a closed rank 1 geodesic. Assume that the Bowen–Margulis measure
![]() $\mu $
is finite and that the geodesic flow
$\mu $
is finite and that the geodesic flow
![]() $g_t$
on
$g_t$
on
![]() $T^1M$
is ergodic with respect to the
$T^1M$
is ergodic with respect to the
![]() $\mu $
. Then, for every horocycle H, the set of vectors in H of rank equal to or greater than
$\mu $
. Then, for every horocycle H, the set of vectors in H of rank equal to or greater than
![]() $2$
is
$2$
is
![]() $\mu _H$
-negligible.
$\mu _H$
-negligible.
Proof. Let
![]() $Rec^1\subset T^1\tilde {M}$
be the set of rank 1 vectors which are recurrent under
$Rec^1\subset T^1\tilde {M}$
be the set of rank 1 vectors which are recurrent under
![]() $g_t$
on the quotient
$g_t$
on the quotient
![]() $T^1 M$
and let
$T^1 M$
and let
![]() $S\subset T^1\tilde {M}$
be the set of vectors of rank 2 or higher. We claim that the projections to the boundary of these two sets are disjoint,
$S\subset T^1\tilde {M}$
be the set of vectors of rank 2 or higher. We claim that the projections to the boundary of these two sets are disjoint,
![]() $Rec^1_+\cap S_+=\emptyset $
. Otherwise, there are vectors
$Rec^1_+\cap S_+=\emptyset $
. Otherwise, there are vectors
![]() $v\in Rec^1$
and
$v\in Rec^1$
and
![]() $w\in S$
such that
$w\in S$
such that
![]() $v_+=w_+$
. By Lemma 2.3, the unstable horosphere of
$v_+=w_+$
. By Lemma 2.3, the unstable horosphere of
![]() $-v$
only contains vectors of rank 1. The geodesic associated to
$-v$
only contains vectors of rank 1. The geodesic associated to
![]() $-w$
intersects this horosphere
$-w$
intersects this horosphere
![]() $H^u(-v)$
(Figure 2), so w should have rank 1, which is a contradiction.
$H^u(-v)$
(Figure 2), so w should have rank 1, which is a contradiction.
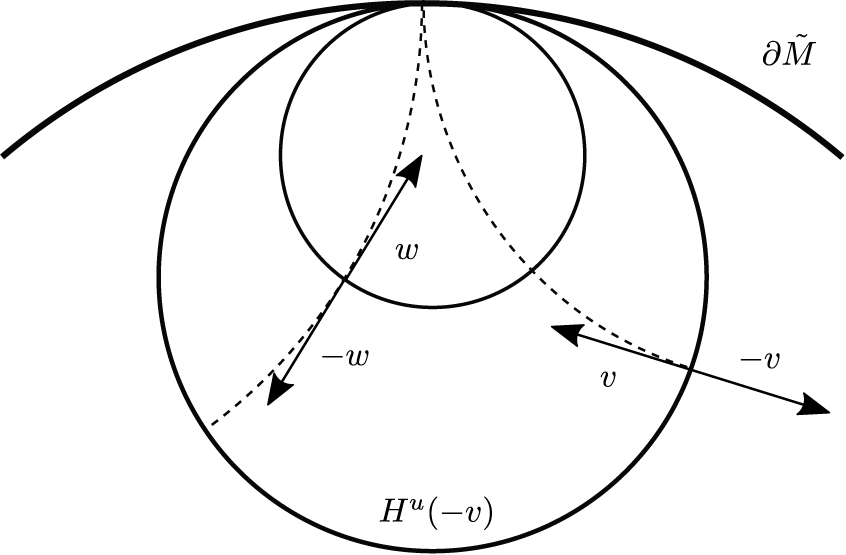
Figure 2 Vectors v and w in the proof of Lemma 2.4.
Around a non-wandering rank 1 vector there is a neighborhood only consisting of rank 1 vectors, and this neighborhood has positive measure because it intersects the support of
![]() $\mu $
. By hypothesis, the manifold M contains a closed rank 1 geodesic, which is an example of a non-wandering rank 1 geodesic. The set of rank 1 vectors has positive measure, and it is invariant under the geodesic flow. So the set of rank 1 vectors has full measure because of the ergodicity of
$\mu $
. By hypothesis, the manifold M contains a closed rank 1 geodesic, which is an example of a non-wandering rank 1 geodesic. The set of rank 1 vectors has positive measure, and it is invariant under the geodesic flow. So the set of rank 1 vectors has full measure because of the ergodicity of
![]() $\mu $
. In consequence, the set of rank 1 recurrent vectors
$\mu $
. In consequence, the set of rank 1 recurrent vectors
![]() $Rec^1$
also has full
$Rec^1$
also has full
![]() $\mu $
-measure in view of the Poincaré recurrence theorem. By the product structure of
$\mu $
-measure in view of the Poincaré recurrence theorem. By the product structure of
![]() $\mu $
, we see that
$\mu $
, we see that
![]() $Rec^1_+$
has positive
$Rec^1_+$
has positive
![]() $\mu _{x_0}$
-measure. Finally,
$\mu _{x_0}$
-measure. Finally,
![]() $Rec^1_+$
is a
$Rec^1_+$
is a
![]() $\Gamma $
-invariant set, so we deduce that
$\Gamma $
-invariant set, so we deduce that
![]() $Rec^1_+$
has full
$Rec^1_+$
has full
![]() $\mu _{x_0}$
-measure because
$\mu _{x_0}$
-measure because
![]() $\Gamma $
acts ergodically.
$\Gamma $
acts ergodically.
Therefore,
![]() $S_+$
is negligible. The endpoints of higher rank vectors in
$S_+$
is negligible. The endpoints of higher rank vectors in
![]() $H^u(v)$
are clearly in
$H^u(v)$
are clearly in
![]() $S_+$
and, using the definition of the measure on the horosphere, we obtain
$S_+$
and, using the definition of the measure on the horosphere, we obtain
![]() $\mu _{H^u(v)}(S\cap H^u(v))=0$
.
$\mu _{H^u(v)}(S\cap H^u(v))=0$
.
We can finally prove Theorem A, which we have reformulated in terms of horospheres on the universal cover
![]() $\tilde {M}$
. On the horospheres centered at the limit set, every open set with positive and finite measure is equidistributed (Figure 3). Being positive is equivalent to having a non-wandering rank 1 vector. In particular, all relatively compact neighborhoods of non-wandering rank 1 vectors are equidistributed.
$\tilde {M}$
. On the horospheres centered at the limit set, every open set with positive and finite measure is equidistributed (Figure 3). Being positive is equivalent to having a non-wandering rank 1 vector. In particular, all relatively compact neighborhoods of non-wandering rank 1 vectors are equidistributed.
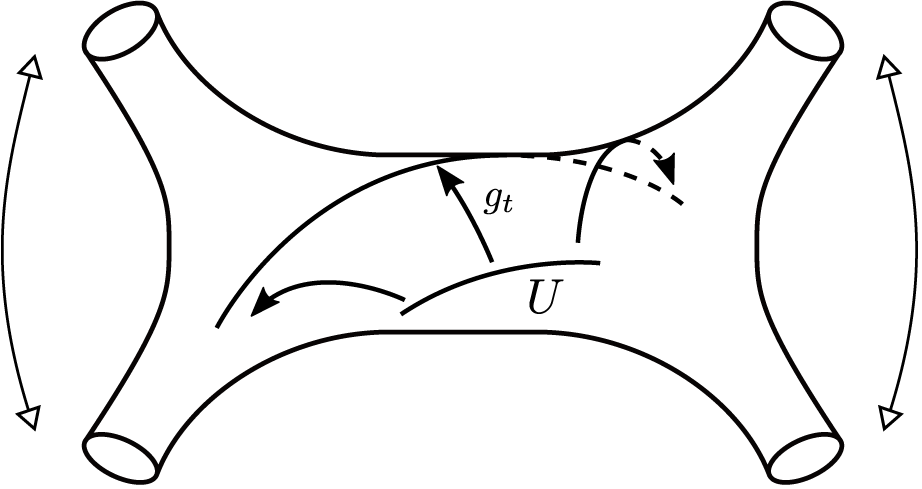
Figure 3 The average of f on the image of an open subset U of a horosphere H by the geodesic flow
![]() $g_t$
with respect to
$g_t$
with respect to
![]() $\mu _H$
tends to the average of f with respect to
$\mu _H$
tends to the average of f with respect to
![]() $\mu $
.
$\mu $
.
Theorem 2.5. Let M be a non-positively curved non-elementary complete connected Riemannian manifold with a closed rank 1 geodesic. Assume that the geodesic flow
![]() $g_t$
on
$g_t$
on
![]() $T^1M$
is topologically mixing on
$T^1M$
is topologically mixing on
![]() $ \Omega $
and that the Bowen–Margulis measure
$ \Omega $
and that the Bowen–Margulis measure
![]() $\mu $
is finite. Then, for every horosphere
$\mu $
is finite. Then, for every horosphere
![]() $H\subset T^1 \tilde {M}$
centered at
$H\subset T^1 \tilde {M}$
centered at
![]() $\Lambda (\Gamma )$
, every open subset U of H of finite but positive
$\Lambda (\Gamma )$
, every open subset U of H of finite but positive
![]() $\mu _H$
-measure is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
$\mu _H$
-measure is equidistributed under the action of the geodesic flow; that is, for every bounded and uniformly continuous function f on
![]() $T^1M$
, we have
$T^1M$
, we have
Proof. We first observe that the set
![]() $U^1$
of rank 1 vectors in U is open in H, because the set of rank 1 vectors is open in
$U^1$
of rank 1 vectors in U is open in H, because the set of rank 1 vectors is open in
![]() $T^1 \tilde {M}$
[Reference Ballmann2]. By Lemma 2.4, the set
$T^1 \tilde {M}$
[Reference Ballmann2]. By Lemma 2.4, the set
![]() $U^1$
has full measure in U, so the averages on the two sets are the same. Next, we use the fact that
$U^1$
has full measure in U, so the averages on the two sets are the same. Next, we use the fact that
![]() $\mu _H$
is a Radon measure: given a number
$\mu _H$
is a Radon measure: given a number
![]() $\varepsilon>0$
, there exists a compact subset
$\varepsilon>0$
, there exists a compact subset
![]() $K\subset U^1$
such that
$K\subset U^1$
such that
![]() $\mu _H(U^1\setminus K)<\varepsilon $
.
$\mu _H(U^1\setminus K)<\varepsilon $
.
Since
![]() $\Omega $
is closed,
$\Omega $
is closed,
![]() $L=K\cap \Omega $
is again compact, and L has full measure in K, because vectors outside of
$L=K\cap \Omega $
is again compact, and L has full measure in K, because vectors outside of
![]() $\Omega $
are not in the support. We want to show that L is equidistributed. Proposition 2.2 gives an equidistributed open neighborhood
$\Omega $
are not in the support. We want to show that L is equidistributed. Proposition 2.2 gives an equidistributed open neighborhood
![]() $U_v$
of each vector v in L. The set L can be covered by finitely many
$U_v$
of each vector v in L. The set L can be covered by finitely many
![]() $U_v$
because it is compact. We can cut these sets where they intersect to obtain a family
$U_v$
because it is compact. We can cut these sets where they intersect to obtain a family
![]() $\{V_i\}_{1\le i\le n}$
of equidistributed pairwise disjoint Borel sets whose union contains L, thanks to the fact that the subsets of
$\{V_i\}_{1\le i\le n}$
of equidistributed pairwise disjoint Borel sets whose union contains L, thanks to the fact that the subsets of
![]() $U_v$
are equidistributed too.
$U_v$
are equidistributed too.
If we let
![]() $\lambda :=\int f\, \mathrm {d} \mu /\mu (T^1 M)$
, the set
$\lambda :=\int f\, \mathrm {d} \mu /\mu (T^1 M)$
, the set
![]() $V:=V_1\cup \cdots \cup V_n$
is equidistributed because
$V:=V_1\cup \cdots \cup V_n$
is equidistributed because
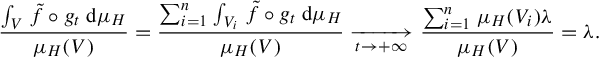 $$ \begin{align*} \frac{\int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H}}{\mu_{H}(V)} =\frac{\sum_{i=1}^n \int_{V_i} \tilde{f}\circ g_t \, \mathrm{d} \mu_{H}}{\mu_{H}(V)} \xrightarrow[t \to +\infty]{} \frac{\sum_{i=1}^n \mu_H(V_i) \lambda}{\mu_H(V)} =\lambda. \end{align*} $$
$$ \begin{align*} \frac{\int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H}}{\mu_{H}(V)} =\frac{\sum_{i=1}^n \int_{V_i} \tilde{f}\circ g_t \, \mathrm{d} \mu_{H}}{\mu_{H}(V)} \xrightarrow[t \to +\infty]{} \frac{\sum_{i=1}^n \mu_H(V_i) \lambda}{\mu_H(V)} =\lambda. \end{align*} $$
On the other hand, we have
![]() $\mu _{H}(U\setminus V)<\varepsilon $
, so
$\mu _{H}(U\setminus V)<\varepsilon $
, so
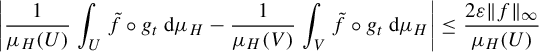 $$ \begin{align*} \bigg| \frac{1}{\mu_{H}(U)}\int_{U} \tilde{f}\circ g_t \, \mathrm{d} \mu_{H} - \frac{1}{\mu_{H}(V)}\int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H} \bigg| \le \frac{2\varepsilon \lVert f \rVert_\infty}{\mu_H(U)} \end{align*} $$
$$ \begin{align*} \bigg| \frac{1}{\mu_{H}(U)}\int_{U} \tilde{f}\circ g_t \, \mathrm{d} \mu_{H} - \frac{1}{\mu_{H}(V)}\int_V \tilde{f}\circ g_t \, \mathrm{d} \mu_{H} \bigg| \le \frac{2\varepsilon \lVert f \rVert_\infty}{\mu_H(U)} \end{align*} $$
for all
![]() $t\ge 0$
. This proves that U is equidistributed as well.
$t\ge 0$
. This proves that U is equidistributed as well.
3 Unique ergodicity of the horocyclic flow
3.1 Surfaces with non-positive curvature
In the second part of this paper we restrict our attention to surfaces. Our goal is to define a flow that preserves the Bowen–Margulis measure and whose orbits are horocycles. Then we would like to interpret the equidistribution of horocycles in terms of the ergodic properties of this flow. The idea is to define the parametrization of the flow by the measures on the horocycles as in the negative curvature case [Reference Marcus15]. However, the presence of flat pieces of horocycle makes it impossible to define globally a continuous flow with this method. We have found a subset
![]() ${\Sigma }$
of the unitary tangent bundle which excludes the horocycles causing trouble, like that of Figure 1, and which is topologically and metrically large. We will define a parametrization of the horocyclic flow on
${\Sigma }$
of the unitary tangent bundle which excludes the horocycles causing trouble, like that of Figure 1, and which is topologically and metrically large. We will define a parametrization of the horocyclic flow on
![]() ${\Sigma }$
and prove that it is uniquely ergodic.
${\Sigma }$
and prove that it is uniquely ergodic.
In this section, M is a non-positively curved non-elementary orientable surface with a closed rank 1 geodesic and the Bowen–Margulis measure
![]() $\mu $
, constructed as before, is assumed to be finite. We will further assume that M satisfies the duality condition, which means that every vector of
$\mu $
, constructed as before, is assumed to be finite. We will further assume that M satisfies the duality condition, which means that every vector of
![]() $T^1M$
is non-wandering, or equivalently we assume that
$T^1M$
is non-wandering, or equivalently we assume that
![]() $\Lambda (\Gamma )=\partial \tilde {M}$
. Under these hypotheses, the geodesic flow is topologically mixing [Reference Eberlein7, Theorem 6.3], so it is also mixing with respect to the Bowen–Margulis measure. The duality condition is satisfied if M has finite Riemannian volume, as an application of the Poincaré recurrence theorem. We observe that a non-positively curved non-elementary rank 1 manifold satisfying the duality condition automatically contains a closed rank 1 geodesic.
$\Lambda (\Gamma )=\partial \tilde {M}$
. Under these hypotheses, the geodesic flow is topologically mixing [Reference Eberlein7, Theorem 6.3], so it is also mixing with respect to the Bowen–Margulis measure. The duality condition is satisfied if M has finite Riemannian volume, as an application of the Poincaré recurrence theorem. We observe that a non-positively curved non-elementary rank 1 manifold satisfying the duality condition automatically contains a closed rank 1 geodesic.
Moreover, we know that any two distinct points on the boundary at infinity can be connected by a geodesic. This follows from the fact that, for a non-flat surface M with the duality condition, the universal cover
![]() $\tilde {M}$
satisfies the visibility axiom [Reference Eberlein8, Proposition 2.5]. Therefore, the map P is surjective.
$\tilde {M}$
satisfies the visibility axiom [Reference Eberlein8, Proposition 2.5]. Therefore, the map P is surjective.
We notice that an orientation of the boundary at infinity
![]() $\partial \tilde {M}$
induces an orientation to each horocycle in
$\partial \tilde {M}$
induces an orientation to each horocycle in
![]() $\mathcal {H}$
. One vector
$\mathcal {H}$
. One vector
![]() $v\in T^1 \tilde {M}$
divides its horocycle
$v\in T^1 \tilde {M}$
divides its horocycle
![]() $H^u(v)$
into two connected sets, one in the positively oriented direction,
$H^u(v)$
into two connected sets, one in the positively oriented direction,
![]() $H^u_+(v)$
, and the other in the negatively oriented direction,
$H^u_+(v)$
, and the other in the negatively oriented direction,
![]() $H^u_-(v)$
. The group of isometries
$H^u_-(v)$
. The group of isometries
![]() $\Gamma $
is orientation-preserving because M is orientable. In consequence, horocycles on
$\Gamma $
is orientation-preserving because M is orientable. In consequence, horocycles on
![]() $T^1\tilde {M}$
descend to
$T^1\tilde {M}$
descend to
![]() $T^1M$
as oriented immersed curves.
$T^1M$
as oriented immersed curves.
Horocycles are diffeomorphic to the real line. Let H be a horocycle of
![]() $T^1 \tilde {M}$
. The interval
$T^1 \tilde {M}$
. The interval
![]() $(v,w)\subset H$
between two vectors
$(v,w)\subset H$
between two vectors
![]() $v,w\in H$
is the connected subset bounded by v and w. The map
$v,w\in H$
is the connected subset bounded by v and w. The map
![]() $P_H:H\rightarrow \partial \tilde {M}\setminus \{\xi \}$
, where
$P_H:H\rightarrow \partial \tilde {M}\setminus \{\xi \}$
, where
![]() $\xi $
is the center of H, which projects a vector to its positive endpoint, is continuous and surjective. We also observe that
$\xi $
is the center of H, which projects a vector to its positive endpoint, is continuous and surjective. We also observe that
![]() $P_H(v)=P_H(w)$
, with
$P_H(v)=P_H(w)$
, with
![]() $v\not =w$
, implies, according to the flat strip theorem, that the curvature vanishes on the strip
$v\not =w$
, implies, according to the flat strip theorem, that the curvature vanishes on the strip
![]() $\pi (\cup _{t\in \mathbb {R}} g_t((v,w)))$
. Such an interval
$\pi (\cup _{t\in \mathbb {R}} g_t((v,w)))$
. Such an interval
![]() $(v,w)$
will be called a flat piece of horocycle (see Figure 4). It is clear that H does not contain any flat piece if and only if
$(v,w)$
will be called a flat piece of horocycle (see Figure 4). It is clear that H does not contain any flat piece if and only if
![]() $P_H$
is injective, in which case
$P_H$
is injective, in which case
![]() $P_H$
is also a homeomorphism.
$P_H$
is also a homeomorphism.
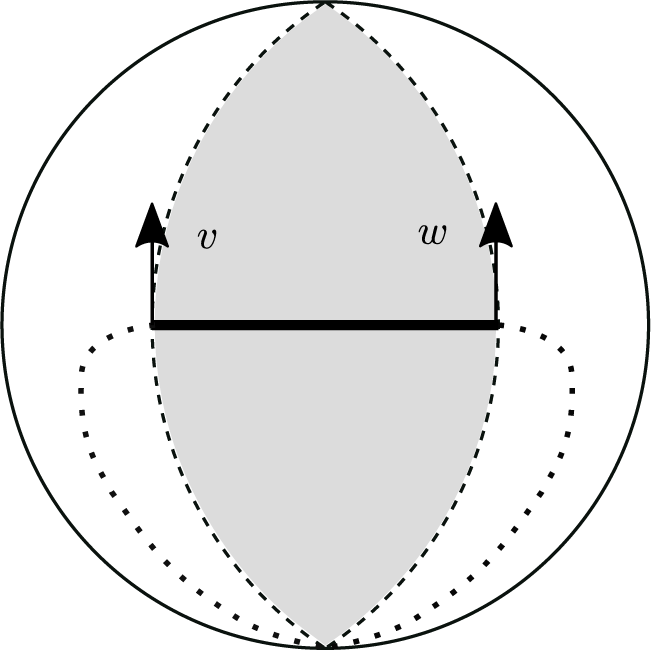
Figure 4 Universal cover of the surface
![]() ${M}$
with a region where the curvature vanishes (shaded region). We represent an unstable horocycle with a flat piece.
${M}$
with a region where the curvature vanishes (shaded region). We represent an unstable horocycle with a flat piece.
3.2 Definition of the horocyclic flow on a certain subset of
 $T^1 M$
$T^1 M$
Next, we define a subset of the unitary tangent bundle
![]() $T^1 \tilde {M}$
of
$T^1 \tilde {M}$
of
![]() $\tilde {M}$
and we study the properties of its horocycles and their associated measures. Let
$\tilde {M}$
and we study the properties of its horocycles and their associated measures. Let
![]() $\tilde {\Sigma } \subset T^1\tilde {M}$
denote the set of vectors whose horocycle contains a rank 1 recurrent vector, that is to say,
$\tilde {\Sigma } \subset T^1\tilde {M}$
denote the set of vectors whose horocycle contains a rank 1 recurrent vector, that is to say,
This set is invariant under
![]() $\Gamma $
, under the geodesic flow and under the horocyclic foliation, in the sense that
$\Gamma $
, under the geodesic flow and under the horocyclic foliation, in the sense that
![]() $\tilde {\Sigma }$
contains a horocycle H as soon as it contains one vector of H. Our set
$\tilde {\Sigma }$
contains a horocycle H as soon as it contains one vector of H. Our set
![]() $\tilde {\Sigma }$
contains a
$\tilde {\Sigma }$
contains a
![]() $G_\delta $
-dense set, namely the set of rank 1 recurrent vectors
$G_\delta $
-dense set, namely the set of rank 1 recurrent vectors
![]() $Rec^1$
. The latter is the intersection of the set of rank 1 vectors, which is open and dense [Reference Ballmann2, Corollary III.3.8], with the set of recurrent vectors, which is
$Rec^1$
. The latter is the intersection of the set of rank 1 vectors, which is open and dense [Reference Ballmann2, Corollary III.3.8], with the set of recurrent vectors, which is
![]() $G_\delta $
-dense when all the vectors of
$G_\delta $
-dense when all the vectors of
![]() $T^1M$
are non-wandering. The set
$T^1M$
are non-wandering. The set
![]() $\tilde {\Sigma }$
also has full
$\tilde {\Sigma }$
also has full
![]() $\mu $
-measure. By Lemma 2.3, all the vectors in
$\mu $
-measure. By Lemma 2.3, all the vectors in
![]() $\tilde {\Sigma }$
have rank 1 and each horocycle
$\tilde {\Sigma }$
have rank 1 and each horocycle
![]() $H\subset \tilde {\Sigma }$
coincides with the unstable manifold. This also implies that the horocycles in
$H\subset \tilde {\Sigma }$
coincides with the unstable manifold. This also implies that the horocycles in
![]() $\tilde {\Sigma } $
do not contain any flat pieces of horocycle.
$\tilde {\Sigma } $
do not contain any flat pieces of horocycle.
In the next lemma, which will be needed later, we prove a sort of continuity of the measures on the horocycles contained in
![]() $\tilde {\Sigma }$
.
$\tilde {\Sigma }$
.
Lemma 3.1. The map
 $$ \begin{align*} \begin{matrix} \{(v,w)\in \tilde{\Sigma}\times \tilde{\Sigma}\,|\,w\in H^u(v)\} & \longrightarrow & \mathbb{R} \\ (v,w) & \longmapsto & \mu_{H^u(v)}((v,w)) \end{matrix} \end{align*} $$
$$ \begin{align*} \begin{matrix} \{(v,w)\in \tilde{\Sigma}\times \tilde{\Sigma}\,|\,w\in H^u(v)\} & \longrightarrow & \mathbb{R} \\ (v,w) & \longmapsto & \mu_{H^u(v)}((v,w)) \end{matrix} \end{align*} $$
is continuous.
Proof. Let v and w be two points in
![]() $\tilde {\Sigma }$
sharing a horocycle. The function on a pair of points
$\tilde {\Sigma }$
sharing a horocycle. The function on a pair of points
![]() $(v',w')$
close to
$(v',w')$
close to
![]() $(v,w)$
can be written as the integral
$(v,w)$
can be written as the integral
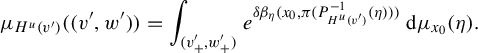 $$ \begin{align*} \mu_{H^u(v')}((v',w'))=\int_{(v^{\prime}_+,w^{\prime}_+)}e^{\delta \beta_\eta (x_0,\pi(P^{-1}_{H^u(v')}(\eta)))}\, \mathrm{d} \mu_{x_0}(\eta). \end{align*} $$
$$ \begin{align*} \mu_{H^u(v')}((v',w'))=\int_{(v^{\prime}_+,w^{\prime}_+)}e^{\delta \beta_\eta (x_0,\pi(P^{-1}_{H^u(v')}(\eta)))}\, \mathrm{d} \mu_{x_0}(\eta). \end{align*} $$
Given
![]() $\varepsilon>0$
, we can suppose that
$\varepsilon>0$
, we can suppose that
![]() $\mu _{x_0}((v^{\prime }_+,w^{\prime }_+)\triangle (v_+,w_+))<\varepsilon $
. We estimate the Busemann cocycles on
$\mu _{x_0}((v^{\prime }_+,w^{\prime }_+)\triangle (v_+,w_+))<\varepsilon $
. We estimate the Busemann cocycles on
![]() $H^u(v)$
and
$H^u(v)$
and
![]() $H^u(v')$
as we did in the proof of Proposition 2.2: for all
$H^u(v')$
as we did in the proof of Proposition 2.2: for all
![]() $\eta \in (v_+,w_+)$
we have
$\eta \in (v_+,w_+)$
we have
provided that
![]() $v'$
is close to v. We also observe that
$v'$
is close to v. We also observe that
![]() $\exp ({\delta \beta _\eta (x_0,\,\pi (P^{-1}_{H^u(v')}(\eta )))})$
is bounded by a constant K for
$\exp ({\delta \beta _\eta (x_0,\,\pi (P^{-1}_{H^u(v')}(\eta )))})$
is bounded by a constant K for
![]() $v'$
in a neighborhood of v and
$v'$
in a neighborhood of v and
![]() $\eta $
in a neighborhood of
$\eta $
in a neighborhood of
![]() $v_+$
or
$v_+$
or
![]() $w_+$
. With these approximations we get the inequalities
$w_+$
. With these approximations we get the inequalities
which show the continuity at
![]() $(v,w)$
.
$(v,w)$
.
Let us remark that only the fact that all the vectors in the domain
![]() $\tilde {\Sigma }$
have rank 1 was used in the previous proof. Next, we state and prove some properties of individual measures on horocycles that will help later to define the parametrization.
$\tilde {\Sigma }$
have rank 1 was used in the previous proof. Next, we state and prove some properties of individual measures on horocycles that will help later to define the parametrization.
Lemma 3.2. Let H be a horocycle of
![]() $T^1\tilde {M}$
and
$T^1\tilde {M}$
and
![]() $v\in H$
:
$v\in H$
:
-
(i) the measure
 $\mu _H$
has no point masses;
$\mu _H$
has no point masses; -
(ii) if H does not contain a flat piece, then
 $\mu _H$
is of full support in H;
$\mu _H$
is of full support in H; -
(iii) the measure
 $\mu _H$
is finite on compact sets;
$\mu _H$
is finite on compact sets; -
(iv) if v is in
 $\tilde {\Sigma }$
, then the half-horospheres
$\tilde {\Sigma }$
, then the half-horospheres
 $H^u_+(v)$
and
$H^u_+(v)$
and
 $H^u_-(v)$
have infinite measure.
$H^u_-(v)$
have infinite measure.
Proof. (i) We know that
![]() $\mu _{x_0}$
has no point masses. If
$\mu _{x_0}$
has no point masses. If
![]() $w\in H$
, then
$w\in H$
, then
![]() $\mu _{x_0}(\{v_+\})=0$
directly implies that
$\mu _{x_0}(\{v_+\})=0$
directly implies that
![]() $\mu _H(\{v\})=0$
.
$\mu _H(\{v\})=0$
.
(ii) If
![]() $U\subset H$
is an open non-empty subset,
$U\subset H$
is an open non-empty subset,
![]() $P_H(U)$
is also open and non-empty. So
$P_H(U)$
is also open and non-empty. So
![]() $\mu _{x_0}(P_H(U))>0$
because its support is
$\mu _{x_0}(P_H(U))>0$
because its support is
![]() $\Lambda (\Gamma )=\partial \tilde {M}$
. Then
$\Lambda (\Gamma )=\partial \tilde {M}$
. Then
![]() $\mu _H(U)=\int _{P_H(U)}\phi _v \mathrm {d} \mu _{x_0}>0$
.
$\mu _H(U)=\int _{P_H(U)}\phi _v \mathrm {d} \mu _{x_0}>0$
.
(iii) If
![]() $K\subset H$
is compact,
$K\subset H$
is compact,
![]() $P_H(K)$
is also compact. The function
$P_H(K)$
is also compact. The function
![]() $\phi _v$
is bounded on
$\phi _v$
is bounded on
![]() $P_H(K)$
. The volume part of the integral is bounded by the length of K. Then it is clear that
$P_H(K)$
. The volume part of the integral is bounded by the length of K. Then it is clear that
![]() $\mu _H(K)$
is finite.
$\mu _H(K)$
is finite.
(iv) By (iii) it is clear that, for every
![]() $w\in H^u(v)$
, the measure of
$w\in H^u(v)$
, the measure of
![]() $H^u_+(v)$
is infinite if and only if so is the measure of
$H^u_+(v)$
is infinite if and only if so is the measure of
![]() $H^u_+(w)$
. So we can assume that v is in
$H^u_+(w)$
. So we can assume that v is in
![]() $Rec^1$
.
$Rec^1$
.
Let
![]() $B^u(w,r)$
denote the open ball in
$B^u(w,r)$
denote the open ball in
![]() $H^u(w)$
of center w and radius
$H^u(w)$
of center w and radius
![]() $r>0$
. The balls
$r>0$
. The balls
![]() $B^u(w,1)$
have two boundary points
$B^u(w,1)$
have two boundary points
![]() $a_w,b_w\in H^u(w)$
that depend continuously on w so that
$a_w,b_w\in H^u(w)$
that depend continuously on w so that
![]() $B^u(w,1)=(a_w,b_w)$
. In view of Lemma 3.1, the function
$B^u(w,1)=(a_w,b_w)$
. In view of Lemma 3.1, the function
![]() $w\mapsto \mu _{H^u(w)}((a_w,w))$
is continuous. The continuity at v implies that there exists a neighborhood U of v in
$w\mapsto \mu _{H^u(w)}((a_w,w))$
is continuous. The continuity at v implies that there exists a neighborhood U of v in
![]() $\tilde {\Sigma }$
such that, for all
$\tilde {\Sigma }$
such that, for all
![]() $w\in U$
,
$w\in U$
,
The inequality is in fact valid on
![]() $\cup _{\gamma \in \Gamma } \gamma U$
because the family of measures is
$\cup _{\gamma \in \Gamma } \gamma U$
because the family of measures is
![]() $\Gamma $
-invariant.
$\Gamma $
-invariant.
Since v is recurrent, there are a sequence
![]() $t_k$
converging to
$t_k$
converging to
![]() $-\infty $
and isometries
$-\infty $
and isometries
![]() $\gamma _k \in \Gamma $
such that the distance
$\gamma _k \in \Gamma $
such that the distance
![]() $d_1(g_{t_k}v, \gamma _k v)$
goes to
$d_1(g_{t_k}v, \gamma _k v)$
goes to
![]() $0$
. For k big enough, the vector
$0$
. For k big enough, the vector
![]() $g_{t_k}v$
is in
$g_{t_k}v$
is in
![]() $\gamma _k U$
, so equation (3) remains true if we replace w by
$\gamma _k U$
, so equation (3) remains true if we replace w by
![]() $g_{t_k}v$
. Let
$g_{t_k}v$
. Let
![]() $a_k, b_k$
be the points in
$a_k, b_k$
be the points in
![]() $H^u(g_{t_k}v)$
such that
$H^u(g_{t_k}v)$
such that
![]() $B^u(g_{t_k}v,1)=(a_k,b_k)$
. Using the fact that the measures on horocycles expand exponentially, we obtain
$B^u(g_{t_k}v,1)=(a_k,b_k)$
. Using the fact that the measures on horocycles expand exponentially, we obtain
This shows that in one half-horocycle there are subsets of arbitrarily large measure. We proceed analogously for the other half-horocycle, with
![]() $b_k$
instead of
$b_k$
instead of
![]() $a_k$
.
$a_k$
.
We can now define a suitable parametrization of the horocyclic flow on the set
![]() $\tilde {\Sigma }$
. Given
$\tilde {\Sigma }$
. Given
![]() $v\in \tilde {\Sigma }$
, we consider the function
$v\in \tilde {\Sigma }$
, we consider the function
![]() $m_v:H^u_+(v)\rightarrow (0,+\infty )$
defined by
$m_v:H^u_+(v)\rightarrow (0,+\infty )$
defined by
![]() $m_v(w):=\mu _{H^u(v)}((v,w))$
. The map
$m_v(w):=\mu _{H^u(v)}((v,w))$
. The map
![]() $m_v$
is well defined by properties (ii) and (iii) of Lemma 3.2, is continuous by (i), strictly increasing (with the order given by the orientation) by (ii) and surjective by (iv). Then
$m_v$
is well defined by properties (ii) and (iii) of Lemma 3.2, is continuous by (i), strictly increasing (with the order given by the orientation) by (ii) and surjective by (iv). Then
![]() $m_v$
is in fact a homeomorphism, because the domain and the codomain of the function are topologically the real line. For
$m_v$
is in fact a homeomorphism, because the domain and the codomain of the function are topologically the real line. For
![]() $s>0$
, we set
$s>0$
, we set
![]() $h_s(v)=m_v^{-1}(s)$
, so that the measure of the interval
$h_s(v)=m_v^{-1}(s)$
, so that the measure of the interval
![]() $(v,h_s(v))$
is s. There is a similar map on the negative half-horocycle
$(v,h_s(v))$
is s. There is a similar map on the negative half-horocycle
![]() $H^u_-(v)$
that allows us to define the flow
$H^u_-(v)$
that allows us to define the flow
![]() $h_s(v)$
for negative time, and we also set the obvious relation
$h_s(v)$
for negative time, and we also set the obvious relation
![]() $h_0(v)=v$
.
$h_0(v)=v$
.
It is clear that the flow satisfies the group law,
![]() $h_{s_1}\circ h_{s_2}=h_{s_1+s_2}$
, because of the additivity of the measure and property (i). For the same reasons, the measure of every interval
$h_{s_1}\circ h_{s_2}=h_{s_1+s_2}$
, because of the additivity of the measure and property (i). For the same reasons, the measure of every interval
![]() $I\subset H^u(v)$
(hence, every measurable set) is preserved,
$I\subset H^u(v)$
(hence, every measurable set) is preserved,
![]() $\mu _{H^u(v)}(h_s(I))=\mu _{H^u(v)}(I)$
. Thanks to the product structure of the measure (equation (2)), we deduce that
$\mu _{H^u(v)}(h_s(I))=\mu _{H^u(v)}(I)$
. Thanks to the product structure of the measure (equation (2)), we deduce that
![]() $h_s$
preserves
$h_s$
preserves
![]() $\mu $
. The expanding property of the measures on horocycles is transformed into the commutation relation
$\mu $
. The expanding property of the measures on horocycles is transformed into the commutation relation
![]() $g_t\circ h_s = h_{se^{\delta t}} \circ g_t $
between the geodesic flow and the horocyclic flow. Only the continuity of
$g_t\circ h_s = h_{se^{\delta t}} \circ g_t $
between the geodesic flow and the horocyclic flow. Only the continuity of
![]() $h_s$
remains to be proved.
$h_s$
remains to be proved.
Lemma 3.3. The flow
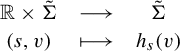 $$ \begin{align*} \begin{matrix} \mathbb{R}\times \tilde{\Sigma} & \longrightarrow & \tilde{\Sigma} \\ (s,v) & \longmapsto & h_s(v) \end{matrix} \end{align*} $$
$$ \begin{align*} \begin{matrix} \mathbb{R}\times \tilde{\Sigma} & \longrightarrow & \tilde{\Sigma} \\ (s,v) & \longmapsto & h_s(v) \end{matrix} \end{align*} $$
is continuous.
Proof. Let
![]() $s\in \mathbb {R}$
and
$s\in \mathbb {R}$
and
![]() $v\in \tilde {\Sigma }$
and consider sequences
$v\in \tilde {\Sigma }$
and consider sequences
![]() $s_k\to s$
and
$s_k\to s$
and
![]() $v_k \to v$
. We know that the horocycles
$v_k \to v$
. We know that the horocycles
![]() $H^u(w)$
depend continuously on w, so for each k there exists a vector
$H^u(w)$
depend continuously on w, so for each k there exists a vector
![]() $w_k\in H^u(v_k)$
such that the sequence
$w_k\in H^u(v_k)$
such that the sequence
![]() $\{w_k\}_k$
converges to
$\{w_k\}_k$
converges to
![]() $h_s(v)$
. By Lemma 3.1, we have
$h_s(v)$
. By Lemma 3.1, we have
![]() $\mu _{H^u(v_k)}((v_k,w_k))\to \mu _{H^u(v)}((v,h_s(v)))=|s|$
. We deduce then that the measures of the intervals
$\mu _{H^u(v_k)}((v_k,w_k))\to \mu _{H^u(v)}((v,h_s(v)))=|s|$
. We deduce then that the measures of the intervals
![]() $(w_k,h_{s_k}(v_k))$
tend to
$(w_k,h_{s_k}(v_k))$
tend to
![]() $0$
. If the distance between
$0$
. If the distance between
![]() $w_k$
and
$w_k$
and
![]() $h_{s_k}(v_k)$
tends to
$h_{s_k}(v_k)$
tends to
![]() $0$
too, then we obtain
$0$
too, then we obtain
![]() $h_{s_k}(v_k)\to h_s(v)$
so the flow is continuous at
$h_{s_k}(v_k)\to h_s(v)$
so the flow is continuous at
![]() $(s,v)$
.
$(s,v)$
.
Otherwise, we get a contradiction. To see this, suppose that, for some
![]() $\varepsilon>0$
and subsequence
$\varepsilon>0$
and subsequence
![]() $k_i$
, the Riemannian distance
$k_i$
, the Riemannian distance
![]() $d_1(w_{k_i},h_{s_{k_i}}(v_{k_i}))$
is greater than
$d_1(w_{k_i},h_{s_{k_i}}(v_{k_i}))$
is greater than
![]() $\varepsilon $
. Then, since
$\varepsilon $
. Then, since
![]() $w_{k_i}\to h_s(v)$
, for i big enough
$w_{k_i}\to h_s(v)$
, for i big enough
![]() $h_{s_{k_i}}(v_{k_i})$
is at distance greater than
$h_{s_{k_i}}(v_{k_i})$
is at distance greater than
![]() $\varepsilon /2$
from
$\varepsilon /2$
from
![]() $h_s(v)$
. But the sequence
$h_s(v)$
. But the sequence
![]() $h_{s_{k_i}}(v_{k_i})$
must accumulate at some point
$h_{s_{k_i}}(v_{k_i})$
must accumulate at some point
![]() $\zeta $
in
$\zeta $
in
![]() $H^u(v)\cup \{v_-\}$
, outside of a ball centered at
$H^u(v)\cup \{v_-\}$
, outside of a ball centered at
![]() $h_s(v)$
. Again by the continuity of the measure, it follows that
$h_s(v)$
. Again by the continuity of the measure, it follows that
![]() $\mu _{H^u(v)}((h_s(v),\zeta ))=0$
, which is impossible because the interval is non-empty.
$\mu _{H^u(v)}((h_s(v),\zeta ))=0$
, which is impossible because the interval is non-empty.
3.3 Unique ergodicity of the horocyclic flow on
 $\Sigma $
$\Sigma $
To study the ergodic properties of the horocyclic flow we introduce the Birkhoff averages. Let
![]() $f:T^1M \rightarrow \mathbb {R}$
be a Borel function and
$f:T^1M \rightarrow \mathbb {R}$
be a Borel function and
![]() $\tilde {f}:T^1\tilde {M}\rightarrow \mathbb {R}$
its lift. For a number
$\tilde {f}:T^1\tilde {M}\rightarrow \mathbb {R}$
its lift. For a number
![]() $R>0$
and v in
$R>0$
and v in
![]() $\tilde {\Sigma }$
, we define
$\tilde {\Sigma }$
, we define
 $$ \begin{align*} M_R(f)(v):=\frac{1}{R}\int_0^R\tilde{f}(h_s(v))\,\mathrm{d}s. \end{align*} $$
$$ \begin{align*} M_R(f)(v):=\frac{1}{R}\int_0^R\tilde{f}(h_s(v))\,\mathrm{d}s. \end{align*} $$
A simple computation using the commutation relation between the geodesic and the horocyclic flow shows that
![]() $M_R(f\circ g_t)=M_{Re^{\delta t}}(f)\circ g_t$
.
$M_R(f\circ g_t)=M_{Re^{\delta t}}(f)\circ g_t$
.
Moreover, if we suppose that f is bounded and uniformly continuous, the equidistribution under the action of the geodesic flow we showed in Theorem A implies that the Birkhoff averages
![]() $M_1(f\circ g_t)$
converge pointwise to
$M_1(f\circ g_t)$
converge pointwise to
![]() $\int f \,\mathrm {d} \mu /\mu (T^1 M)$
when the time t goes to
$\int f \,\mathrm {d} \mu /\mu (T^1 M)$
when the time t goes to
![]() $+\infty $
. However, we need to understand the behavior of
$+\infty $
. However, we need to understand the behavior of
![]() $M_R(f)$
when R goes to infinity, that is to say, the equidistribution of horocycles in length. To do this we will use the relation
$M_R(f)$
when R goes to infinity, that is to say, the equidistribution of horocycles in length. To do this we will use the relation
![]() $M_1(f\circ g_t)=M_{e^{\delta t}}(f)\circ g_t$
and some kind of uniform convergence of the averages
$M_1(f\circ g_t)=M_{e^{\delta t}}(f)\circ g_t$
and some kind of uniform convergence of the averages
![]() $M_1(f\circ g_t)$
towards the average of f on the unitary tangent bundle of the manifold M, which we will prove.
$M_1(f\circ g_t)$
towards the average of f on the unitary tangent bundle of the manifold M, which we will prove.
It is clear from the continuity of the measures on horocycles (Lemma 3.1) that the function
![]() $M_1(f\circ g_t)$
is continuous on
$M_1(f\circ g_t)$
is continuous on
![]() $\tilde {\Sigma }$
. We can prove the following improved result.
$\tilde {\Sigma }$
. We can prove the following improved result.
Proposition 3.4. Let M be an orientable rank 1 complete connected Riemannian surface with non-positive curvature satisfying the duality condition. Let f be a bounded and uniformly continuous function on
![]() $T^1M$
. Then the family of functions
$T^1M$
. Then the family of functions
![]() $\{M_1(f\circ g_t)\}_{t>0} $
is equicontinuous at every vector of
$\{M_1(f\circ g_t)\}_{t>0} $
is equicontinuous at every vector of
![]() $\tilde {\Sigma }$
.
$\tilde {\Sigma }$
.
Proof. Let v be a vector in
![]() $\tilde {\Sigma }$
. The average of the horocyclic flow can be written explicitly as
$\tilde {\Sigma }$
. The average of the horocyclic flow can be written explicitly as
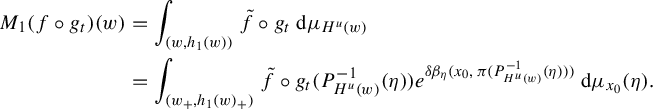 $$ \begin{align} M_1(f\circ g_t)(w)&=\int_{(w,h_1(w))}\tilde{f} \circ g_t \,\mathrm{d} \mu_{H^u(w)}\nonumber\\ &= \int_{(w_+,h_1(w)_+)} \tilde{f} \circ g_t (P_{H^u(w)}^{-1}(\eta)) e^{\delta \beta_\eta(x_0,\,\pi(P_{H^u(w)}^{-1}(\eta)))}\, \mathrm{d} \mu_{x_0}(\eta). \end{align} $$
$$ \begin{align} M_1(f\circ g_t)(w)&=\int_{(w,h_1(w))}\tilde{f} \circ g_t \,\mathrm{d} \mu_{H^u(w)}\nonumber\\ &= \int_{(w_+,h_1(w)_+)} \tilde{f} \circ g_t (P_{H^u(w)}^{-1}(\eta)) e^{\delta \beta_\eta(x_0,\,\pi(P_{H^u(w)}^{-1}(\eta)))}\, \mathrm{d} \mu_{x_0}(\eta). \end{align} $$
Fix
![]() $\varepsilon>0$
. We consider a relatively compact neighborhood U of v such that, for all
$\varepsilon>0$
. We consider a relatively compact neighborhood U of v such that, for all
![]() $w\in U$
,
$w\in U$
,
Let C be a uniform bound of
![]() $\exp ({\delta \beta _\eta (x_0,\,P_{H^u(w)}^{-1}(\eta ))})$
for
$\exp ({\delta \beta _\eta (x_0,\,P_{H^u(w)}^{-1}(\eta ))})$
for
![]() $w\in U$
and
$w\in U$
and
![]() $\eta $
in a compact neighborhood of
$\eta $
in a compact neighborhood of
![]() $\overline {(v_+,h_1(v)_+)}$
. When w approaches v, the set
$\overline {(v_+,h_1(v)_+)}$
. When w approaches v, the set
![]() $(w_+,h_1(w)_+)$
will be contained in this compact neighborhood. Then we can change the domain of integration in equation (4) to
$(w_+,h_1(w)_+)$
will be contained in this compact neighborhood. Then we can change the domain of integration in equation (4) to
![]() $(v_+,h_1(v)_+)$
with an error of
$(v_+,h_1(v)_+)$
with an error of
![]() $\varepsilon \lVert f \rVert _\infty C$
at most.
$\varepsilon \lVert f \rVert _\infty C$
at most.
By the uniform continuity of
![]() $\tilde {f}$
, there is a number
$\tilde {f}$
, there is a number
![]() $r>0$
such that
$r>0$
such that
![]() $|\tilde {f}(w)-\tilde {f}(w')|<\varepsilon $
if
$|\tilde {f}(w)-\tilde {f}(w')|<\varepsilon $
if
![]() $d_1(w,w')<r$
. If w is close enough to v, for all
$d_1(w,w')<r$
. If w is close enough to v, for all
![]() $\eta \in (v_+,h_1(v)_+)$
,
$\eta \in (v_+,h_1(v)_+)$
,
![]() $P_{H^u(w)}^{-1} (\eta )$
is at distance less than r from
$P_{H^u(w)}^{-1} (\eta )$
is at distance less than r from
![]() $ P_{H^u(v)}^{-1}(\eta )$
. Applying the geodesic flow
$ P_{H^u(v)}^{-1}(\eta )$
. Applying the geodesic flow
![]() $g_t$
,
$g_t$
,
![]() $t\ge 0$
to these two vectors, their distance does not increase. Hence, when w is close to v,
$t\ge 0$
to these two vectors, their distance does not increase. Hence, when w is close to v,
This is essentially the same we did in property (ii) of the proof of Proposition 2.2. If we consider a w close enough to v we can also control the difference between
![]() $\exp ({\delta \beta _\eta (x_0,\,P_{H^u(w)}^{-1}(\eta ))})$
and
$\exp ({\delta \beta _\eta (x_0,\,P_{H^u(w)}^{-1}(\eta ))})$
and
![]() $\exp ({\delta \beta _\eta (x_0,\,P_{H^u(v)}^{-1}(\eta ))})$
. So the values of the functions at w are close to the values at v uniformly in t when the two vectors are close. This shows that
$\exp ({\delta \beta _\eta (x_0,\,P_{H^u(v)}^{-1}(\eta ))})$
. So the values of the functions at w are close to the values at v uniformly in t when the two vectors are close. This shows that
![]() $\{M_1(f\circ g_t)\}_{t>0} $
is equicontinuous at v.
$\{M_1(f\circ g_t)\}_{t>0} $
is equicontinuous at v.
We also observe that the function
![]() $M_1(f\circ g_t)$
is bounded by the uniform norm
$M_1(f\circ g_t)$
is bounded by the uniform norm
![]() $\lVert f \rVert _\infty $
. Both the set
$\lVert f \rVert _\infty $
. Both the set
![]() $\tilde {\Sigma }$
and the functions
$\tilde {\Sigma }$
and the functions
![]() $M_R(f):\tilde {\Sigma } \rightarrow \mathbb {R}$
are invariant under
$M_R(f):\tilde {\Sigma } \rightarrow \mathbb {R}$
are invariant under
![]() $\Gamma $
, so they descend respectively to a set
$\Gamma $
, so they descend respectively to a set
![]() $\Sigma \subset T^1 M$
and some functions
$\Sigma \subset T^1 M$
and some functions
![]() $\bar {M}_R(f): \Sigma \rightarrow \mathbb {R}$
. We will apply the Arzelà–Ascoli theorem on the space of continuous functions
$\bar {M}_R(f): \Sigma \rightarrow \mathbb {R}$
. We will apply the Arzelà–Ascoli theorem on the space of continuous functions
![]() $C(K)$
over a compact set
$C(K)$
over a compact set
![]() $K\subset \Sigma $
. For every uniformly continuous and bounded function
$K\subset \Sigma $
. For every uniformly continuous and bounded function
![]() $f:T^1 M\rightarrow \mathbb {R}$
, the family
$f:T^1 M\rightarrow \mathbb {R}$
, the family
![]() $\{\bar {M}_1(f\circ g_t)|_K\}_{t>0} \subset C(K)$
is equicontinuous and uniformly bounded, so it is a relatively compact subset of
$\{\bar {M}_1(f\circ g_t)|_K\}_{t>0} \subset C(K)$
is equicontinuous and uniformly bounded, so it is a relatively compact subset of
![]() $C(K)$
in the uniform convergence topology. This is enough to prove that
$C(K)$
in the uniform convergence topology. This is enough to prove that
![]() $\bar {M}_1(f\circ g_t)|_K$
converges uniformly to
$\bar {M}_1(f\circ g_t)|_K$
converges uniformly to
![]() $\int f \,\mathrm {d} \mu /\mu (T^1M)$
when
$\int f \,\mathrm {d} \mu /\mu (T^1M)$
when
![]() $t\to +\infty $
, or we get a contradiction otherwise. Indeed, if we suppose that there is no uniform convergence, there will exist a constant
$t\to +\infty $
, or we get a contradiction otherwise. Indeed, if we suppose that there is no uniform convergence, there will exist a constant
![]() $\varepsilon>0$
, a sequence
$\varepsilon>0$
, a sequence
![]() $t_n\to +\infty $
and points
$t_n\to +\infty $
and points
![]() $w_n$
in K such that
$w_n$
in K such that
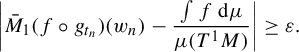 $$ \begin{align} \bigg|\bar{M}_1(f\circ g_{t_n})(w_n)-\frac{\int f\, \mathrm{d} \mu}{\mu(T^1M)} \bigg|\ge \varepsilon. \end{align} $$
$$ \begin{align} \bigg|\bar{M}_1(f\circ g_{t_n})(w_n)-\frac{\int f\, \mathrm{d} \mu}{\mu(T^1M)} \bigg|\ge \varepsilon. \end{align} $$
However, because of the sequential compactness of the closure of
![]() $\{\bar {M}_1(f\circ g_t)|_K\}_{t>0}$
, there exists a subsequence
$\{\bar {M}_1(f\circ g_t)|_K\}_{t>0}$
, there exists a subsequence
![]() $t_{n_k}$
where
$t_{n_k}$
where
![]() $\bar {M}_1(f\circ g_{t_{n_k}})|_K$
converges uniformly to some function
$\bar {M}_1(f\circ g_{t_{n_k}})|_K$
converges uniformly to some function
![]() $\varphi $
in
$\varphi $
in
![]() $C(K)$
. In particular,
$C(K)$
. In particular,
![]() $\bar {M}_1(f\circ g_{t_{n_k}})|_K$
converges pointwise to
$\bar {M}_1(f\circ g_{t_{n_k}})|_K$
converges pointwise to
![]() $\varphi $
, but also to
$\varphi $
, but also to
![]() $\int f \,\mathrm {d} \mu /\mu (T^1M)$
as mentioned above (consequence of Theorem A), so
$\int f \,\mathrm {d} \mu /\mu (T^1M)$
as mentioned above (consequence of Theorem A), so
![]() $\varphi $
is constant and equal to
$\varphi $
is constant and equal to
![]() $\int f \,\mathrm {d} \mu /\mu (T^1M)$
. But
$\int f \,\mathrm {d} \mu /\mu (T^1M)$
. But
![]() $\bar {M}_1(f\circ g_{t_{n_k}})$
converging to
$\bar {M}_1(f\circ g_{t_{n_k}})$
converging to
![]() $\int f \,\mathrm {d} \mu /\mu (T^1M)$
in the uniform norm contradicts equation (5). We have shown the following result.
$\int f \,\mathrm {d} \mu /\mu (T^1M)$
in the uniform norm contradicts equation (5). We have shown the following result.
Proposition 3.5. Let M be an orientable rank 1 complete connected Riemannian surface with non-positive curvature satisfying the duality condition. Assume that the Bowen–Margulis measure
![]() $\mu $
is finite. Let f be a bounded and uniformly continuous function on
$\mu $
is finite. Let f be a bounded and uniformly continuous function on
![]() $T^1M$
. Then the functions
$T^1M$
. Then the functions
![]() $\bar {M}_1(f\circ g_{t}):\Sigma \rightarrow \mathbb {R}$
converge uniformly on compact sets to the constant
$\bar {M}_1(f\circ g_{t}):\Sigma \rightarrow \mathbb {R}$
converge uniformly on compact sets to the constant
![]() $\int f \,\mathrm {d} \mu /\mu (T^1M)$
when the time t tends to
$\int f \,\mathrm {d} \mu /\mu (T^1M)$
when the time t tends to
![]() $+\infty $
.
$+\infty $
.
Finally, we state Theorem B again and prove it with the help of the Birkhoff averages. Recall that
![]() $\Sigma $
is the set of vectors whose horosphere contains a rank 1 recurrent vector, and
$\Sigma $
is the set of vectors whose horosphere contains a rank 1 recurrent vector, and
![]() $\Sigma $
has full
$\Sigma $
has full
![]() $\mu $
-measure in
$\mu $
-measure in
![]() $T^1 M$
.
$T^1 M$
.
Theorem 3.6. Let M be an orientable rank 1 complete connected Riemannian surface with non-positive curvature satisfying the duality condition. Assume that the Bowen–Margulis measure
![]() $\mu $
is finite. Then every finite Borel measure on
$\mu $
is finite. Then every finite Borel measure on
![]() $\Sigma $
invariant under the horocyclic flow
$\Sigma $
invariant under the horocyclic flow
![]() $h_s$
is a constant multiple of the Bowen–Margulis measure
$h_s$
is a constant multiple of the Bowen–Margulis measure
![]() $\mu |_\Sigma $
restricted to
$\mu |_\Sigma $
restricted to
![]() $\Sigma $
.
$\Sigma $
.
Proof. Firstly, let us prove that, for every bounded and uniformly continuous function
![]() $f:T^1 M\rightarrow \mathbb {R}$
and for every vector v in
$f:T^1 M\rightarrow \mathbb {R}$
and for every vector v in
![]() $\Sigma $
, there exists a sequence
$\Sigma $
, there exists a sequence
![]() $t_n\to +\infty $
such that the Birkhoff integral
$t_n\to +\infty $
such that the Birkhoff integral
![]() $\bar {M}_{e^{t_n}}(f)(v)$
tends to
$\bar {M}_{e^{t_n}}(f)(v)$
tends to
![]() $\lambda :=\int f \,\mathrm {d} \mu /\mu (T^1M)$
.
$\lambda :=\int f \,\mathrm {d} \mu /\mu (T^1M)$
.
There is a recurrent vector w in the unstable horocycle of v, since v is in
![]() $\Sigma $
. Let
$\Sigma $
. Let
![]() $t_n$
be a sequence tending to
$t_n$
be a sequence tending to
![]() $+\infty $
such that
$+\infty $
such that
![]() $g_{-t_n}(w)\to w$
. Then obviously
$g_{-t_n}(w)\to w$
. Then obviously
![]() $g_{-t_n}(v)$
also tends to w. We consider the compact set
$g_{-t_n}(v)$
also tends to w. We consider the compact set
![]() $K:=\{g_{-t_n}(v)\}_{n\ge 0}\cup \{w\}\subset \Sigma $
. By Proposition 3.5, the functions
$K:=\{g_{-t_n}(v)\}_{n\ge 0}\cup \{w\}\subset \Sigma $
. By Proposition 3.5, the functions
![]() $\bar {M}_1(f\circ g_{t})$
converge uniformly on K to the global average
$\bar {M}_1(f\circ g_{t})$
converge uniformly on K to the global average
![]() $\lambda $
of f. Therefore, using the time-scale relation, we have
$\lambda $
of f. Therefore, using the time-scale relation, we have
We can now prove that the restriction
![]() $\mu |_\Sigma $
of
$\mu |_\Sigma $
of
![]() $\mu $
to
$\mu $
to
![]() $\Sigma $
is the unique measure on
$\Sigma $
is the unique measure on
![]() $\Sigma $
invariant under
$\Sigma $
invariant under
![]() $h_s$
, up to a multiplicative constant. Suppose that
$h_s$
, up to a multiplicative constant. Suppose that
![]() $\nu $
is an ergodic
$\nu $
is an ergodic
![]() $h_s$
-invariant probability measure on
$h_s$
-invariant probability measure on
![]() $\Sigma $
. By the Birkhoff ergodic theorem, for every bounded and uniformly continuous function
$\Sigma $
. By the Birkhoff ergodic theorem, for every bounded and uniformly continuous function
![]() $f:\Sigma \rightarrow \mathbb {R}$
, for
$f:\Sigma \rightarrow \mathbb {R}$
, for
![]() $\nu $
-almost every v in
$\nu $
-almost every v in
![]() $\Sigma $
, we have
$\Sigma $
, we have
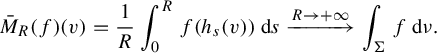 $$ \begin{align*} \bar{M}_R(f)(v)=\frac{1}{R}\int_0^R f(h_s(v))\,\mathrm{d} s\xrightarrow{R\to +\infty}\int_{\Sigma} f\,\mathrm{d} \nu. \end{align*} $$
$$ \begin{align*} \bar{M}_R(f)(v)=\frac{1}{R}\int_0^R f(h_s(v))\,\mathrm{d} s\xrightarrow{R\to +\infty}\int_{\Sigma} f\,\mathrm{d} \nu. \end{align*} $$
We take v one of the points of
![]() $\Sigma $
where
$\Sigma $
where
![]() $\bar {M}_R(f)$
converges to
$\bar {M}_R(f)$
converges to
![]() $\int f\, \mathrm {d} \nu $
. We can extend f to a bounded and uniformly continuous function
$\int f\, \mathrm {d} \nu $
. We can extend f to a bounded and uniformly continuous function
![]() $\hat {f}$
on
$\hat {f}$
on
![]() $T^1 M$
, because
$T^1 M$
, because
![]() $\Sigma $
is dense in
$\Sigma $
is dense in
![]() $T^1 M$
. As we have seen, there is a sequence
$T^1 M$
. As we have seen, there is a sequence
![]() $R_n=e^{t_n}$
where
$R_n=e^{t_n}$
where
![]() $\bar {M}_R(\hat {f})(v)=\bar {M}_R(f)(v)$
tends to
$\bar {M}_R(\hat {f})(v)=\bar {M}_R(f)(v)$
tends to
![]() $\lambda $
as well. So we obtain
$\lambda $
as well. So we obtain
 $$ \begin{align*} \int_{\Sigma} f\, \mathrm{d} \nu =\lambda =\frac{\int_{T^1M} f \, \mathrm{d} \mu}{\mu(T^1 M)} =\frac{\int_{\Sigma} f \,\mathrm{d} \mu}{\mu(\Sigma)}, \end{align*} $$
$$ \begin{align*} \int_{\Sigma} f\, \mathrm{d} \nu =\lambda =\frac{\int_{T^1M} f \, \mathrm{d} \mu}{\mu(T^1 M)} =\frac{\int_{\Sigma} f \,\mathrm{d} \mu}{\mu(\Sigma)}, \end{align*} $$
because
![]() $\Sigma $
has full
$\Sigma $
has full
![]() $\mu $
-measure. We have concluded that
$\mu $
-measure. We have concluded that
![]() $\nu $
is equal to the normalization of
$\nu $
is equal to the normalization of
![]() $\mu |_\Sigma $
.
$\mu |_\Sigma $
.
3.4 Alternative proof of the unique ergodicity
We would like to point out another way to prove Proposition 3.5, which does not require the equidistribution of horocycles (Theorem A). Instead, we use a version of the Arzelà–Ascoli theorem for the compact-open topology, the ergodic theorem and the fact that there exists a dense horocycle in
![]() $\Sigma $
. Actually, we can prove that all the horocycles of
$\Sigma $
. Actually, we can prove that all the horocycles of
![]() $\Sigma $
are dense.
$\Sigma $
are dense.
Lemma 3.7. Let M be a rank 1 non-positively curved complete connected Riemannian surface with the duality condition. Then every horocycle H contained in
![]() $\Sigma $
is dense in
$\Sigma $
is dense in
![]() $T^1M$
.
$T^1M$
.
Proof. This follows directly from two results of Eberlein. A non-positively curved complete connected manifold that satisfies the visibility axiom and the duality condition, like M, has a dense horocycle in
![]() $T^1M$
[Reference Eberlein7, Theorem 5.2]. Next we apply [Reference Eberlein7, Theorem 5.5] to M, which says that a horocycle
$T^1M$
[Reference Eberlein7, Theorem 5.2]. Next we apply [Reference Eberlein7, Theorem 5.5] to M, which says that a horocycle
![]() $H^u(v)$
in
$H^u(v)$
in
![]() $\mathcal {H}$
is dense in
$\mathcal {H}$
is dense in
![]() $T^1 M$
if and only if v is not almost minimizing. We say that v is almost minimizing if there exists a constant
$T^1 M$
if and only if v is not almost minimizing. We say that v is almost minimizing if there exists a constant
![]() $C>0$
such that, for all
$C>0$
such that, for all
![]() $t\ge 0$
, we have
$t\ge 0$
, we have
![]() $d(\pi (v),\pi (g_t(v)))\ge t -C$
. If a horocycle H is contained in
$d(\pi (v),\pi (g_t(v)))\ge t -C$
. If a horocycle H is contained in
![]() $\Sigma $
, then there is a recurrent vector in H and, in particular, this vector is not almost minimizing. Thus, the horocycle H is dense in
$\Sigma $
, then there is a recurrent vector in H and, in particular, this vector is not almost minimizing. Thus, the horocycle H is dense in
![]() $T^1 M$
$T^1 M$
We consider the space of continuous functions
![]() $C(\Sigma )$
on the set
$C(\Sigma )$
on the set
![]() $\Sigma $
equipped, this time, with the compact-open topology. Recall that, for functions on a metric space, the convergence in the compact-open topology is equivalent to the uniform convergence on compact subsets. The next fact will be used in the alternative proof of Proposition 3.5.
$\Sigma $
equipped, this time, with the compact-open topology. Recall that, for functions on a metric space, the convergence in the compact-open topology is equivalent to the uniform convergence on compact subsets. The next fact will be used in the alternative proof of Proposition 3.5.
Lemma 3.8. If a uniformly bounded sequence of functions
![]() $f_n$
in
$f_n$
in
![]() $C(\Sigma )$
converges in the compact-open topology to a function
$C(\Sigma )$
converges in the compact-open topology to a function
![]() $f\in C(\Sigma )$
, then the sequence also converges to f in the
$f\in C(\Sigma )$
, then the sequence also converges to f in the
![]() $L^2(\Sigma ,\mu |_\Sigma ) $
-norm.
$L^2(\Sigma ,\mu |_\Sigma ) $
-norm.
Proof. Recall that a Polish space is a separable completely metrizable topological space. The set of rank 1 recurrent vectors
![]() $Rec^1\subset \Sigma $
is a
$Rec^1\subset \Sigma $
is a
![]() $G_\delta $
subset of
$G_\delta $
subset of
![]() $T^1 M$
. Then
$T^1 M$
. Then
![]() $Rec^1$
is a Polish space, because
$Rec^1$
is a Polish space, because
![]() $G_\delta $
-subsets of Polish spaces are Polish spaces and
$G_\delta $
-subsets of Polish spaces are Polish spaces and
![]() $T^1 M$
is Polish.
$T^1 M$
is Polish.
Finite Borel measures on a Polish space are Radon. For
![]() $Rec^1 $
and the restriction of
$Rec^1 $
and the restriction of
![]() $\mu $
to
$\mu $
to
![]() $Rec^1$
, this means that, given any number
$Rec^1$
, this means that, given any number
![]() $\varepsilon>0$
, there is a compact set
$\varepsilon>0$
, there is a compact set
![]() $K\subset Rec^1$
such that
$K\subset Rec^1$
such that
![]() $\mu (Rec^1 \setminus K)<\varepsilon $
. In addition, the set
$\mu (Rec^1 \setminus K)<\varepsilon $
. In addition, the set
![]() $Rec^1 $
is of full measure in
$Rec^1 $
is of full measure in
![]() $T^1 M$
. We have
$T^1 M$
. We have
where C is a bound of f and the sequence
![]() $\{f_n\}$
. The last term tends to
$\{f_n\}$
. The last term tends to
![]() $0$
because of the uniform convergence of
$0$
because of the uniform convergence of
![]() $f_n$
to f on compact subsets.
$f_n$
to f on compact subsets.
Let f be a bounded and uniformly continuous function on
![]() $T^1M$
. Applying the Arzelà–Ascoli theorem for the compact-open topology [Reference Dugundji6, Theorem XII.6.4], since the family of functions
$T^1M$
. Applying the Arzelà–Ascoli theorem for the compact-open topology [Reference Dugundji6, Theorem XII.6.4], since the family of functions
![]() $\{\bar {M}_1(f\circ g_t)\}_{t>0}$
is equicontinuous and uniformly bounded, we obtain that it has a compact closure in
$\{\bar {M}_1(f\circ g_t)\}_{t>0}$
is equicontinuous and uniformly bounded, we obtain that it has a compact closure in
![]() $C(\Sigma )$
with the compact-open topology. To complete the proof of Proposition 3.5, we show that the only accumulation point of
$C(\Sigma )$
with the compact-open topology. To complete the proof of Proposition 3.5, we show that the only accumulation point of
![]() $\{\bar {M}_1(f\circ g_t)\}_{t>0}$
in the compact-open topology is the constant function
$\{\bar {M}_1(f\circ g_t)\}_{t>0}$
in the compact-open topology is the constant function
![]() $\int f\,\mathrm {d}\mu /\mu (T^1M)$
.
$\int f\,\mathrm {d}\mu /\mu (T^1M)$
.
Let
![]() $\varphi $
in
$\varphi $
in
![]() $C(\Sigma )$
be the limit of a sequence
$C(\Sigma )$
be the limit of a sequence
![]() $\bar {M}_1(f\circ g_{t_k})$
in the compact-open topology, where
$\bar {M}_1(f\circ g_{t_k})$
in the compact-open topology, where
![]() $t_k\to +\infty $
. By Lemma 3.8,
$t_k\to +\infty $
. By Lemma 3.8,
![]() $\varphi $
is the limit in
$\varphi $
is the limit in
![]() $L^2(\Sigma ,\mu |_\Sigma )$
of the same sequence. On the other hand, we apply the
$L^2(\Sigma ,\mu |_\Sigma )$
of the same sequence. On the other hand, we apply the
![]() $L^2$
ergodic theorem for the system
$L^2$
ergodic theorem for the system
![]() $(\Sigma ,h_s,\mu |_\Sigma )$
to the function
$(\Sigma ,h_s,\mu |_\Sigma )$
to the function
![]() $f\in L^2(\Sigma ,\mu |_\Sigma )$
. This says that
$f\in L^2(\Sigma ,\mu |_\Sigma )$
. This says that
![]() $\bar {M}_t(f)$
converges to an
$\bar {M}_t(f)$
converges to an
![]() $h_s$
-invariant function
$h_s$
-invariant function
![]() $\bar {f}$
in the
$\bar {f}$
in the
![]() $L^2$
norm, with the equality
$L^2$
norm, with the equality
![]() $\int \bar {f}\,\mathrm {d}\mu =\int f\,\mathrm {d}\mu $
. Thanks to
$\int \bar {f}\,\mathrm {d}\mu =\int f\,\mathrm {d}\mu $
. Thanks to
![]() $g_t$
invariance of
$g_t$
invariance of
![]() $\mu $
, we have the inequality
$\mu $
, we have the inequality
which implies the
![]() $L^2$
-convergence of
$L^2$
-convergence of
![]() $\bar {f}\circ g_{t_k}$
to
$\bar {f}\circ g_{t_k}$
to
![]() $\varphi $
, because both terms on the right-hand side tend to zero. The function
$\varphi $
, because both terms on the right-hand side tend to zero. The function
![]() $\bar {f}$
is
$\bar {f}$
is
![]() $h_s$
-invariant, so the
$h_s$
-invariant, so the
![]() $\bar {f}\circ g_{t_k}$
are also invariant because the geodesic and the horocyclic flow commute. Then their limit, the continuous function
$\bar {f}\circ g_{t_k}$
are also invariant because the geodesic and the horocyclic flow commute. Then their limit, the continuous function
![]() $\varphi $
of
$\varphi $
of
![]() $\Sigma $
, is also invariant under
$\Sigma $
, is also invariant under
![]() $h_s$
.
$h_s$
.
In brief, the function
![]() $\varphi $
is constant on the orbits of
$\varphi $
is constant on the orbits of
![]() $h_s$
, and these orbits are dense by Lemma 3.7. Since
$h_s$
, and these orbits are dense by Lemma 3.7. Since
![]() $\varphi $
is continuous, we conclude that it is constant on
$\varphi $
is continuous, we conclude that it is constant on
![]() $\Sigma $
. In fact, the value of the constant is
$\Sigma $
. In fact, the value of the constant is
![]() $\int f\,\mathrm {d}\mu /\mu (T^1M)$
, because we have
$\int f\,\mathrm {d}\mu /\mu (T^1M)$
, because we have
3.5 Final remark
Theorem B does not completely solve the problem of the horocyclic flow in non-positive curvature, since it does not say what happens to the flow outside the set
![]() $\Sigma $
. For instance, we wonder if a horocyclic flow defined everywhere on a compact non-positively curved surface is uniquely ergodic. We will study this question for the class of compact manifolds without flat strips in a forthcoming paper.
$\Sigma $
. For instance, we wonder if a horocyclic flow defined everywhere on a compact non-positively curved surface is uniquely ergodic. We will study this question for the class of compact manifolds without flat strips in a forthcoming paper.
Acknowledgement
The author wishes to thank his PhD advisor Yves Coudène for many helpful suggestions.
 This project has received funding from the European Union's Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant agreement no. 754362.
This project has received funding from the European Union's Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant agreement no. 754362.











