Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T13:26:02.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy ratio for infinite sequences with positive entropy

Published online by Cambridge University Press:  10 August 2018

CHRISTIAN MAUDUIT  and
CARLOS GUSTAVO MOREIRA
CHRISTIAN MAUDUIT
Affiliation:
Université d’Aix-Marseille et Institut Universitaire de France, Institut de Mathématiques de Marseille, UMR 7373 CNRS, 163, avenue de Luminy, 13288 Marseille Cedex 9, France
CARLOS GUSTAVO MOREIRA
Affiliation:
Instituto de Matemática Pura e Aplicada, Estrada Dona Castorina 110, 22460-320 Rio de Janeiro, RJ, Brazil
Get access Rights & Permissions [Opens in a new window]

Abstract

The complexity function of an infinite word 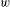$w$ on a finite alphabet $A$ is the sequence counting, for each non-negative $n$, the number of words of length $n$ on the alphabet $A$ that are factors of the infinite word 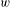$w$. For any given function 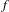$f$ with exponential growth, we introduced in [Complexity and fractal dimensions for infinite sequences with positive entropy. Commun. Contemp. Math. to appear] the notion of word entropy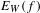$E_{W}(f)$ associated to 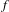$f$ and we described the combinatorial structure of sets of infinite words with a complexity function bounded by 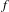$f$. The goal of this work is to give estimates on the word entropy 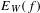$E_{W}(f)$ in terms of the limiting lower exponential growth rate of $f$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 3 , March 2020 , pp. 751 - 762
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Coven, E. M. and Hedlund, G. A.. Sequences with minimal block growth. Math. Systems Theory 7 (1973), 138–153.Google Scholar
Cassaigne, J. and Nicolas, F.. Factor complexity. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135) . Eds. Berth, V. and Rigo, M.. Cambridge University Press, Cambridge, 2010, pp. 163–247.Google Scholar
Fekete, M.. Uber der Verteilung der Wurzeln bei gewissen algebraischen Gleichungen mit ganzzahligen Koeffizienten. Math. Z. 17 (1923), 228–249.Google Scholar
Ferenczi, S.. Complexity of sequences and dynamical systems. Discrete Math. 206(1–3) (1999), 145–154.Google Scholar
Grillenberger, C.. Construction of strictly ergodic systems I. Given entropy. Z. Wahrscheinlichkeitstheorie verw. Geb. 25 (1973), 323–334.Google Scholar
Hedlund, G. A. and Morse, M.. Symbolics dynamics. Amer. J. Math. 60 (1938), 815–866.Google Scholar
Hedlund, G. A. and Morse, M.. Symbolics dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and Its Applications, 90) . Cambridge University Press, Cambridge, 2002.Google Scholar
Mauduit, C. and Moreira, C. G.. Complexity of infinite sequences with zero entropy. Acta Arith. 142 (2010), 331–346.Google Scholar
Mauduit, C. and Moreira, C. G.. Generalized Hausdorff dimensions of sets of real numbers with zero entropy expansion. Ergod. Th. & Dynam. Sys. 32 (2012), 1073–1089.Google Scholar
Mauduit, C. and Moreira, C. G.. Complexity and fractal dimensions for infinite sequences with positive entropy. Commun. Contemp. Math. to appear.Google Scholar
Pytheas Fogg, N.. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794) . Eds. Berthé, V., Ferenczi, S., Mauduit, C. and Siegel, A.. Springer, Berlin, 2002.Google Scholar