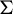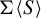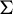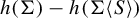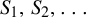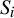1 Introduction
Let n be a positive integer and let T be an irreducible
![]() $n\times n$
matrix with entries in
$n\times n$
matrix with entries in
![]() $\{0,1\}$
. This determines a subshift of finite type
$\{0,1\}$
. This determines a subshift of finite type
![]() $\Sigma $
defined as the collection of all bi-infinite strings
$\Sigma $
defined as the collection of all bi-infinite strings
![]() $(x_i)$
on an alphabet of n symbols indexing the rows and columns of T that are admissible in the sense that the
$(x_i)$
on an alphabet of n symbols indexing the rows and columns of T that are admissible in the sense that the
![]() $(x_{i+1},x_i)$
entry in T is equal to
$(x_{i+1},x_i)$
entry in T is equal to
![]() $1$
for all
$1$
for all
![]() $i\in \mathbb {Z}$
. Recall that the largest eigenvalue,
$i\in \mathbb {Z}$
. Recall that the largest eigenvalue,
![]() $\unicode{x3bb} $
, of T is related to the shift entropy of
$\unicode{x3bb} $
, of T is related to the shift entropy of
![]() $\Sigma $
by
$\Sigma $
by
![]() $\unicode{x3bb} = e^{h(\Sigma )}$
, and we assume throughout that
$\unicode{x3bb} = e^{h(\Sigma )}$
, and we assume throughout that
![]() $\unicode{x3bb}>1$
. Let S denote a finite set of finite admissible non-empty words none of which contains another, and let
$\unicode{x3bb}>1$
. Let S denote a finite set of finite admissible non-empty words none of which contains another, and let
![]() $\Sigma \langle S\rangle $
denote the subshift of
$\Sigma \langle S\rangle $
denote the subshift of
![]() $\Sigma $
consisting of those elements of
$\Sigma $
consisting of those elements of
![]() $\Sigma $
in which none of the words in S appear.
$\Sigma $
in which none of the words in S appear.
We are interested in the entropy of the perturbed subshift
![]() $\Sigma \langle S\rangle $
, and in particular seek to bound the entropy difference
$\Sigma \langle S\rangle $
, and in particular seek to bound the entropy difference
![]() $h(\Sigma ) - h(\Sigma \langle S\rangle )$
. In [Reference Lind4], Lind addressed this problem in the case where S consists of a single word, and proved that the entropy of
$h(\Sigma ) - h(\Sigma \langle S\rangle )$
. In [Reference Lind4], Lind addressed this problem in the case where S consists of a single word, and proved that the entropy of
![]() $\Sigma \langle S \rangle $
approaches that of
$\Sigma \langle S \rangle $
approaches that of
![]() $\Sigma $
as the length
$\Sigma $
as the length
![]() $\ell $
of the word tends to infinity. He showed, moreover, that the difference in entropy is of exact order
$\ell $
of the word tends to infinity. He showed, moreover, that the difference in entropy is of exact order
![]() $O(\unicode{x3bb} ^{-\ell })$
in the sense that it is bounded above and below by a constant multiple of
$O(\unicode{x3bb} ^{-\ell })$
in the sense that it is bounded above and below by a constant multiple of
![]() $\unicode{x3bb} ^{-\ell }$
. Lind’s entropy bounds stem from a lower bound on the correlation polynomial associated to the word in S. Such polynomials were studied by Guibas and Odlyzko in a series of papers [Reference Guibas and Odlyzko1–Reference Guibas and Odlyzko3], where they attribute the original definition to J. H. Conway.
$\unicode{x3bb} ^{-\ell }$
. Lind’s entropy bounds stem from a lower bound on the correlation polynomial associated to the word in S. Such polynomials were studied by Guibas and Odlyzko in a series of papers [Reference Guibas and Odlyzko1–Reference Guibas and Odlyzko3], where they attribute the original definition to J. H. Conway.
In [Reference Ramsey8], the author adapted Lind’s method to the case where S has more than one word. Here, one can define an
![]() $|S|\times |S|$
matrix of correlation polynomials analogous to the correlation polynomial for a single word, and an entropy bound comes down to a certain lower bound on the determinant of this matrix. Analyzing the size of this determinant gets complicated as S grows, and we were only able to effectively bound the entropy and show that it approximates that of
$|S|\times |S|$
matrix of correlation polynomials analogous to the correlation polynomial for a single word, and an entropy bound comes down to a certain lower bound on the determinant of this matrix. Analyzing the size of this determinant gets complicated as S grows, and we were only able to effectively bound the entropy and show that it approximates that of
![]() $\Sigma $
in the case where S consists of two words of length tending to infinity. The entropy perturbation in this case is shown to be of order at most
$\Sigma $
in the case where S consists of two words of length tending to infinity. The entropy perturbation in this case is shown to be of order at most
![]() $O(\unicode{x3bb} ^{-\ell })$
where
$O(\unicode{x3bb} ^{-\ell })$
where
![]() $\ell $
is the length of the shorter word. Here again this must be the exact order, as can be seen by throwing out the longer word and appealing to Lind’s lower bound for the remaining word of length
$\ell $
is the length of the shorter word. Here again this must be the exact order, as can be seen by throwing out the longer word and appealing to Lind’s lower bound for the remaining word of length
![]() $\ell $
. The correlation polynomial determinant seems to be a very natural quantity in this setting and deserving of further study with an eye towards adapting Lind’s method more broadly, as it seems to give very sharp bounds. We note also that Pavlov in [Reference Pavlov7] has proven a result analogous to Lind’s one-word result in the setting of multidimensional shifts.
$\ell $
. The correlation polynomial determinant seems to be a very natural quantity in this setting and deserving of further study with an eye towards adapting Lind’s method more broadly, as it seems to give very sharp bounds. We note also that Pavlov in [Reference Pavlov7] has proven a result analogous to Lind’s one-word result in the setting of multidimensional shifts.
In [Reference Miller5], Miller considered the following related problem: given a finite set S of finite non-empty words in a finite alphabet, determine whether there exists a infinite word in the alphabet that avoids S. Note that the ambient shift here is constrained to the full shift, while the set S is quite flexible. Miller defines
and establishes a simple numerical criterion involving
![]() $p(t)$
that ensures that his perturbation is non-empty. In this paper, we adapt Miller’s method to a general subshift of finite type (SFT) and refine it to get lower bounds on the entropy of
$p(t)$
that ensures that his perturbation is non-empty. In this paper, we adapt Miller’s method to a general subshift of finite type (SFT) and refine it to get lower bounds on the entropy of
![]() $\Sigma \langle S\rangle $
, and thus upper bounds on the entropy perturbation. Our main result is as follows.
$\Sigma \langle S\rangle $
, and thus upper bounds on the entropy perturbation. Our main result is as follows.
Theorem 1. There exists a constant
![]() $C>0$
depending only on
$C>0$
depending only on
![]() $\Sigma $
such that if k is a positive integer, every element of S has length at least k, and there exists
$\Sigma $
such that if k is a positive integer, every element of S has length at least k, and there exists
![]() $t\in (1,\unicode{x3bb} ^k)$
with
$t\in (1,\unicode{x3bb} ^k)$
with
then
This theorem is shown to have consequences for the ‘growing words’ problems above. A perturbation bound of
![]() $O(\unicode{x3bb} ^{-\ell })$
seems beyond the method, but we can establish
$O(\unicode{x3bb} ^{-\ell })$
seems beyond the method, but we can establish
![]() $O(\ell ^{-3/4}\unicode{x3bb} ^{-\ell /8})$
when S consists of any fixed number of words of minimal length
$O(\ell ^{-3/4}\unicode{x3bb} ^{-\ell /8})$
when S consists of any fixed number of words of minimal length
![]() $\ell \to \infty $
. The method can also be applied to a growing set of words of increasing length with sufficient control over the growth, as illustrated by the following result. Suppose that
$\ell \to \infty $
. The method can also be applied to a growing set of words of increasing length with sufficient control over the growth, as illustrated by the following result. Suppose that
![]() $S_1, S_2, \ldots $
is a sequence of sets as above, let
$S_1, S_2, \ldots $
is a sequence of sets as above, let
![]() $\ell _i$
denote the minimal length in
$\ell _i$
denote the minimal length in
![]() $S_i$
, and suppose
$S_i$
, and suppose
![]() $\ell _i\to \infty $
.
$\ell _i\to \infty $
.
Theorem 2. Suppose there exists
![]() $\kappa {<}\,\unicode{x3bb} $
such that
$\kappa {<}\,\unicode{x3bb} $
such that
![]() $|S_i| = O(\kappa ^{\ell _i})$
as
$|S_i| = O(\kappa ^{\ell _i})$
as
![]() $i\to \infty $
. Then
$i\to \infty $
. Then
2 Parry measure and the weight function
 $w(\sigma )$
$w(\sigma )$
Let u and v denote left and right
![]() $\unicode{x3bb} $
-eigenvectors for T normalized so that
$\unicode{x3bb} $
-eigenvectors for T normalized so that
![]() $u^t v=1$
. The entries of these vectors measure the prominence of the corresponding symbols as a sink and source in
$u^t v=1$
. The entries of these vectors measure the prominence of the corresponding symbols as a sink and source in
![]() $\Sigma $
, respectively. More precisely,
$\Sigma $
, respectively. More precisely,
![]() $u_i/\sum u_i$
is the fraction of paths on the directed graph associated to T that terminate at i, while
$u_i/\sum u_i$
is the fraction of paths on the directed graph associated to T that terminate at i, while
![]() $v_i/\sum v_i$
is the fraction of paths that begin at i. In [Reference Parry6], Parry defined a shift-invariant measure of maximal entropy
$v_i/\sum v_i$
is the fraction of paths that begin at i. In [Reference Parry6], Parry defined a shift-invariant measure of maximal entropy
![]() $\mu $
on
$\mu $
on
![]() $\Sigma $
that can be characterized on non-empty cylinder sets by
$\Sigma $
that can be characterized on non-empty cylinder sets by
Note that the notation
![]() $[\sigma ]$
only defines a cylinder set up to shifts. Where it is important to have an actual set to work with (e.g., in defining
$[\sigma ]$
only defines a cylinder set up to shifts. Where it is important to have an actual set to work with (e.g., in defining
![]() $f_{\sigma }$
below) we take
$f_{\sigma }$
below) we take
![]() $\sigma $
to begin at coordinate
$\sigma $
to begin at coordinate
![]() $0$
in forming
$0$
in forming
![]() $[\sigma ]$
. If
$[\sigma ]$
. If
![]() $\sigma $
fails to be admissible, then
$\sigma $
fails to be admissible, then
![]() $[\sigma ]$
is taken to be empty.
$[\sigma ]$
is taken to be empty.
Let
![]() $N(\sigma ,k)$
denote the number of words
$N(\sigma ,k)$
denote the number of words
![]() $\eta $
of length k such that
$\eta $
of length k such that
![]() $\sigma \eta $
is admissible. Since T is irreducible, it follows from Perron–Frobenius theory that there exist positive constants
$\sigma \eta $
is admissible. Since T is irreducible, it follows from Perron–Frobenius theory that there exist positive constants
![]() $A, B$
such that
$A, B$
such that
for all words
![]() $\sigma $
and all
$\sigma $
and all
![]() $k\geq 1$
. Let D denote the maximum ratio among the
$k\geq 1$
. Let D denote the maximum ratio among the
![]() $v_i$
.
$v_i$
.
Lemma 1. We have
for all words
![]() $\sigma , \tau $
.
$\sigma , \tau $
.
Proof. We may assume that
![]() $\sigma \tau $
is admissible, for otherwise the result is trivial. The explicit description of
$\sigma \tau $
is admissible, for otherwise the result is trivial. The explicit description of
![]() $\mu $
on cylinder sets implies that D is an upper bound for the ratio among the
$\mu $
on cylinder sets implies that D is an upper bound for the ratio among the
![]() $\mu ([\sigma \eta ])$
as
$\mu ([\sigma \eta ])$
as
![]() $\eta $
varies among the words of a given positive length for which
$\eta $
varies among the words of a given positive length for which
![]() $\sigma \eta $
is admissible. Thus,
$\sigma \eta $
is admissible. Thus,
 $$ \begin{align*} \unicode{x3bb}^{|\tau|}\mu([\sigma\tau]) \leq A^{-1}N(\sigma,|\tau|)\mu([\sigma\tau]) &= A^{-1}\sum_{\eta}\mu([\sigma\tau]) \\ & \leq A^{-1}\sum_{\eta} D\mu([\sigma\eta]) \\ &= DA^{-1}\mu([\sigma]) \end{align*} $$
$$ \begin{align*} \unicode{x3bb}^{|\tau|}\mu([\sigma\tau]) \leq A^{-1}N(\sigma,|\tau|)\mu([\sigma\tau]) &= A^{-1}\sum_{\eta}\mu([\sigma\tau]) \\ & \leq A^{-1}\sum_{\eta} D\mu([\sigma\eta]) \\ &= DA^{-1}\mu([\sigma]) \end{align*} $$
where the sums are taken over those
![]() $\eta $
with
$\eta $
with
![]() $|\eta |=|\tau |$
and
$|\eta |=|\tau |$
and
![]() $\sigma \eta $
admissible.
$\sigma \eta $
admissible.
Let
![]() $\sigma $
be an admissible word and let
$\sigma $
be an admissible word and let
![]() $[\sigma ]$
denote the associated cylinder set. Define a polynomial-valued function
$[\sigma ]$
denote the associated cylinder set. Define a polynomial-valued function
![]() $f_{\sigma }$
on
$f_{\sigma }$
on
![]() $[\sigma ]$
by
$[\sigma ]$
by
 $$ \begin{align*} f_{\sigma}(\alpha) = \sum_{\tau\in S}\sum_j t^j \end{align*} $$
$$ \begin{align*} f_{\sigma}(\alpha) = \sum_{\tau\in S}\sum_j t^j \end{align*} $$
where the inner sum is over
![]() $j\geq 0$
such that
$j\geq 0$
such that
![]() $\tau $
occurs in
$\tau $
occurs in
![]() $\alpha $
beginning within
$\alpha $
beginning within
![]() $\sigma $
and ending j symbols beyond the end of
$\sigma $
and ending j symbols beyond the end of
![]() $\sigma $
:
$\sigma $
:

Observe that the function
![]() $f_{\sigma }$
is locally constant on
$f_{\sigma }$
is locally constant on
![]() $[\sigma ]$
. We define a weight function on admissible words by
$[\sigma ]$
. We define a weight function on admissible words by
 $$ \begin{align*}w(\sigma) = \frac{1}{\mu([\sigma])}\int_{[\sigma]}f_{\sigma} \,d\mu.\end{align*} $$
$$ \begin{align*}w(\sigma) = \frac{1}{\mu([\sigma])}\int_{[\sigma]}f_{\sigma} \,d\mu.\end{align*} $$
Note that the empty word
![]() $\sigma _0$
has cylinder set
$\sigma _0$
has cylinder set
![]() $[\sigma _0]=\Sigma $
and weight
$[\sigma _0]=\Sigma $
and weight
![]() $0$
. Since no element of S contains another, for each
$0$
. Since no element of S contains another, for each
![]() $j\geq 0$
there is at most one element of S that ends j symbols after then of
$j\geq 0$
there is at most one element of S that ends j symbols after then of
![]() $\sigma $
, so we may write
$\sigma $
, so we may write
 $$ \begin{align} w(\sigma) = \sum_{j\geq 0} \frac{\mu(S_{\sigma,j})}{\mu([\sigma])} t^j \end{align} $$
$$ \begin{align} w(\sigma) = \sum_{j\geq 0} \frac{\mu(S_{\sigma,j})}{\mu([\sigma])} t^j \end{align} $$
where
![]() $S_{\sigma ,j}$
denotes the subset of
$S_{\sigma ,j}$
denotes the subset of
![]() $[\sigma ]$
containing an element
$[\sigma ]$
containing an element
![]() $\tau \in S$
that begins in
$\tau \in S$
that begins in
![]() $\sigma $
and ends j symbols after the end of
$\sigma $
and ends j symbols after the end of
![]() $\sigma $
. Observe that if
$\sigma $
. Observe that if
![]() $\sigma $
ends in an element of S, then we have
$\sigma $
ends in an element of S, then we have
![]() $S_{\sigma ,0}=[\sigma ]$
and hence
$S_{\sigma ,0}=[\sigma ]$
and hence
![]() $w(\sigma )\geq 1$
. In general, the weight
$w(\sigma )\geq 1$
. In general, the weight
![]() $w(\sigma )$
is a measure of how close
$w(\sigma )$
is a measure of how close
![]() $\sigma $
is to ending in an element of S. The strategy here is study how w changes as you extend
$\sigma $
is to ending in an element of S. The strategy here is study how w changes as you extend
![]() $\sigma $
to the right by computing its weighted averages, and then use the results to bound from below the number of S-free extensions of
$\sigma $
to the right by computing its weighted averages, and then use the results to bound from below the number of S-free extensions of
![]() $\sigma $
and ultimately the entropy of
$\sigma $
and ultimately the entropy of
![]() $\Sigma \langle S\rangle $
.
$\Sigma \langle S\rangle $
.
Define
 $$ \begin{align*}p_{\sigma} = \sum_{\tau\in S}\frac{\mu([\sigma\tau])}{\mu([\sigma])}t^{|\tau|}.\end{align*} $$
$$ \begin{align*}p_{\sigma} = \sum_{\tau\in S}\frac{\mu([\sigma\tau])}{\mu([\sigma])}t^{|\tau|}.\end{align*} $$
Lemma 1 furnishes the upper bound
which is independent of
![]() $\sigma $
.
$\sigma $
.
Lemma 2. If
![]() $\sigma $
does not end in an element of S, then
$\sigma $
does not end in an element of S, then
 $$ \begin{align*}\frac{1}{\mu([\sigma])}\sum_i \mu([\sigma i])w(\sigma i) = \frac{w(\sigma)+p_{\sigma}}{t}.\end{align*} $$
$$ \begin{align*}\frac{1}{\mu([\sigma])}\sum_i \mu([\sigma i])w(\sigma i) = \frac{w(\sigma)+p_{\sigma}}{t}.\end{align*} $$
Proof. Using (2),
 $$ \begin{align} \frac{1}{\mu([\sigma])}\sum_i\mu([\sigma i])w(\sigma i) = \frac{1}{\mu([\sigma])}\sum_i\sum_j\mu(S_{\sigma i,j})t^j. \end{align} $$
$$ \begin{align} \frac{1}{\mu([\sigma])}\sum_i\mu([\sigma i])w(\sigma i) = \frac{1}{\mu([\sigma])}\sum_i\sum_j\mu(S_{\sigma i,j})t^j. \end{align} $$
An element of
![]() $S_{\sigma i,j}$
has a unique
$S_{\sigma i,j}$
has a unique
![]() $\tau \in S$
ending j symbols after
$\tau \in S$
ending j symbols after
![]() $\sigma i$
and beginning within
$\sigma i$
and beginning within
![]() $\sigma i$
. This
$\sigma i$
. This
![]() $\tau $
can begin either within
$\tau $
can begin either within
![]() $\sigma $
or at the final symbol i, and accordingly we may decompose
$\sigma $
or at the final symbol i, and accordingly we may decompose
![]() $S_{\sigma i,j} = A_{\sigma i,j}\sqcup B_{\sigma i,j}$
. Explicitly, the set
$S_{\sigma i,j} = A_{\sigma i,j}\sqcup B_{\sigma i,j}$
. Explicitly, the set
![]() $A_{\sigma i,j}$
consists of elements of
$A_{\sigma i,j}$
consists of elements of
![]() $[\sigma i]$
that contains a word in S beginning within
$[\sigma i]$
that contains a word in S beginning within
![]() $\sigma $
and ending j symbols after
$\sigma $
and ending j symbols after
![]() $\sigma i$
. The set
$\sigma i$
. The set
![]() $B_{\sigma i, j}$
consists of elements of
$B_{\sigma i, j}$
consists of elements of
![]() $[\sigma i]$
in which
$[\sigma i]$
in which
![]() $\sigma $
is immediately followed by an element of S of length
$\sigma $
is immediately followed by an element of S of length
![]() $j+1$
. Observe that
$j+1$
. Observe that
and
 $$ \begin{align*} \bigsqcup_iB_{\sigma i,j} = \bigsqcup_{\substack{\tau\in S\\|\tau|=j+1}}[\sigma\tau] \end{align*} $$
$$ \begin{align*} \bigsqcup_iB_{\sigma i,j} = \bigsqcup_{\substack{\tau\in S\\|\tau|=j+1}}[\sigma\tau] \end{align*} $$
are both clear from the definitions. Thus, (4) is equal to
 $$ \begin{align*} \sum_j\bigg(\frac{\mu(S_{\sigma,j+1})}{\mu([\sigma])}+\sum_{\substack{\tau\in S\\|\tau|=j+1}}\frac{\mu([\sigma\tau])}{\mu([\sigma])}\bigg)t^j = \frac{w(\sigma)+p_{\sigma}}{t}. \end{align*} $$
$$ \begin{align*} \sum_j\bigg(\frac{\mu(S_{\sigma,j+1})}{\mu([\sigma])}+\sum_{\substack{\tau\in S\\|\tau|=j+1}}\frac{\mu([\sigma\tau])}{\mu([\sigma])}\bigg)t^j = \frac{w(\sigma)+p_{\sigma}}{t}. \end{align*} $$
Note that the last equality relies on the fact that
![]() $\sigma $
does not end in an element of S, so the apparently missing
$\sigma $
does not end in an element of S, so the apparently missing
![]() $\mu (S_{\sigma ,0})$
in the sum on the left vanishes.
$\mu (S_{\sigma ,0})$
in the sum on the left vanishes.
3 Bounding entropy
Fix some
![]() $t>1$
for the moment and let
$t>1$
for the moment and let
![]() $\sigma $
be an S-free word with
$\sigma $
be an S-free word with
![]() $w(\sigma )<1$
. We say that a word
$w(\sigma )<1$
. We say that a word
![]() $\eta $
is good if
$\eta $
is good if
![]() $\sigma \eta $
is admissible and every intermediate word between
$\sigma \eta $
is admissible and every intermediate word between
![]() $\sigma $
and
$\sigma $
and
![]() $\sigma \eta $
(inclusive) has weight
$\sigma \eta $
(inclusive) has weight
![]() $w<1$
. In particular,
$w<1$
. In particular,
![]() $\sigma \eta $
is S-free if
$\sigma \eta $
is S-free if
![]() $\eta $
is good, since words ending in an element of S have weight greater than or equal to
$\eta $
is good, since words ending in an element of S have weight greater than or equal to
![]() $1$
. For a positive integer m, set
$1$
. For a positive integer m, set
 $$ \begin{align*} G(\sigma,m) = \bigsqcup_{\substack{\eta\ \mathrm{good}\\ |\eta|=m}} [\sigma\eta]. \end{align*} $$
$$ \begin{align*} G(\sigma,m) = \bigsqcup_{\substack{\eta\ \mathrm{good}\\ |\eta|=m}} [\sigma\eta]. \end{align*} $$
Lemma 3. Suppose
![]() $({1+p_{\rho }})/{t} < r<1$
for all words
$({1+p_{\rho }})/{t} < r<1$
for all words
![]() $\rho $
, and let
$\rho $
, and let
![]() $\sigma $
be S-free with
$\sigma $
be S-free with
![]() ${w(\sigma )<1}$
. We have
${w(\sigma )<1}$
. We have
for all
![]() $m\geq 1$
.
$m\geq 1$
.
Proof. Since extensions
![]() $\sigma i$
that end in an element of S have
$\sigma i$
that end in an element of S have
![]() $w(\sigma i)\geq 1$
, we have
$w(\sigma i)\geq 1$
, we have
Thus,
 $$ \begin{align*} \frac{\mu(G(\sigma,1))}{\mu([\sigma])}\geq 1-\frac{1}{\mu([\sigma])}\sum_i\mu([\sigma i])w(\sigma i)=1 - \bigg(\frac{w(\sigma)+p_{\sigma}}{t}\bigg) \geq 1-r, \end{align*} $$
$$ \begin{align*} \frac{\mu(G(\sigma,1))}{\mu([\sigma])}\geq 1-\frac{1}{\mu([\sigma])}\sum_i\mu([\sigma i])w(\sigma i)=1 - \bigg(\frac{w(\sigma)+p_{\sigma}}{t}\bigg) \geq 1-r, \end{align*} $$
which establishes the case
![]() $m=1$
.
$m=1$
.
Suppose the statement holds for some
![]() $m\geq 1$
and all
$m\geq 1$
and all
![]() $\sigma $
. Observe that
$\sigma $
. Observe that
 $$ \begin{align*} G(\sigma,m+1) = \bigsqcup_{\substack{\eta\ \mathrm{good}\\ |\eta|=m}} G(\sigma\eta,1). \end{align*} $$
$$ \begin{align*} G(\sigma,m+1) = \bigsqcup_{\substack{\eta\ \mathrm{good}\\ |\eta|=m}} G(\sigma\eta,1). \end{align*} $$
For good
![]() $\eta $
, the word
$\eta $
, the word
![]() $\sigma \eta $
is S-free and has
$\sigma \eta $
is S-free and has
![]() $w(\sigma \eta )<1$
, so the base case and induction hypothesis give
$w(\sigma \eta )<1$
, so the base case and induction hypothesis give
 $$ \begin{align*} \mu(G(\sigma,m+1)) &= \sum_{\substack{\eta\ \mathrm{good}\\|\eta|=m}} \mu(G(\sigma\eta,1)) \geq \sum_{\substack{\eta\ \mathrm{good}\\|\eta|=m}} (1-r)\mu([\sigma\eta])\\ &= (1-r)G(\sigma,m)\geq (1-r)^{m+1}\mu([\sigma]), \end{align*} $$
$$ \begin{align*} \mu(G(\sigma,m+1)) &= \sum_{\substack{\eta\ \mathrm{good}\\|\eta|=m}} \mu(G(\sigma\eta,1)) \geq \sum_{\substack{\eta\ \mathrm{good}\\|\eta|=m}} (1-r)\mu([\sigma\eta])\\ &= (1-r)G(\sigma,m)\geq (1-r)^{m+1}\mu([\sigma]), \end{align*} $$
which establishes case
![]() $m+1$
.
$m+1$
.
Proposition 1. Suppose
![]() $r = ({1+DA^{-1}p(t/\unicode{x3bb} )})/{t} < 1$
. We have
$r = ({1+DA^{-1}p(t/\unicode{x3bb} )})/{t} < 1$
. We have
![]() $h(\Sigma ) - h(\Sigma \langle S\rangle ) \leq {-}\!\log (1-r)$
.
$h(\Sigma ) - h(\Sigma \langle S\rangle ) \leq {-}\!\log (1-r)$
.
Proof. Using (3), we may apply Lemma 3 to the empty word
![]() $\sigma _0$
and conclude
$\sigma _0$
and conclude
![]() ${\mu (G(\sigma _0,m))}/{\mu ([\sigma _0])}\geq (1-r)^m$
. The set
${\mu (G(\sigma _0,m))}/{\mu ([\sigma _0])}\geq (1-r)^m$
. The set
![]() $[\sigma _0]$
is simply
$[\sigma _0]$
is simply
![]() $\Sigma $
, but we retain
$\Sigma $
, but we retain
![]() $\sigma _0$
below for clarity. If g denotes the number of good
$\sigma _0$
below for clarity. If g denotes the number of good
![]() $\eta $
of length m, then by Lemma 1 we have
$\eta $
of length m, then by Lemma 1 we have
 $$ \begin{align*} \frac{G(\sigma_0,m)}{\mu([\sigma_0])}=\sum_{\eta}\frac{\mu([\sigma_0\eta])}{\mu([\sigma_0])}\leq gDA^{-1}\unicode{x3bb}^{-m} \end{align*} $$
$$ \begin{align*} \frac{G(\sigma_0,m)}{\mu([\sigma_0])}=\sum_{\eta}\frac{\mu([\sigma_0\eta])}{\mu([\sigma_0])}\leq gDA^{-1}\unicode{x3bb}^{-m} \end{align*} $$
where the sum is over such
![]() $\eta $
. Thus, we have produced for every
$\eta $
. Thus, we have produced for every
![]() $m\geq 1$
at least
$m\geq 1$
at least
words of length m that are S-free, which implies that the entropy of
![]() $\Sigma \langle S\rangle $
is at least
$\Sigma \langle S\rangle $
is at least
Since
![]() $\Sigma $
has entropy
$\Sigma $
has entropy
![]() $\log (\unicode{x3bb} )$
, this is the desired result.
$\log (\unicode{x3bb} )$
, this is the desired result.
4 Blocking
The condition
![]() $r = ({1+DA^{-1}p(t/\unicode{x3bb} )})/{t} < 1$
in Proposition 1 implies
$r = ({1+DA^{-1}p(t/\unicode{x3bb} )})/{t} < 1$
in Proposition 1 implies
![]() $t>1$
but also effectively limits t from above to roughly
$t>1$
but also effectively limits t from above to roughly
![]() $\unicode{x3bb} $
. This in turn bounds r from below, limiting the direct utility of Proposition 1. The solution is to work with blocks of elements in
$\unicode{x3bb} $
. This in turn bounds r from below, limiting the direct utility of Proposition 1. The solution is to work with blocks of elements in
![]() $\Sigma $
. For each
$\Sigma $
. For each
![]() $k\geq 1$
let
$k\geq 1$
let
![]() $\Sigma _k$
denote the SFT on the alphabet of admissible words of length k in
$\Sigma _k$
denote the SFT on the alphabet of admissible words of length k in
![]() $\Sigma $
, where the transition
$\Sigma $
, where the transition
![]() $[x_1\cdots x_k][y_1\cdots y_k]$
is admissible in
$[x_1\cdots x_k][y_1\cdots y_k]$
is admissible in
![]() $\Sigma _k$
if and only if
$\Sigma _k$
if and only if
![]() $x_ky_1$
is admissible in
$x_ky_1$
is admissible in
![]() $\Sigma $
. Concatenating blocks furnishes a natural bijection
$\Sigma $
. Concatenating blocks furnishes a natural bijection
![]() $\Sigma _k\longrightarrow \Sigma $
that intertwines the shift map on
$\Sigma _k\longrightarrow \Sigma $
that intertwines the shift map on
![]() $\Sigma _k$
with the kth power of the shift map on
$\Sigma _k$
with the kth power of the shift map on
![]() $\Sigma $
. Accordingly, we have
$\Sigma $
. Accordingly, we have
![]() $h(\Sigma _k) = kh(\Sigma )$
.
$h(\Sigma _k) = kh(\Sigma )$
.
To use the technique of the previous section, we must translate the collection S of forbidden words into an equivalent collection
![]() $S_k$
of words in
$S_k$
of words in
![]() $\Sigma _k$
, that is, one that cuts out the same subshift under the above bijection. In the process, we will also bound the associated polynomial
$\Sigma _k$
, that is, one that cuts out the same subshift under the above bijection. In the process, we will also bound the associated polynomial
 $$ \begin{align*} p_k(t) = \sum_{\zeta\in S_k}t^{|\zeta|}. \end{align*} $$
$$ \begin{align*} p_k(t) = \sum_{\zeta\in S_k}t^{|\zeta|}. \end{align*} $$
Let
![]() $\tau \in S$
have length
$\tau \in S$
have length
![]() $\ell $
, suppose that
$\ell $
, suppose that
![]() $k\leq \ell $
, and write
$k\leq \ell $
, and write
![]() $\ell = kq+s$
with
$\ell = kq+s$
with
![]() $0\leq s< k$
according to the division algorithm. To determine a collection of words in
$0\leq s< k$
according to the division algorithm. To determine a collection of words in
![]() $\Sigma _k$
that forbids
$\Sigma _k$
that forbids
![]() $\tau $
in
$\tau $
in
![]() $\Sigma $
, we must consider each of the k ways of tiling over
$\Sigma $
, we must consider each of the k ways of tiling over
![]() $\tau $
by blocks of length k, according to the k possible positions of the beginning of
$\tau $
by blocks of length k, according to the k possible positions of the beginning of
![]() $\tau $
in the first block. Of these k positions,
$\tau $
in the first block. Of these k positions,
![]() $s+1$
require
$s+1$
require
![]() $b=\lceil \ell /k\rceil $
blocks to tile over
$b=\lceil \ell /k\rceil $
blocks to tile over
![]() $\tau $
. Here,
$\tau $
. Here,
![]() $kb-\ell $
coordinates remain unspecified by
$kb-\ell $
coordinates remain unspecified by
![]() $\tau $
, which means that we have at most
$\tau $
, which means that we have at most
![]() $B\unicode{x3bb} ^{kb-\ell }$
words to consider at this position by (1). The remaining
$B\unicode{x3bb} ^{kb-\ell }$
words to consider at this position by (1). The remaining
![]() $k-s-1$
positions require
$k-s-1$
positions require
![]() $b+1$
blocks to tile over
$b+1$
blocks to tile over
![]() $\tau $
and leave
$\tau $
and leave
![]() $k(b+1)-\ell $
free coordinates.
$k(b+1)-\ell $
free coordinates.

The total contribution to
![]() $p_k(t)$
of the words associated to
$p_k(t)$
of the words associated to
![]() $\tau $
is thus at most
$\tau $
is thus at most
Assuming that
![]() $1\leq t\leq \unicode{x3bb} ^k$
, the contribution of
$1\leq t\leq \unicode{x3bb} ^k$
, the contribution of
![]() $\tau $
to
$\tau $
to
![]() $p_k(t/\unicode{x3bb} ^k)$
is then at most
$p_k(t/\unicode{x3bb} ^k)$
is then at most
 $$ \begin{align*} (s+1)B\unicode{x3bb}^{-\ell}t^b+(k-s-1)B\unicode{x3bb}^{-\ell}t^{b+1} &\leq (s+1)B\unicode{x3bb}^{k-\ell}t^{b-1}+(k-s-1)B\unicode{x3bb}^{2k-\ell}t^{b-1} \\ &\leq kB\unicode{x3bb}^{2k-\ell}t^{{\ell}/{k}}. \end{align*} $$
$$ \begin{align*} (s+1)B\unicode{x3bb}^{-\ell}t^b+(k-s-1)B\unicode{x3bb}^{-\ell}t^{b+1} &\leq (s+1)B\unicode{x3bb}^{k-\ell}t^{b-1}+(k-s-1)B\unicode{x3bb}^{2k-\ell}t^{b-1} \\ &\leq kB\unicode{x3bb}^{2k-\ell}t^{{\ell}/{k}}. \end{align*} $$
Summing over
![]() $\tau \in S$
, we have
$\tau \in S$
, we have
 $$ \begin{align} p_k(t/\unicode{x3bb}^k) \leq kB\unicode{x3bb}^{2k}\sum_{\tau\in S}\bigg(\frac{t^{1/k}}{\unicode{x3bb}}\bigg)^{|\tau|} = kB\unicode{x3bb}^{2k}p\bigg(\frac{t^{1/k}}{\unicode{x3bb}}\bigg). \end{align} $$
$$ \begin{align} p_k(t/\unicode{x3bb}^k) \leq kB\unicode{x3bb}^{2k}\sum_{\tau\in S}\bigg(\frac{t^{1/k}}{\unicode{x3bb}}\bigg)^{|\tau|} = kB\unicode{x3bb}^{2k}p\bigg(\frac{t^{1/k}}{\unicode{x3bb}}\bigg). \end{align} $$
Proof of Theorem 1
The constants A, B, and D depend on the underlying shift
![]() $\Sigma $
but do not change upon replacing
$\Sigma $
but do not change upon replacing
![]() $\Sigma $
by
$\Sigma $
by
![]() $\Sigma _k$
. Set
$\Sigma _k$
. Set
![]() $C=DA^{-1}B$
and suppose that
$C=DA^{-1}B$
and suppose that
We may apply Lemma 3 as in the previous section but now to
![]() $\Sigma _k$
to create at least
$\Sigma _k$
to create at least
![]() $AD^{-1}\unicode{x3bb} ^{km}(1-r)^m$
words of length m in
$AD^{-1}\unicode{x3bb} ^{km}(1-r)^m$
words of length m in
![]() $\Sigma _k$
, and thus words of length
$\Sigma _k$
, and thus words of length
![]() $km$
in
$km$
in
![]() $\Sigma $
, that avoid S. The entropy of
$\Sigma $
, that avoid S. The entropy of
![]() $\Sigma \langle S\rangle $
is therefore at least
$\Sigma \langle S\rangle $
is therefore at least
as desired.
5 Growing words
Let
![]() $\ell $
denote the minimal length of an element of S. Then
$\ell $
denote the minimal length of an element of S. Then
for
![]() $t\in (1,\unicode{x3bb} ^k)$
, so we consider
$t\in (1,\unicode{x3bb} ^k)$
, so we consider
This function is minimized at
 $$ \begin{align*} t_{\mathrm{\min}}=\unicode{x3bb}^{k}\frac{\unicode{x3bb}^{-2k^2/\ell}}{((\ell-k)C|S|)^{k/\ell}} \end{align*} $$
$$ \begin{align*} t_{\mathrm{\min}}=\unicode{x3bb}^{k}\frac{\unicode{x3bb}^{-2k^2/\ell}}{((\ell-k)C|S|)^{k/\ell}} \end{align*} $$
and has minimum
 $$ \begin{align*} r_{\mathrm{\min}}=C^{k/\ell}|S|^{k/\ell}\ell^{k/\ell}\bigg(1-\frac{k}{\ell}\bigg)^{k/\ell-1} \unicode{x3bb}^{-k+2k^2/\ell}. \end{align*} $$
$$ \begin{align*} r_{\mathrm{\min}}=C^{k/\ell}|S|^{k/\ell}\ell^{k/\ell}\bigg(1-\frac{k}{\ell}\bigg)^{k/\ell-1} \unicode{x3bb}^{-k+2k^2/\ell}. \end{align*} $$
Note that
![]() $t_{\mathrm {\min }}\in (1,\unicode{x3bb} ^k)$
as long as
$t_{\mathrm {\min }}\in (1,\unicode{x3bb} ^k)$
as long as
Let
![]() $\alpha \in (0,1/2)$
and set
$\alpha \in (0,1/2)$
and set
![]() $k = \lfloor \alpha \ell \rfloor $
. Simple estimates show
$k = \lfloor \alpha \ell \rfloor $
. Simple estimates show
Since
![]() $\unicode{x3bb} ^{\ell -2k}\geq \unicode{x3bb} ^{\ell (1-2\alpha )}$
, condition (6) is satisfied as long as
$\unicode{x3bb} ^{\ell -2k}\geq \unicode{x3bb} ^{\ell (1-2\alpha )}$
, condition (6) is satisfied as long as
Suppose that
![]() $|S|$
is bounded as
$|S|$
is bounded as
![]() $\ell \to \infty $
. Then (7) holds for
$\ell \to \infty $
. Then (7) holds for
![]() $\ell $
sufficiently large, and we have
$\ell $
sufficiently large, and we have
![]() $r_{\mathrm {\min }}\to 0$
. Since
$r_{\mathrm {\min }}\to 0$
. Since
![]() $-\log (1-x) = O(x)$
for small x, Theorem 1 gives
$-\log (1-x) = O(x)$
for small x, Theorem 1 gives
Setting
![]() $\alpha =1/4$
gives the best such bound, namely
$\alpha =1/4$
gives the best such bound, namely
![]() $O(\ell ^{-3/4}\unicode{x3bb} ^{-\ell /8})$
, though we note that it is possible to improve this result slightly by using more refined estimates for
$O(\ell ^{-3/4}\unicode{x3bb} ^{-\ell /8})$
, though we note that it is possible to improve this result slightly by using more refined estimates for
![]() $p_k$
in the previous section.
$p_k$
in the previous section.
Now suppose that
![]() $|S|$
may be growing but subject to
$|S|$
may be growing but subject to
![]() $|S|=O(\kappa ^\ell )$
for some
$|S|=O(\kappa ^\ell )$
for some
![]() $\kappa <\unicode{x3bb} $
. If we choose
$\kappa <\unicode{x3bb} $
. If we choose
![]() $\alpha $
small enough so that
$\alpha $
small enough so that
![]() $\kappa <\unicode{x3bb} ^{1-2\alpha }$
, then condition (7) is satisfied for
$\kappa <\unicode{x3bb} ^{1-2\alpha }$
, then condition (7) is satisfied for
![]() $\ell $
sufficiently large. We have
$\ell $
sufficiently large. We have
 $$ \begin{align*} r_{\mathrm{\min}} = O(\kappa^{\alpha\ell}\ell^\alpha\unicode{x3bb}^{-\ell\alpha(1-2\alpha)}) = O\bigg( \bigg(\frac{\kappa}{\unicode{x3bb}^{1-2\alpha}}\bigg)^{\alpha \ell}\ell^\alpha\bigg)\to 0 \end{align*} $$
$$ \begin{align*} r_{\mathrm{\min}} = O(\kappa^{\alpha\ell}\ell^\alpha\unicode{x3bb}^{-\ell\alpha(1-2\alpha)}) = O\bigg( \bigg(\frac{\kappa}{\unicode{x3bb}^{1-2\alpha}}\bigg)^{\alpha \ell}\ell^\alpha\bigg)\to 0 \end{align*} $$
as
![]() $\ell \to \infty $
, so we may once again apply Theorem 1 to obtain
$\ell \to \infty $
, so we may once again apply Theorem 1 to obtain
 $$ \begin{align*} h(\Sigma) - h(\Sigma\langle S\rangle) = O\bigg( \bigg(\frac{\kappa}{\unicode{x3bb}^{1-2\alpha}}\bigg)^{\alpha \ell}\ell^{\alpha-1}\bigg)\to 0, \end{align*} $$
$$ \begin{align*} h(\Sigma) - h(\Sigma\langle S\rangle) = O\bigg( \bigg(\frac{\kappa}{\unicode{x3bb}^{1-2\alpha}}\bigg)^{\alpha \ell}\ell^{\alpha-1}\bigg)\to 0, \end{align*} $$
thereby establishing Theorem 2.