Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T04:22:04.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy and variational principle for one-dimensional lattice systems with a general a priori probability: positive and zero temperature

Published online by Cambridge University Press:  03 July 2014

A. O. LOPES ,
J. K. MENGUE ,
J. MOHR  and
R. R. SOUZA
A. O. LOPES
Affiliation:
Instituto de Matemática, UFRGS - Porto Alegre, Brazil email [email protected]
J. K. MENGUE
Affiliation:
Instituto de Matemática, UFRGS - Porto Alegre, Brazil email [email protected]
J. MOHR
Affiliation:
Instituto de Matemática, UFRGS - Porto Alegre, Brazil email [email protected]
R. R. SOUZA
Affiliation:
Instituto de Matemática, UFRGS - Porto Alegre, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We generalize several results of the classical theory of thermodynamic formalism by considering a compact metric space 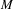$M$ as the state space. We analyze the shift acting on 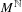$M^{\mathbb{N}}$ and consider a general a priori probability for defining the transfer (Ruelle) operator. We study potentials $A$ which can depend on the infinite set of coordinates in 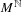$M^{\mathbb{N}}$. We define entropy and by its very nature it is always a non-positive number. The concepts of entropy and transfer operator are linked. If 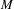$M$ is not a finite set there exist Gibbs states with arbitrary negative value of entropy. Invariant probabilities with support in a fixed point will have entropy equal to minus infinity. In the case 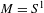$M=S^{1}$, and the a priori measure is Lebesgue 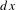$dx$, the infinite product of 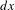$dx$ on 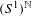$(S^{1})^{\mathbb{N}}$ will have zero entropy. We analyze the Pressure problem for a Hölder potential $A$ and its relation with eigenfunctions and eigenprobabilities of the Ruelle operator. Among other things we analyze the case where temperature goes to zero and we show some selection results. Our general setting can be adapted in order to analyze the thermodynamic formalism for the Bernoulli space with countable infinite symbols. Moreover, the so-called 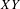$XY$ model also fits under our setting. In this last case 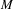$M$ is the unitary circle 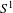$S^{1}$. We explore the differentiable structure of 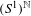$(S^{1})^{\mathbb{N}}$ by considering a certain class of smooth potentials and we show some properties of the corresponding main eigenfunctions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 6 , September 2015 , pp. 1925 - 1961
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asaoka, M., Fukaya, T., Mitsui, K. and Tsukamoto, M.. Growth of critical points in one-dimensional lattice systems. Preprint, 2012.Google Scholar
Baraviera, A., Lopes, A. O. and Thieullen, P.. A large deviation principle for equilibrium states of Hölder potentials: the zero temperature case. Stoch. Dynam. 6 (2006), 77–96.CrossRefGoogle Scholar
Baraviera, A. T., Cioletti, L., Lopes, A. O., Mohr, J. and Souza, R. R.. On the general one-dimensional XY model: positive and zero temperature, selection and non-selection. Rev. Math. Phys. 23(10) (2011), 1063–1113 82Bxx.CrossRefGoogle Scholar
Baraviera, A. T., Lopes, A. O. and Mengue, J. K.. On the selection of subaction and measure for a subclass of potentials defined by P. Walters. Ergod. Th. & Dynam. Sys. 33(5) (2013), 1338–1362.CrossRefGoogle Scholar
Bernard, P. and Contreras, G.. A generic property of families of Lagrangian systems. Ann. of Math. 167(3) (2008), 1099–1108.CrossRefGoogle Scholar
Bertelson, M.. Topological invariant for discrete group actions. Lett. Math. Phys. 62 (2004), 147–156.CrossRefGoogle Scholar
Bertelson, M. and Gromov, M.. Dynamical Morse entropy. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 27–44.Google Scholar
Bissacot, R. and Freire, R. Jr. On the existence of maximizing measures for irreducible countable Markov shifts: a dynamical proof. Ergod. Th. & Dynam. Sys. to appear.Google Scholar
Bissacot, R. and Garibaldi, E.. Weak KAM methods and ergodic optimal problems for countable Markov shifts. Bull. Braz. Math. Soc. 41(3) (2010), 321–338.CrossRefGoogle Scholar
Bousch, T.. La condition de Walters. Ann. Sci. Éc. Norm. Super. (4) 34(2) (2001), 287–311.CrossRefGoogle Scholar
Chazottes, J.R., Gambaudo, J.M. and Ulgade, E.. Zero-temperature limit of one dimensional Gibbs states via renormalization: the case of locally constant potentials. Ergod. Th. & Dynam. Sys. 31(4) (2011), 1109–1161.CrossRefGoogle Scholar
Chazottes, J. R. and Hochman, M.. On the zero-temperature limit of Gibbs states. Commun. Math. Phys. 297(N1) (2010), 265–281.CrossRefGoogle Scholar
Chou, W. and Duffin, R. J.. An additive eigenvalue problem of physics related to linear programming. Adv. Appl. Math. 8 (1987), 486–498.CrossRefGoogle Scholar
Chou, W. and Griffiths, R.. Ground states of one-dimensional systems using effective potentials. Phys. Rev. B 34(9) (1986), 6219–6234.CrossRefGoogle ScholarPubMed
Contreras, G. and Iturriaga, R.. Global Minimizers of Autonomous Lagrangians (22° Colóquio Brasileiro de Matemática). IMPA, Rio de Janeiro, 1999.Google Scholar
Contreras, G., Lopes, A. and Oliveira, E.. Ergodic transport theory, periodic maximizing probabilities and the twist condition. Modeling, Optimization, Dynamics and Bioeconomy (Proceedings in Mathematics). Eds. Zilberman, D. and Pinto, A.. Springer, to appear.Google Scholar
Contreras, G., Lopes, A. O. and Thieullen, Ph.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1379–1409.Google Scholar
Conze, J. P. and Guivarc’h, Y.. Croissance des sommes ergodiques et principe variationnel. Manuscript circa 1993.Google Scholar
Daon, Y.. Bernoullicity of equilibrium measures on countable Markov shifts. Discrete Contin. Dyn. Syst. 33(9) (2013), 4003–4015.CrossRefGoogle Scholar
Ellis, R.. Entropy, Large Deviations, and Statistical Mechanics. Springer, Berlin, 2005.Google Scholar
Fathi, A.. Théor\`eme KAM faible et théorie de Mather sur les syst\`emes lagrangiens. C. R. Acad. Sci. Sér. I Math. 324 (1997), 1043–1046.Google Scholar
Fukaya, T. and Tsukamoto, M.. Asymptotic distribution of critical values. Geom. Dedicata 143 (2009), 63–67.CrossRefGoogle Scholar
Fukui, Y. and Horiguchi, M.. One-dimensional Chiral XY Model at finite temperature. Interdisciplinary Inf. Sci. 1(2) (1995), 133–149.Google Scholar
Gallavotti, G.. Statistical Mechanics: A Short Treatise. Springer, Berlin, 2010.Google Scholar
Garibaldi, E. and Lopes, A. O.. On Aubry–Mather theory for symbolic dynamics. Ergod. Th. & Dynam. Sys. 28(3) (2008), 791–815.CrossRefGoogle Scholar
Garibaldi, E. and Lopes, A. O.. The effective potential and transshipment in thermodynamic formalism at temperature zero. Stoch. Dyn. 13(1) (2013),1250009.CrossRefGoogle Scholar
Georgii, H.-O.. Gibbs Measures and Phase Transitions. de Gruyter, Berlin, 1988.CrossRefGoogle Scholar
Gomes, D. A., Lopes, A. O. and Mohr, J.. The Mather measure and a large deviation principle for the entropy penalized method. Commun. Contemp. Math. 13(2) (2011), 235–268.CrossRefGoogle Scholar
Gomes, D. A. and Valdinoci, E.. Entropy penalization methods for Hamilton–Jacobi equations. Adv. Math. 215(1) (2007), 94–152.CrossRefGoogle Scholar
Gromov, M.. Singularities, expanders and topology of maps. Part 2: From combinatorics to topology via algebraic isoperimetry. Geom. Funct. Anal. 20(2) (2010), 416–526.CrossRefGoogle Scholar
Iommi, G.. Ergodic optimization for renewal type shifts. Monatsh. Math. 150(2) (2007), 91–95.CrossRefGoogle Scholar
Israel, R. B.. Convexity in the Theory of Lattice Gases. Princeton University Press, Princeton, NJ, 1979.Google Scholar
Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. Ser. A 15 (2006), 197–224.CrossRefGoogle Scholar
Jenkinson, O., Mauldin, R. D. and Urbanski, M.. Zero temperature limits of Gibbs-equilibrium states for countable alphabet subshifts of finite type. J. Stat. Phys. 119(3–4) (2005), 765–776.CrossRefGoogle Scholar
Keller, G.. Gibbs States in Ergodic Theory. Cambridge University Press, Cambridge, 1998.Google Scholar
Kempton, T.. Zero temperature limits of Gibbs equilibrium states for countable markov shifts. J. Stat. Phys. 143 (2011), 795–806.CrossRefGoogle Scholar
Lanford, O.. Entropy and equilibrium states in classical statistical mechanics. Statistical Mechanics and Mathematical Problems (Battelle Rencontres, Seattle, WA, 1971) (Lecture Notes in Physics, 20). Springer, Berlin, 1973.Google Scholar
Leplaideur, R.. A dynamical proof for convergence of Gibbs measures at temperature zero. Nonlinearity 18(6) (2005), 2847–2880.CrossRefGoogle Scholar
Lopes, A. and Mengue, J.. Duality theorems in ergodic transport. J. Stat. Phys. 149(5) (2012), 921–942.CrossRefGoogle Scholar
Lopes, A. and Mengue, J.. Selection of measure and a large deviation principle for the general one-dimensional XY model. Dyn. Syst. 29(1) (2014), 24–39.CrossRefGoogle Scholar
Lopes, A. and Thieullen, P.. Subactions for Anosov flows. Ergod. Th. & Dynam. Sys. 25(2) (2005), 605–628.CrossRefGoogle Scholar
Lopes, A. and Thieullen, P.. Subactions for Anosov diffeomorphisms. Asterisque Geom. Dynam. (II) 287 (2013), 135–146.Google Scholar
Lopes, A. O.. An analogy of charge distribution on Julia sets with the Brownian motion. J. Math. Phys. 30(9) (1989), 2120–2124.CrossRefGoogle Scholar
Lopes, A. O. and Mengue, J.. Zeta measures and thermodynamic formalism for temperature zero. Bull. Braz. Math. Soc. 41(3) (2010), 449–480.CrossRefGoogle Scholar
Lopes, A. O., Mohr, J., Souza, R. and Thieullen, Ph.. Negative entropy, zero temperature and stationary Markov chains on the interval. Bull. Braz. Math. Soc. 40 (2009), 1–52.CrossRefGoogle Scholar
Lopes, A. O., Neumann, A. and Thieullen, Ph.. A thermodynamic formalism for continuous time Markov chains with values on the Bernoulli space: entropy, pressure and large deviations. J. Stat. Phys. 152(5) (2013), 894–933.CrossRefGoogle Scholar
Lopes, A. O. and Oliveira, E.. Entropy and variational principles for holonomic probabilities of IFS. Discrete Cont. Dyn. Syst. A 23(3) (2009), 937–955.CrossRefGoogle Scholar
Lopes, A. O., Oliveira, E. R. and Thieullen, Ph.. The dual potential, the involution kernel and transport in ergodic optimization. Preprint, 2008.Google Scholar
Mañé, R.. The Hausdorff Dimension of Invariant Probabilities of Rational Maps (Lecture Notes in Mathematics, 1331). Springer, Berlin, 1988, pp. 86–117.Google Scholar
Mayer, D. H.. The Ruelle–Araki Transfer Operator in Classical Statistical Mechanics (Lecture Notes in Physics, 123). Springer, Berlin, 1980.Google Scholar
Morris, I. D.. Entropy for zero-temperature limits of Gibbs-equilibrium states for countable-alphabet subshifts of finite type. J. Stat. Phys. 126(2) (2007), 315–324.CrossRefGoogle Scholar
Parry, W. and Pollicott, M.. Zeta Functions and the Periodic Orbit Structure of Hyperbolic Dynamics (Astérisque, 187–188). Societé Mathématique de France, Paris, 1990.Google Scholar
Pollicott, M. and Yuri, M.. Dynamical Systems and Ergodic Theory. Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic Formalism, 2nd edn. Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
Sarig, O.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19 (1999), 1565–1593.CrossRefGoogle Scholar
Sarig, O.. Thermodynamic formalism for topological Markov shifts. Lecture Notes. Penn State, 2009.Google Scholar
Simon, B.. The Statistical Mechanics of Lattice Gases. Princeton University Press, Princeton, NJ, 1993.Google Scholar
Souza, R. R.. Sub-actions for weakly hyperbolic one-dimensional systems. Dynam. Syst. 2(18) (2003), 165–179.CrossRefGoogle Scholar
Thompson, C.. Infinite-spin Ising model in one dimension. J. Math. Phys. 9(2) (1968), 241–245.CrossRefGoogle Scholar
van Enter, A. C. D., Fernandez, R. and Sokal, A. D.. Regularity properties and pathologies of position-space renormalization-group transformations: scope and limitations of Gibbsian theory. J. Stat. Phys. 72(5/6) (1993), 879–1187.CrossRefGoogle Scholar
van Enter, A. C. D. and Ruszel, W. M.. Chaotic temperature dependence at zero temperature. J. Stat. Phys. 127(3) (2007), 567–573.CrossRefGoogle Scholar