Entropy and its variational principle for locally compact metrizable systems

Abstract

For a given topological dynamical system 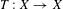$T:X\rightarrow X$ over a compact set 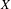$X$ with a metric 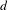$d$, the variational principle states that

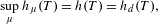$$\begin{eqnarray}\sup _{\unicode[STIX]{x1D707}}h_{\unicode[STIX]{x1D707}}(T)=h(T)=h_{d}(T),\end{eqnarray}$$

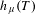where $h_{\unicode[STIX]{x1D707}}(T)$ is the Kolmogorov–Sinai entropy with the supremum taken over every $T$-invariant probability measure, 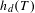$h_{d}(T)$ is the Bowen entropy and 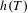$h(T)$ is the topological entropy as defined by Adler, Konheim and McAndrew. In Patrão [Entropy and its variational principle for non-compact metric spaces. Ergod. Th. & Dynam. Sys. 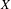30 (2010), 1529–1542], the concept of topological entropy was adapted for the case where $T$ is a proper map and $X$ is locally compact separable and metrizable, and the variational principle was extended to

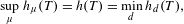$$\begin{eqnarray}\sup _{\unicode[STIX]{x1D707}}h_{\unicode[STIX]{x1D707}}(T)=h(T)=\min _{d}h_{d}(T),\end{eqnarray}$$

where the minimum is taken over every distance compatible with the topology of $X$. In the present work, we drop the properness assumption and extend the above result for any continuous map $T$. We also apply our results to extend some previous formulae for the topological entropy of continuous endomorphisms of connected Lie groups that were proved in Caldas and Patrão [Dynamics of endomorphisms of Lie groups. Discrete Contin. Dyn. Syst. 33 (2013). 1351–1363]. In particular, we prove that any linear transformation 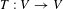$T:V\rightarrow V$ over a finite-dimensional vector space $V$ has null topological entropy.