Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-24T20:03:13.533Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropies and volume growth of unstable manifolds

Part of: Ergodic theory Measure-theoretic ergodic theory

Published online by Cambridge University Press:  04 February 2021

YUNTAO ZANG
YUNTAO ZANG*
Affiliation:
School of Mathematical Sciences, East China Normal University, Shanghai200062, P.R. China (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let f be a 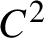$C^2$ diffeomorphism on a compact manifold. Ledrappier and Young introduced entropies along unstable foliations for an ergodic measure 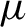$\mu $ . We relate those entropies to covering numbers in order to give a new upper bound on the metric entropy of 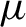$\mu $ in terms of Lyapunov exponents and topological entropy or volume growth of sub-manifolds. We also discuss extensions to the 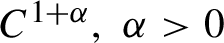$C^{1+\alpha },\,\alpha>0$ , case.

Keywords

entropyLyapunov exponentsvolume growth

MSC classification

Primary: 37A35: Entropy and other invariants, isomorphism, classification 28D20: Entropy and other invariants
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 4 , April 2022 , pp. 1576 - 1590
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, A.. Smoothness of holonomies inside center-stable manifolds and the ${C}^2$ hypothesis in Pugh–Shub and Ledrappier–Young theory. Preprint, 2016, arXiv:1608.05886.Google Scholar
Buzzi, J.. Dimensional entropies and semi-uniform hyperbolicity. New Trends in Mathematical Physics: Selected Contributions of the XVth International Congress on Mathematical Physics. Ed. Sidoravicius, V.. Springer, Dordrecht, 2009, pp. 95–116.CrossRefGoogle Scholar
Cogswell, K.. Entropy and volume growth. Ergod. Th. & Dynam. Sys. 20 (2000), 77–84.CrossRefGoogle Scholar
Fathi, A., Herman, M.-R. and Yoccoz, J.-C.. A proof of Pesin’s stable manifold theorem. Geometric Dynamics (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 177–215.CrossRefGoogle Scholar
Guo, X., Liao, G., Sun, W. and Yang, D.. On the hybrid control of metric entropy for dominated splittings. Discrete Contin. Dyn. Syst. 38 (2018), 5011–5019.CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Katok, A., Strelcyn, J., Ledrappier, F. and Przytycki, F.. Invariant Manifolds, Entropy and Billiards; Smooth Maps with Singularities (Lecture Notes in Mathematics, 1222). Springer, Berlin, 1986.CrossRefGoogle Scholar
Kozlovski, O. S.. An integral formula for topological entropy of ${C}^{\infty }$ maps. Ergod. Th. & Dynam. Sys. 18 (1998), 405–424.CrossRefGoogle Scholar
Ledrappier, F. and Strelcyn, J.. A proof of the estimation from below in Pesin’s entropy formula. Ergod. Th. & Dynam. Sys. 2(1982), 203–219.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. I. Characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. 122 (1985), 505–539.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension. Ann. of Math. 122(1985), 540–574.CrossRefGoogle Scholar
Newhouse, S. E.. Entropy and volume. Ergod. Th. & Dynam. Sys. 8 (1988), 283–299.Google Scholar
Oseledec, V. I.. A multiplicative ergodic theorem. Characteristic Ljapunov exponents of dynamical systems. Trudy Moskov. Mat. Obšč. 19 (1968), 179–210.Google Scholar
Przytycki, F.. An upper estimation for topological entropy of diffeomorphisms. Invent. Math. 59 (1980), 205–213.CrossRefGoogle Scholar
Rohlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Translations 1952 (1952), 55.Google Scholar
Rohlin, V. A.. Lectures on the entropy theory of measure-preserving transformations. Russian Math. Surveys 22 (1967), 1–52.CrossRefGoogle Scholar
Ruelle, D.. An inequality for the entropy of differentiable maps. Bull. Braz. Math. Soc. (N.S.) 8 (1978), 83–88.CrossRefGoogle Scholar
Saghin, R.. Volume growth and entropy for ${C}^1$ partially hyperbolic diffeomorphisms. Discrete Contin. Dyn. Syst. 34 (2014), 3789–3801.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer, New York, 1982.CrossRefGoogle Scholar