Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:49:38.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamics of postcritically bounded polynomial semigroups III: classification of semi-hyperbolic semigroups and random Julia sets which are Jordan curves but not quasicircles

Published online by Cambridge University Press:  17 March 2010

HIROKI SUMI
HIROKI SUMI*
Affiliation:
Department of Mathematics, Graduate School of Science, Osaka University, 1-1, Machikaneyama, Toyonaka, Osaka, 560-0043, Japan (email: [email protected])http://www.math.sci.osaka-u.ac.jp/∼sumi/
Get access Rights & Permissions [Opens in a new window]

Abstract

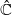We investigate the dynamics of polynomial semigroups (semigroups generated by a family of polynomial maps on the Riemann sphere ) and the random dynamics of polynomials on the Riemann sphere. Combining the dynamics of semigroups and the fiberwise (random) dynamics, we give a classification of polynomial semigroups G such that G is generated by a compact family Γ, the planar postcritical set of G is bounded, and G is (semi-) hyperbolic. In one of the classes, we have that, for almost every sequence 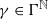, the Julia set Jγ of γ is a Jordan curve but not a quasicircle, the unbounded component of 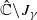is a John domain, and the bounded component of 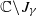is not a John domain. Note that this phenomenon does not hold in the usual iteration of a single polynomial. Moreover, we consider the dynamics of polynomial semigroups G such that the planar postcritical set of G is bounded and the Julia set is disconnected. Those phenomena of polynomial semigroups and random dynamics of polynomials that do not occur in the usual dynamics of polynomials are systematically investigated.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 6 , December 2010 , pp. 1869 - 1902
Copyright
Copyright © Cambridge University Press 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Brück, R.. Geometric properties of Julia sets of the composition of polynomials of the form z 2+c n. Pacific J. Math. 198(2) (2001), 347–372.CrossRefGoogle Scholar
[2]Brück, R., Büger, M. and Reitz, S.. Random iterations of polynomials of the form z 2+c n: connectedness of Julia sets. Ergod. Th. & Dynam. Sys. 19(5) (1999), 1221–1231.CrossRefGoogle Scholar
[3]Büger, M.. Self-similarity of Julia sets of the composition of polynomials. Ergod. Th. & Dynam. Sys. 17 (1997), 1289–1297.CrossRefGoogle Scholar
[4]Büger, M.. On the composition of polynomials of the form z2+cn. Math. Ann. 310(4) (1998), 661–683.Google Scholar
[5]Carleson, L., Jones, P. W. and Yoccoz, J.-C.. Julia and John. Bol. Soc. Brasil. Mat. (N.S.) 25(1) (1994), 1–30.CrossRefGoogle Scholar
[6]DeMarco, L. and Hruska, S. L.. Axiom A polynomial skew products of and their postcritical sets. Ergod. Th. & Dynam. Sys. 28 (2008), 1749–1779.CrossRefGoogle Scholar
[7]DeMarco, L. and Hruska, S. L.. Correction to Axiom A polynomial skew products of ℂ2 and their postcritical sets. Preprint, http://www.math.uic.edu/∼demarko/correction.pdf.Google Scholar
[8]Devaney, R.. An Introduction to Chaotic Dynamical Systems, 2nd edn. Perseus Books, Reading, MA, 1989.Google Scholar
[9]Fornaess, J. E. and Sibony, N.. Random iterations of rational functions. Ergod. Th. & Dynam. Sys. 11 (1991), 687–708.CrossRefGoogle Scholar
[10]Gong, Z., Qiu, W. and Li, Y.. Connectedness of Julia sets for a quadratic random dynamical system. Ergod. Th. & Dynam. Sys. 23 (2003), 1807–1815.CrossRefGoogle Scholar
[11]Gong, Z. and Ren, F.. A random dynamical system formed by infinitely many functions. J. Fudan Univ., Nat. Sci. 35 (1996), 387–392.Google Scholar
[12]Hinkkanen, A. and Martin, G. J.. The dynamics of semigroups of rational functions I. Proc. Lond. Math. Soc. (3) 73 (1996), 358–384.CrossRefGoogle Scholar
[13]Hinkkanen, A. and Martin, G. J.. Julia sets of rational semigroups. Math. Z. 222(2) (1996), 161–169.CrossRefGoogle Scholar
[14]Jonsson, M.. Ergodic properties of fibered rational maps. Ark. Mat. 38 (2000), 281–317.CrossRefGoogle Scholar
[15]Lehto, O. and Virtanen, K. I.. Quasiconformal Mappings in the Plane. Springer, Berlin, 1973.CrossRefGoogle Scholar
[16]Milnor, J.. Dynamics in One Complex Variable, 3rd edn.(Annals of Mathematical Studies, 160). Princeton University Press, Princeton, NJ, 2006.Google Scholar
[17]Näkki, R. and Väisälä, J.. John discs. Expo. math. 9 (1991), 3–43.Google Scholar
[18]Pilgrim, K. and Lei, T.. Rational maps with disconnected Julia set. Astérisque 261 (2000), 349–384.Google Scholar
[19]Sester, O.. Hyperbolicité des polynômes fibrés. Bull. Soc. Math. France 127(3) (1999), 393–428.CrossRefGoogle Scholar
[20]Stankewitz, R.. Completely invariant Julia sets of polynomial semigroups. Proc. Amer. Math. Soc. 127(10) (1999), 2889–2898.CrossRefGoogle Scholar
[21]Stankewitz, R.. Completely invariant sets of normality for rational semigroups. Complex Variables, Theory Appl. 40 (2000), 199–210.Google Scholar
[22]Stankewitz, R.. Uniformly perfect sets, rational semigroups, Kleinian groups and IFS’s. Proc. Amer. Math. Soc. 128(9) (2000), 2569–2575.CrossRefGoogle Scholar
[23]Stankewitz, R., Sugawa, T. and Sumi, H.. Some counterexamples in dynamics of rational semigroups. Ann. Acad. Sci. Fenn. Math. 29 (2004), 357–366.Google Scholar
[24]Stankewitz, R. and Sumi, H.. Dynamical properties and structure of Julia sets of postcritically bounded polynomial semigroups. Trans. Amer. Math. Soc. to appear, http://arxiv.org/abs/0708.3187.Google Scholar
[25]Steinmetz, N.. Rational Iteration (de Gruyter Studies in Mathematics, 16). Walter de Gruyter, Berlin, New York, 1993.CrossRefGoogle Scholar
[26]Steinsaltz, D.. Random logistic maps Lyapunov exponents. Indag. Math. (N.S.) 12(4) (2001), 557–584.CrossRefGoogle Scholar
[27]Sumi, H.. Dynamics of sub-hyperbolic and semi-hyperbolic rational semigroups and skew products. Ergod. Th. & Dynam. Sys. 21 (2001), 563–603.CrossRefGoogle Scholar
[28]Sumi, H.. A correction to the proof of a lemma in ‘Dynamics of sub-hyperbolic and semi-hyperbolic rational semigroups and skew products’. Ergod. Th. & Dynam. Sys. 21 (2001), 1275–1276.Google Scholar
[29]Sumi, H.. Skew product maps related to finitely generated rational semigroups. Nonlinearity 13 (2000), 995–1019.CrossRefGoogle Scholar
[30]Sumi, H.. Semi-hyperbolic fibered rational maps and rational semigroups. Ergod. Th. & Dynam. Sys. 26 (2006), 893–922.CrossRefGoogle Scholar
[31]Sumi, H.. Erratum to: ‘Semi-hyperbolic fibered rational maps and rational semigroups’ [Ergod. Th. & Dynam. Sys. 26(3) (2006), 893–922]. Ergod. Th. & Dynam. Sys. 28(3) (2008), 1043–1045.Google Scholar
[32]Sumi, H.. On dynamics of hyperbolic rational semigroups. J. Math. Kyoto Univ. 37(4) (1997), 717–733.Google Scholar
[33]Sumi, H.. Dimensions of Julia sets of expanding rational semigroups. Kodai Math. J. 28(2) (2005), 390–422. (See also http://arxiv.org/abs/math.DS/0405522.)CrossRefGoogle Scholar
[34]Sumi, H.. Random dynamics of polynomials and devil’s-staircase-like functions in the complex plane. Appl. Math. Comput. 187 (2007), 489–500. (Proceedings paper of a conference.)Google Scholar
[35]Sumi, H.. The space of postcritically bounded 2-generator polynomial semigroups with hyperbolicity. RIMS Kokyuroku 1494 (2006), 62–86. (Proceedings paper.)Google Scholar
[36]Sumi, H.. Interaction cohomology of forward or backward self-similar systems. Adv. Math. 222(3) (2009), 729–781.CrossRefGoogle Scholar
[37]Sumi, H.. Dynamics of postcritically bounded polynomial semigroups I: connected components of the Julia sets. Preprint, 2008, http://arxiv.org/abs/0811.3664.Google Scholar
[38]Sumi, H.. Dynamics of postcritically bounded polynomial semigroups II: fiberwise dynamics and the Julia sets. Preprint, 2008.Google Scholar
[39]Sumi, H.. Random complex dynamics and semigroups of holomorphic maps. Preprint, 2008, http://arxiv.org/abs/0812.4483.Google Scholar
[40]Sumi, H.. In preparation.Google Scholar
[41]Sumi, H. and Urbański, M.. The equilibrium states for semigroups of rational maps. Monatsh. Math. 156(4) (2009), 371–390.CrossRefGoogle Scholar
[42]Sumi, H. and Urbański, M.. Real analyticity of Hausdorff dimension for expanding rational semigroups. Ergod. Th. & Dynam. Sys. to appear, http://arxiv.org/abs/0707.2447.Google Scholar
[43]Sumi, H. and Urbański, M.. Measures and dimensions of Julia sets of semi-hyperbolic rational semigroups. Preprint, 2008, http://arxiv.org/abs/0811.1809.Google Scholar
[44]Sun, Y. and Yang, C.-C.. On the connectivity of the Julia set of a finitely generated rational semigroup. Proc. Amer. Math. Soc. 130(1) (2001), 49–52.CrossRefGoogle Scholar
[45]Zhou, W. and Ren, F.. The Julia sets of the random iteration of rational functions. Chinese Sci. Bull. 37(12) (1992), 969–971.Google Scholar