Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T20:09:57.619Z Has data issue: false hasContentIssue false
  • English
  • Français

The dynamical zeta function for commuting automorphisms of zero-dimensional groups

Published online by Cambridge University Press:  08 November 2016

RICHARD MILES  and
THOMAS WARD
RICHARD MILES
Affiliation:
MASH, University of Sheffield, Sheffield S10 2TN, UK email [email protected]
THOMAS WARD
Affiliation:
Level 13 Ziff Building, University of Leeds, LeedsLS2 9JT, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a 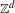$\mathbb{Z}^{d}$-action $\unicode[STIX]{x1D6FC}$ by commuting homeomorphisms of a compact metric space, Lind introduced a dynamical zeta function that generalizes the dynamical zeta function of a single transformation. In this article, we investigate this function when $\unicode[STIX]{x1D6FC}$ is generated by continuous automorphisms of a compact abelian zero-dimensional group. We address Lind’s conjecture concerning the existence of a natural boundary for the zeta function and prove this for two significant classes of actions, including both zero entropy and positive entropy examples. The finer structure of the periodic point counting function is also examined and, in the zero entropy case, we show how this may be severely restricted for subgroups of prime index in 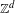$\mathbb{Z}^{d}$. We also consider a related open problem concerning the appearance of a natural boundary for the dynamical zeta function of a single automorphism, giving further weight to the Pólya–Carlson dichotomy proposed by Bell and the authors.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1564 - 1587
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artin, M. and Mazur, B.. On periodic points. Ann. of Math. (2) 81 (1965), 82–99.Google Scholar
Bell, J., Miles, R. and Ward, T.. Towards a Pólya–Carlson dichotomy for algebraic dynamics. Indag. Math. (N.S.) 25(4) (2014), 652–668.Google Scholar
Carlson, F.. Über ganzwertige Funktionen. Math. Z. 11(1–2) (1921), 1–23.Google Scholar
Choie, Y., Lichiardopol, N., Moree, P. and Solé, P.. On Robin’s criterion for the Riemann hypothesis. J. Théor. Nombres Bordeaux 19(2) (2007), 357–372.Google Scholar
Chothi, V., Everest, G. and Ward, T.. S-integer dynamical systems: periodic points. J. Reine Angew. Math. 489 (1997), 99–132.Google Scholar
Corvaja, P. and Zannier, U.. A lower bound for the height of a rational function at S-unit points. Monatsh. Math. 144(3) (2005), 203–224.Google Scholar
Corvaja, P. and Zannier, U.. Greatest common divisors of u - 1, v - 1 in positive characteristic and rational points on curves over finite fields. J. Eur. Math. Soc. (JEMS) 15(5) (2013), 1927–1942.Google Scholar
Einsiedler, M. and Lind, D.. Algebraic ℤ d -actions of entropy rank one. Trans. Amer. Math. Soc. 356(5) (2004), 1799–1831.Google Scholar
Everest, G., van der Poorten, A., Shparlinski, I. and Ward, T.. Recurrence Sequences (Mathematical Surveys and Monographs, 104) . American Mathematical Society, Providence, RI, 2003.Google Scholar
Everest, G. and Ward, T.. Heights of polynomials and entropy in algebraic dynamics. Universitext. Springer, London, 1999.Google Scholar
Gronwall, T. H.. Some asymptotic expressions in the theory of numbers. Trans. Amer. Math. Soc. 14(1) (1913), 113–122.Google Scholar
Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9(4) (1989), 691–735.Google Scholar
Kurlberg, P. and Pomerance, C.. On the periods of the linear congruential and power generators. Acta Arith. 119(2) (2005), 149–169.Google Scholar
Ledrappier, F.. Un champ markovien peut être d’entropie nulle et mélangeant. C. R. Acad. Sci. Paris A–B 287(7) (1978), A561–A563.Google Scholar
Lidl, R. and Niederreiter, H.. Introduction to Finite Fields and their Applications, 1st edn. Cambridge University Press, Cambridge, 1994.Google Scholar
Lind, D. A.. A zeta function for ℤ d -actions. Ergodic Theory of ℤ d -actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 433–450.Google Scholar
Lind, D., Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math. 101(3) (1990), 593–629.Google Scholar
Matsumura, H.. Commutative Ring Theory, 2nd edn. (Cambridge Studies in Advanced Mathematics, 8) . Cambridge University Press, Cambridge, 1989.Google Scholar
Miles, R.. Zeta functions for elements of entropy rank-one actions. Ergod. Th. & Dyn. Sys. 27(2) (2007), 567–582.Google Scholar
Miles, R.. Periodic points of endomorphisms on solenoids and related groups. Bull. Lond. Math. Soc. 40(4) (2008), 696–704.Google Scholar
Miles, R.. Synchronization points and associated dynamical invariants. Trans. Amer. Math. Soc. 365(10) (2013), 5503–5524.Google Scholar
Miles, R.. A natural boundary for the dynamical zeta function for commuting group automorphisms. Proc. Amer. Math. Soc. 143(7) (2015), 2927–2933.Google Scholar
Pólya, G.. Über gewisse notwendige Determinantenkriterien für die Fortsetzbarkeit einer Potenzreihe. Math. Ann. 99(1) (1928), 687–706.Google Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128) . Birkhäuser, Basel, 1995.Google Scholar
Segal, S. L.. Nine Introductions in Complex Analysis (North-Holland Mathematics Studies, 208) , revised edn. Elsevier Science B.V., Amsterdam, 2008.Google Scholar
Silverman, J. H.. Common divisors of a n - 1 and b n - 1 over function fields. New York J. Math. 10 (2004), 37–43.Google Scholar
Ward, T.. Dynamical zeta functions for typical extensions of full shifts. Finite Fields Appl. 5(3) (1999), 232–239.Google Scholar