Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T01:47:02.214Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical degree, arithmetic entropy, and canonical heights for dominant rational self-maps of projective space

Published online by Cambridge University Press:  29 November 2012

JOSEPH H. SILVERMAN
JOSEPH H. SILVERMAN*
Affiliation:
Mathematics Department, Box 1917, Brown University, Providence, RI 02912, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

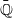Let φ:ℙN⤏ℙN be a dominant rational map. The dynamical degree of φ is the quantity δφ=lim (deg φn)1/n. When φ is defined over ${\bar {{\mathbb {Q}}}}$, we define the arithmetic degree of a point 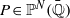$P\in {\mathbb {P}}^N({\bar {{\mathbb {Q}}}})$ to be αφ(P)=lim sup h(φn(P))1/n and the canonical height of P to be 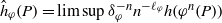$\hat {h}_\varphi (P)=\limsup \delta _\varphi ^{-n}n^{-\ell _\varphi }h(\varphi ^n(P))$ for an appropriately chosen ℓφ. We begin by proving some elementary relations and making some deep conjectures relating δφ, αφ(P) , 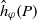${\hat h}_\varphi (P)$, and the Zariski density of the orbit 𝒪φ(P) of P. We then prove our conjectures for monomial maps.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 2 , April 2014 , pp. 647 - 678
Copyright
©2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Abarenkova, N., Anglès d’Auriac, J.-Ch., Boukraa, S., Hassani, S. and Maillard, J.-M.. Topological entropy and Arnold complexity for two-dimensional mappings. Phys. Lett. A 262(1) (1999), 44–49.Google Scholar
[2]Adler, R. L., Konheim, A. G. and McAndrew, M. H.. Topological entropy. Trans. Amer. Math. Soc. 114 (1965), 309–319.Google Scholar
[3]Amerik, E.. Existence of non-preperiodic algebraic points for a rational self-map of infinite order. Math. Res. Lett. 18(2) (2011), 251–256.Google Scholar
[4]Anglès d’Auriac, J.-Ch., Maillard, J.-M. and Viallet, C. M.. On the complexity of some birational transformations. J. Phys. A 39(14) (2006), 3641–3654.Google Scholar
[5]Arnol’d, V. I.. Dynamics of complexity of intersections. Bol. Soc. Brasil. Mat. (N.S.) 21(1) (1990), 1–10.Google Scholar
[6]Baker, A.. Transcendental Number Theory, 2nd edn.(Cambridge Mathematical Library). Cambridge University Press, Cambridge, 1990.Google Scholar
[7]Baker, M.. A finiteness theorem for canonical heights attached to rational maps over function fields. J. Reine Angew. Math. 626 (2009), 205–233.Google Scholar
[8]Bedford, E. and Kim, K.. On the degree growth of birational mappings in higher dimension. J. Geom. Anal. 14(4) (2004), 567–596.Google Scholar
[9]Bedford, E. and Kim, K.. Degree growth of matrix inversion: birational maps of symmetric, cyclic matrices. Discrete Contin. Dyn. Syst. 21(4) (2008), 977–1013.Google Scholar
[10]Bedford, E. and Kim, K.. Linear recurrences in the degree sequences of monomial mappings. Ergod. Th. & Dynam. Sys. 28(5) (2008), 1369–1375.Google Scholar
[11]Bedford, E., Kim, K., Truong, T. T., Abarenkova, N. and Maillard, J.-M.. Degree complexity of a family of birational maps. Math. Phys. Anal. Geom. 11(1) (2008), 53–71.Google Scholar
[12]Bellon, M. P. and Viallet, C.-M.. Algebraic entropy. Comm. Math. Phys. 204(2) (1999), 425–437.Google Scholar
[13]Benedetto, R. L.. Heights and preperiodic points of polynomials over function fields. Int. Math. Res. Not. (62) (2005), 3855–3866.Google Scholar
[14]Bombieri, E. and Gubler, W.. Heights in Diophantine Geometry (New Mathematical Monographs, 4). Cambridge University Press, Cambridge, 2006.Google Scholar
[15]Boucksom, S., Favre, C. and Jonsson, M.. Degree growth of meromorphic surface maps. Duke Math. J. 141(3) (2008), 519–538.CrossRefGoogle Scholar
[16]Buium, A.. Complex dynamics and invariant forms mod p. Int. Math. Res. Not. (31) (2005), 1889–1899.Google Scholar
[17]Call, G. S. and Silverman, J. H.. Canonical heights on varieties with morphisms. Compositio Math. 89(2) (1993), 163–205.Google Scholar
[18]Coman, D.. On the dynamics of a class of quadratic polynomial automorphisms of ℂ3. Discrete Contin. Dyn. Syst. 8(1) (2002), 55–67.Google Scholar
[19]Coman, D. and Fornæss, J. E.. Green’s functions for irregular quadratic polynomial automorphisms of C3. Michigan Math. J. 46(3) (1999), 419–459.Google Scholar
[20]Denis, L.. Points périodiques des automorphismes affines. J. Reine Angew. Math. 467 (1995), 157–167.Google Scholar
[21]Dikranjan, D., Goldsmith, B., Salce, L. and Zanardo, P.. Algebraic entropy for abelian groups. Trans. Amer. Math. Soc. 361(7) (2009), 3401–3434.Google Scholar
[22]Diller, J. and Favre, C.. Dynamics of bimeromorphic maps of surfaces. Amer. J. Math. 123(6) (2001), 1135–1169.Google Scholar
[23]Dinh, T.-C. and Sibony, N.. Une borne supérieure pour l’entropie topologique d’une application rationnelle. Ann. of Math. (2) 161(3) (2005), 1637–1644.Google Scholar
[24]Favre, C. and Jonsson, M.. Eigenvaluations. Ann. Sci. Éc. Norm. Supér. (4) 40(2) (2007), 309–349.Google Scholar
[25]Favre, C. and Jonsson, M.. Dynamical compactifications of C2. Ann. of Math. (2) 173(1) (2011), 211–248.Google Scholar
[26]Favre, C. and Wulcan, E.. Degree growth of monomial maps and McMullen’s polytope algebra. Indiana Math. J. to appear, 2010.Google Scholar
[27]Fornaess, J. E. and Sibony, N.. Complex dynamics in higher dimension. II. Modern Methods in Complex Analysis (Princeton, NJ, 1992) (Annals of Mathematics Studies, 137). Princeton University Press, Princeton, NJ, 1995, pp. 135–182.Google Scholar
[28]Ghioca, D. and Tucker, T. J.. Periodic points, linearizing maps, and the dynamical Mordell–Lang problem. J. Number Theory 129(6) (2009), 1392–1403.Google Scholar
[29]Ghioca, D., Tucker, T. J. and Zieve, M. E.. Intersections of polynomials orbits, and a dynamical Mordell–Lang conjecture. Invent. Math. 171(2) (2008), 463–483.Google Scholar
[30]Giordano Bruno, A. and Virili, S.. Algebraic Yuzvinski formula, 2011, arXiv:1111.1287.Google Scholar
[31]Grammaticos, B., Halburd, R. G., Ramani, A. and Viallet, C.-M.. How to detect the integrability of discrete systems. J. Phys. A 42(45) (2009), 454002, 30.Google Scholar
[32]Halburd, R. G.. Diophantine integrability. J. Phys. A 38(16) (2005), L263–L269.Google Scholar
[33]Hasselblatt, B. and Propp, J.. Degree-growth of monomial maps. Ergod. Th. & Dynam. Sys. 27(5) (2007), 1375–1397, Corrigendum 27(6) (2007), 1999.Google Scholar
[34]Hindry, M. and Silverman, J. H.. Diophantine Geometry: An Introduction (Graduate Texts in Mathematics, 201). Springer, New York, 2000.Google Scholar
[35]Hone, A. N. W.. Diophantine non-integrability of a third-order recurrence with the Laurent property. J. Phys. A 39(12) (2006), L171–L177.Google Scholar
[36]Jonsson, M. and Wulcan, E.. Stabilization of monomial maps. Michigan Math. J. 60 (2011), 629–660.Google Scholar
[37]Jonsson, M. and Wulcan, E.. Canonical heights for plane polynomial maps of small topological degree: a conjecture of Silverman. Preprint 2012, arXiv:1202.0203.Google Scholar
[38]Kawaguchi, S.. Canonical height functions for affine plane automorphisms. Math. Ann. 335(2) (2006), 285–310.Google Scholar
[39]Kawaguchi, S.. Local and global canonical height functions for affine space regular automorphisms. Preprint 2009, arXiv:0909.3573.Google Scholar
[40]Kawaguchi, S. and Silverman, J. H.. On the dynamical and arithmetic degrees of rational self-maps of algebraic varieties. Preprint 2012, arXiv:1208.0815.Google Scholar
[41]Lang, S.. Fundamentals of Diophantine Geometry. Springer, New York, 1983.Google Scholar
[42]Lee, C.. An upper bound for the height for regular affine automorphisms of 𝔸n. Math. Ann. to appear, 2009, arXiv:0909.3107.Google Scholar
[43]Lin, J.-L.. Pulling back cohomology classes and dynamical degrees of monomial maps. Bull. Soc. Math. France to appear, 2010, arXiv:1010.6285.Google Scholar
[44]Lin, J.-L.. Algebraic stability and degree growth of monomial maps. Math. Z. 271(1–2) (2012), 293–311.Google Scholar
[45]Maegawa, K.. Quadratic polynomial automorphisms of dynamical degree golden ratio of ℂ3. Ergod. Th. & Dynam. Sys. 21(3) (2001), 823–832.Google Scholar
[46]Marcello, S.. Sur la dynamique arithmétique des automorphismes de l’espace affine. Bull. Soc. Math. France 131(2) (2003), 229–257.Google Scholar
[47]Nguyên, V.-A.. Algebraic degrees for iterates of meromorphic self-maps of ℙk. Publ. Mat. 50(2) (2006), 457–473.Google Scholar
[48]Peters, J.. Entropy on discrete abelian groups. Adv. in Math. 33(1) (1979), 1–13.Google Scholar
[49]Peters, J.. Entropy of automorphisms on L.C.A. groups. Pacific J. Math. 96(2) (1981), 475–488.CrossRefGoogle Scholar
[50]Roberts, J. A. G. and Vivaldi, F.. Arithmetical method to detect integrability in maps. Phys. Rev. Lett. 90(3) (2003), 034102, 4.Google Scholar
[51]Roberts, J. A. G. and Vivaldi, F.. Signature of time-reversal symmetry in polynomial automorphisms over finite fields. Nonlinearity 18(5) (2005), 2171–2192.Google Scholar
[52]Roberts, J. A. G. and Vivaldi, F.. A combinatorial model for reversible rational maps over finite fields. Nonlinearity 22(8) (2009), 1965–1982.Google Scholar
[53]Russakovskii, A. and Shiffman, B.. Value distribution for sequences of rational mappings and complex dynamics. Indiana Univ. Math. J. 46(3) (1997), 897–932.Google Scholar
[54]Sibony, N.. Dynamique des applications rationnelles de ℙk. Dynamique et Géométrie Complexes (Lyon, 1997) (Panoramas et Synthèses, 8). Soc. Math. France, Paris, 1999, pp. ix–x, xi–xii, 97–185.Google Scholar
[55]Silverman, J. H.. Rational points on K3 surfaces: a new canonical height. Invent. Math. 105(2) (1991), 347–373.Google Scholar
[56]Silverman, J. H.. Geometric and arithmetic properties of the Hénon map. Math. Z. 215(2) (1994), 237–250.Google Scholar
[57]Silverman, J. H.. The Arithmetic of Dynamical Systems (Graduate Texts in Mathematics, 241). Springer, New York, 2007.Google Scholar
[58]Silverman, J. H.. The Arithmetic of Elliptic Curves, 2nd edn.(Graduate Texts in Mathematics, 106). Springer, Dordrecht, 2009.Google Scholar
[59]Truong, T. T.. Degree complexity of a family of birational maps. II. Exceptional cases. Math. Phys. Anal. Geom. 12(2) (2009), 157–180.Google Scholar
[60]Virili, S.. Entropy for endomorphisms of LCA groups. Topology Appl. 159(9) (2012), 2546–2556.Google Scholar
[61]Xie, J.. Periodic points of birational maps on the projective plane. Preprint 2011, arXiv:1106.1825.Google Scholar