Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T02:58:06.217Z Has data issue: false hasContentIssue false
  • English
  • Français

Dynamical Borel–Cantelli lemma for recurrence theory

Part of: Measure-theoretic ergodic theory Ergodic theory

Published online by Cambridge University Press:  12 April 2021

MUMTAZ HUSSAIN ,
BING LI ,
DAVID SIMMONS  and
BAOWEI WANG
MUMTAZ HUSSAIN
Affiliation:
La Trobe University, P.O. Box 199, Bendigo, VIC3552, Australia (e-mail: [email protected])
BING LI*
Affiliation:
School of Mathematics, South China University of Technology, Guangzhou510640, China
DAVID SIMMONS
Affiliation:
Department of Mathematics, University of York, Heslington, YorkYO10 5DD, UK (e-mail: [email protected])
BAOWEI WANG
Affiliation:
School of Mathematics and Statistics, Huazhong University of Science and Technology, 430074Wuhan, China (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

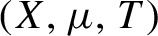We study the dynamical Borel–Cantelli lemma for recurrence sets in a measure-preserving dynamical system $(X, \mu , T)$ with a compatible metric d. We prove that under some regularity conditions, the 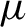$\mu $ -measure of the following set

$$\begin{align*}R(\psi)= \{x\in X : d(T^n x, x) < \psi(n)\ \text{for infinitely many}\ n\in\mathbb{N} \} \end{align*}$$
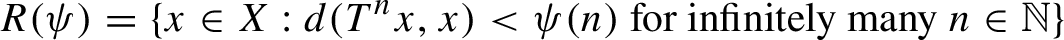
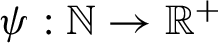obeys a zero–full law according to the convergence or divergence of a certain series, where $\psi :\mathbb {N}\to \mathbb {R}^+$ . The applications of our main theorem include the Gauss map, 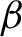$\beta $ -transformation and homogeneous self-similar sets.

Keywords

recurrencedynamical Borel-Cantelli lemmazero-full lawexponentially mixing

MSC classification

Primary: 37A05: Measure-preserving transformations
Secondary: 28D05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 6 , June 2022 , pp. 1994 - 2008
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, S. and Farmer, M.. Quantitative recurrence properties for self-conformal sets. Proc. Amer. Math. Soc. 149(3) (2021), 1127–1138.CrossRefGoogle Scholar
Barreira, L. and Saussol, B.. Hausdorff dimension of measures via Poincaré recurrence. Comm. Math. Phys. 219 (2001), 443–463.CrossRefGoogle Scholar
Boshernitzan, M. D.. Quantitative recurrence results. Invent. Math. 113(3) (1993), 617–631.CrossRefGoogle Scholar
Chang, Y., Wu, M. and Wu, W.. Quantitative recurrence properties and homogeneous self-similar sets. Proc. Amer. Math. Soc. 147(4) (2019), 1453–1465.CrossRefGoogle Scholar
Chernov, N. and Kleinbock, D.. Dynamical Borel–Cantelli lemmas for Gibbs measures. Israel J. Math. 122 (2001), 1–27.CrossRefGoogle Scholar
Kirsebom, M., Kunde, P. and Persson, T.. On shrinking targets and self-returning points. Preprint, 2020, arXiv:2003.01361v2.Google Scholar
Parry, W.. On the $\beta$ -expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Philipp, W.. Some metrical theorems in number theory. Pacific J. Math. 20 (1967), 109–127.CrossRefGoogle Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hungar. 8 (1957), 477–493.CrossRefGoogle Scholar
Schmeling, J.. Symbolic dynamics for $\beta$ -shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17(3) (1997), 675–694.CrossRefGoogle Scholar
Tan, B. and Wang, B.. Quantitative recurrence properties for beta-dynamical system. Adv. Math. 228(4) (2011), 2071–2097.CrossRefGoogle Scholar