Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T05:31:31.325Z Has data issue: false hasContentIssue false
  • English
  • Français

Dissipative conformal measures on locally compact spaces

Published online by Cambridge University Press:  10 November 2014

KLAUS THOMSEN
KLAUS THOMSEN*
Affiliation:
Institut for Matematik, Aarhus University, Ny Munkegade, 8000 Aarhus C, Denmark email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The paper introduces a general method to construct conformal measures for a local homeomorphism on a locally compact non-compact Hausdorff space, subject to mild irreducibility-like conditions. Among other things, the method is used to give necessary and sufficient conditions for the existence of eigenmeasures for the dual Ruelle operator associated to a locally compact non-compact irreducible Markov shift equipped with a uniformly continuous potential function. As an application to operator algebras the results are used to determine for which 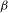${\it\beta}$ there are gauge invariant 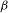${\it\beta}$-KMS weights on a simple graph 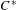$C^{\ast }$-algebra when the one-parameter automorphism group is given by a uniformly continuous real-valued function on the path space of the graph.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 649 - 670
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C.. Purely infinite C ∗ -algebras arising from dynamical systems. Bull. Soc. Math. France 125 (1997), 199–225.CrossRefGoogle Scholar
Cyr, V. T.. Transient Markov shifts. PhD Thesis, Pennsylvania State University, August 2010.Google Scholar
Deaconu, V.. Groupoids associated with endomorphisms. Trans. Amer. Math. Soc. 347 (1995), 1779–1786.CrossRefGoogle Scholar
Denker, M. and Urbanski, M.. On the existence of conformal measures. Trans. Amer. Math. Soc. 328 (1991), 563–587.CrossRefGoogle Scholar
Krengel, U.. Ergodic Theorems (de Gruyter Studies in Mathematics, 6). de Gruyter, Berlin, 1985.CrossRefGoogle Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J.. Graphs, groupoids, and Cuntz–Krieger algebras. J. Funct. Anal. 144 (1997), 505–541.CrossRefGoogle Scholar
Kumjian, A. and Renault, J.. KMS states on C ∗ -algebras associated to expansive maps. Proc. Amer. Math. Soc. 134 (2006), 2067–2078.CrossRefGoogle Scholar
Mayer, V. and Urbanski, M.. Geometric thermodynamic formalism and real analyticity for meromorphic functions of finite order. Ergod. Th. & Dynam. Sys. 28 (2008), 915–946.CrossRefGoogle Scholar
Mayer, V. and Urbanski, M.. Thermodynamic formalism and multifractal analysis for meromorphic functions of finite order. Mem. Amer. Math. Soc. 203(954) (2010).Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematical Studies, AM160). Princeton University Press, Princeton, NJ, 2006.Google Scholar
Renault, J.. A Groupoid Approach to C ∗ -algebras (Lecture Notes in Mathematics, 793). Springer, Berlin, 1980.CrossRefGoogle Scholar
Renault, J.. AF Equivalence Relations and their Cocycles Operator Algebras and Mathematical Physics (Constanţa, 2001). Theta Foundation, Bucharest, 2003, pp. 365–377.Google Scholar
Sarig, O.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19 (1999), 1565–1593.CrossRefGoogle Scholar
Sarig, O.. Lecture Notes on Thermodynamic Formalism for Toplogical Markov Shifts. Penn State University, 2009.Google Scholar
Sullivan, D.. Conformal dynamical systems. Geometric Analysis (Lecture Notes in Mathematics, 1007). Springer, Berlin, 1983, pp. 725–752.Google Scholar
Thomsen, K.. Semi-étale groupoids and applications. Ann. Inst. Fourier 60 (2010), 759–800.CrossRefGoogle Scholar
Thomsen, K.. On the C ∗ -algebra of a locally injective surjection and its KMS states. Comm. Math. Phys. 302 (2011), 403–423.CrossRefGoogle Scholar
Thomsen, K.. KMS states and conformal measures. Comm. Math. Phys. 316 (2012), 615–640.CrossRefGoogle Scholar
Thomsen, K.. KMS weights on groupoid and graph C ∗ -algebras. J. Funct. Anal. 266 (2014), 2959–2988.CrossRefGoogle Scholar
Thomsen, K.. On the positive eigenvalues and eigenvectors of a non-negative matrix. Preprint, June 2013; arXiv:1306.5116v1.Google Scholar
Walters, P.. Convergence of the Ruelle operator for a function satisfying Bowen’s condition. Trans. Amer. Math. Soc. 353 (2001), 327–347.CrossRefGoogle Scholar