Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:23:15.608Z Has data issue: false hasContentIssue false
  • English
  • Français

Dimension, recurrence via entropy and Lyapunov exponents for 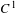$C^{1}$ map with singularities

Published online by Cambridge University Press:  19 September 2016

HONGWEI BAO
HONGWEI BAO*
Affiliation:
Yau Mathematical Sciences Center, Tsinghua University, Beijing 100084, China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 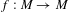$f:M\rightarrow M$ be a 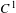$C^{1}$ self-map of a smooth Riemannian manifold 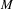$M$ and $\unicode[STIX]{x1D707}$ be an 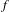$f$-invariant ergodic Borel probability measure with a compact support 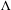$\unicode[STIX]{x1D6EC}$. We prove that if 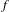$f$ is Hölder mild on the intersection of the singularity set and 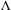$\unicode[STIX]{x1D6EC}$, then the pointwise dimension of $\unicode[STIX]{x1D707}$ can be controlled by the Lyapunov exponents of $\unicode[STIX]{x1D707}$ with respect to 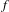$f$ and the entropy of 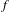$f$. Moreover, we establish the distinction of the Hausdorff dimension of the critical points sets of maps between the 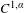$C^{1,\unicode[STIX]{x1D6FC}}$ continuity and Hölder mildness conditions. Consequently, this shows that the Hölder mildness condition is much weaker than the 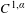$C^{1,\unicode[STIX]{x1D6FC}}$ continuity condition. As applications of our result, if we study the recurrence rate of 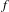$f$ instead of the pointwise dimension of $\unicode[STIX]{x1D707}$, then we deduce that the analogous relation exists between recurrence rate, entropy and Lyapunov exponents.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 3 , May 2018 , pp. 801 - 831
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L., Pesin, Y. and Schmeling, J.. Dimension and product structure of hyperbolic measures. Ann. of Math. (2) 149(3) (1999), 755–783.Google Scholar
Barreira, L. and Saussol, B.. Hausdorff dimension of measures via Poincaré recurrence. Comm. Math. Phys. 219(2) (2001), 443–463.Google Scholar
Barreira, L. and Wolf, C.. Pointwise dimension and ergodic decompositions. Ergod. Th. & Dynam. Sys. 26(3) (2006), 653–671.Google Scholar
Bonatti, C., Díaz, L. J. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity. A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102. Mathematical Physics, III) . Springer, Berlin, 2005.Google Scholar
Boshernitzan, M. D.. Quantitative recurrence results. Invent. Math. 113(3) (1993), 617–631.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, New York, 1975.Google Scholar
Brin, M. and Katok, A.. On local entropy. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007) . Springer, Berlin, 1983, pp. 30–38.Google Scholar
Cutler, C. D.. Connecting ergodicity and dimension in dynamical systems. Ergod. Th. & Dynam. Sys. 10(3) (1990), 451–462.Google Scholar
Eckmann, J.-P. and Ruelle, D.. Ergodic theory of chaos and strange attractors. Rev. Modern Phys. 57(3, part 1) (1985), 617–656.Google Scholar
Eckmann, J.-P. and Ruelle, D.. Addendum: ‘Ergodic theory of chaos and strange attractors’. Rev. Modern Phys. 57(4) (1985), 1115.Google Scholar
Falconer, K.. Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. John Wiley, Hoboken, NJ, 2003.Google Scholar
Farmer, J., Ott, E. and Yorke, J.. The dimension of chaotic attractors. Physica D 7(1–3) (1983), 153–180.Google Scholar
Federer, H.. Geometric Measure Theory (Die Grundlehren der mathematischen Wissenschaften, 153) . Springer, New York, 1969.Google Scholar
Huang, W. and Zhang, P.. Pointwise dimension, entropy and Lyapunov exponents for C 1 maps. Trans. Amer. Math. Soc. 364(12) (2012), 6355–6370.Google Scholar
Katok, A. and Strelcyn, J.-M.. Invariant Manifolds, Entropy and Billiards; Smooth Maps with Singularities (Lecture Notes in Mathematics, 1222) . Springer, Berlin, 1986.CrossRefGoogle Scholar
Kingman, J. F. C.. Subadditive Processes (Lecture Notes in Mathematics, 539) . Springer, Berlin, 1976.Google Scholar
Kobayashi, S. and Nomizu, K.. Foundations of Differential Geometry, Vol. I. Interscience/John Wiley, New York, 1963.Google Scholar
Kolmogorov, A. N.. A new metric invariant of transient dynamical systems and automorphisms in Lebesgue spaces. Dokl. Akad. Nauk SSSR (N.S.) 119 (1958), 861–864.Google Scholar
Ledrappier, F. and Misiurewicz, M.. Dimension of invariant measures for maps with exponent zero. Ergod. Th. & Dynam. Sys. 5(4) (1985), 595–610.CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. I. Characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122(3) (1985), 509–539.Google Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms. II. Relations between entropy, exponents and dimension. Ann. of Math. (2) 122(3) (1985), 540–574.Google Scholar
Lee, J. M.. Introduction to Smooth Manifolds (Graduate Texts in Mathematics, 218) . 2nd edn. Springer, New York, 2013.Google Scholar
Mañé, R.. A proof of Pesin’s formula. Ergod. Th. & Dynam. Sys. 1(1) (1981), 95–102.Google Scholar
Mañé, R.. The Hausdorff dimension of invariant probabilities of rational maps. Dynamical Systems, Valparaiso 1986 (Lecture Notes in Mathematics, 1331) . Springer, Berlin, 1988, pp. 86–117.Google Scholar
Manning, A.. The dimension of the maximal measure for a polynomial map. Ann. of Math. (2) 119(2) (1984), 425–430.Google Scholar
Mattila, P.. Geometry of Sets and Measures in Euclidean Spaces. Fractals and Rectifiability (Cambridge Studies in Advanced Mathematics, 44) . Cambridge University Press, Cambridge, 1995.Google Scholar
Oseledets, V. I.. A multiplicative ergodic theorem. Characteristic Ljapunov, exponents of dynamical systems. Tr. Mosk. Mat. Obs. 19 (1968), 179–210 (in Russian); Engl. transl. Trans. Moscow Math. Soc. 19 (1968), 197–221.Google Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems. Contemporary Views and Applications (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, IL, 1997.Google Scholar
Pesin, Y. and Weiss, H.. On the dimension of deterministic and random Cantor-like sets, symbolic dynamics, and the Eckmann–Ruelle conjecture. Comm. Math. Phys. 182(1) (1996),105C153.Google Scholar
Sinaĭ, Y.. On the concept of entropy for a dynamic system. Dokl. Akad. Nauk SSSR 124 (1959), 768–771.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.Google Scholar
Young, L.-S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2(1) (1982), 109–124.Google Scholar
Young, L.-S.. Ergodic theory of attractors. Proceedings of the International Congress of Mathematicians, Vols. 1, 2 (Zürich, 1994). Birkhäuser, Basel, 1995, pp. 1230–1237.Google Scholar
Young, L.-S.. Ergodic theory of differentiable dynamical systems. Real and Complex Dynamical Systems. Eds. Branner, B. and Hjorth, P.. Kluwer Academic, Dordrecht, 1995, pp. 293–336.Google Scholar