No CrossRef data available.
Article contents
Dimension estimates and approximation in non-uniformly hyperbolic systems
Published online by Cambridge University Press: 12 February 2024
Abstract
Let 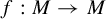 $f: M\rightarrow M$ be a
$f: M\rightarrow M$ be a 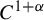 $C^{1+\alpha }$ diffeomorphism on an
$C^{1+\alpha }$ diffeomorphism on an 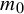 $m_0$-dimensional compact smooth Riemannian manifold M and
$m_0$-dimensional compact smooth Riemannian manifold M and 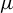 $\mu $ a hyperbolic ergodic f-invariant probability measure. This paper obtains an upper bound for the stable (unstable) pointwise dimension of
$\mu $ a hyperbolic ergodic f-invariant probability measure. This paper obtains an upper bound for the stable (unstable) pointwise dimension of 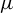 $\mu $, which is given by the unique solution of an equation involving the sub-additive measure-theoretic pressure. If
$\mu $, which is given by the unique solution of an equation involving the sub-additive measure-theoretic pressure. If 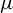 $\mu $ is a Sinai–Ruelle–Bowen (SRB) measure, then the Kaplan–Yorke conjecture is true under some additional conditions and the Lyapunov dimension of
$\mu $ is a Sinai–Ruelle–Bowen (SRB) measure, then the Kaplan–Yorke conjecture is true under some additional conditions and the Lyapunov dimension of 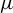 $\mu $ can be approximated gradually by the Hausdorff dimension of a sequence of hyperbolic sets
$\mu $ can be approximated gradually by the Hausdorff dimension of a sequence of hyperbolic sets 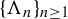 $\{\Lambda _n\}_{n\geq 1}$. The limit behaviour of the Carathéodory singular dimension of
$\{\Lambda _n\}_{n\geq 1}$. The limit behaviour of the Carathéodory singular dimension of 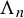 $\Lambda _n$ on the unstable manifold with respect to the super-additive singular valued potential is also studied.
$\Lambda _n$ on the unstable manifold with respect to the super-additive singular valued potential is also studied.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



