Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-28T11:03:25.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Difference sets and frequently hypercyclic weighted shifts

Published online by Cambridge University Press:  13 November 2013

FRÉDÉRIC BAYART  and
IMRE Z. RUZSA
FRÉDÉRIC BAYART
Affiliation:
Clermont Université, Université Blaise Pascal, Laboratoire de Mathematiques, BP 10448, F-63000 Clermont-Ferrand, France email [email protected] CNRS, UMR 6620, Laboratoire de Mathématiques, F-63177 Aubiere, France email [email protected]
IMRE Z. RUZSA
Affiliation:
Alfréd Rényi Institute of Mathematics, Pf. 127, H-1364 Budapest, Hungary email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

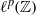We solve several problems on frequently hypercyclic operators. Firstly, we characterize frequently hypercyclic weighted shifts on ${\ell }^{p} ( \mathbb{Z} )$, 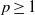$p\geq 1$. Our method uses properties of the difference set of a set with positive upper density. Secondly, we show that there exists an operator which is 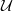$ \mathcal{U} $-frequently hypercyclic but not frequently hypercyclic, and that there exists an operator which is frequently hypercyclic but not distributionally chaotic. These (surprising) counterexamples are given by weighted shifts on 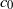${c}_{0} $. The construction of these shifts lies on the construction of sets of positive integers whose difference sets have very specific properties.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 3 , May 2015 , pp. 691 - 709
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayart, F. and Grivaux, S.. Hypercyclicity and unimodular point spectrum. J. Funct. Anal. 226 (2005), 281–300.CrossRefGoogle Scholar
Bayart, F. and Grivaux, S.. Frequently hypercyclic operators. Trans. Amer. Math. Soc. 358 (2006), 5083–5117.CrossRefGoogle Scholar
Bayart, F. and Grivaux, S.. Invariant Gaussian measures for operators on Banach spaces and linear dynamics. Proc. Lond. Math. Soc. 94 (2007), 181–210.Google Scholar
Bayart, F. and Matheron, É.. Dynamics of Linear Operators (Cambridge Tracts in Mathematics, 179). Cambridge University Press, Cambridge, 2009.Google Scholar
Bayart, F. and Matheron, É.. Mixing operators and small subsets of the circle. Preprint, 2011, arXiv:1112.1289.Google Scholar
Bergelson, V.. Ergodic Ramsey theory: an update. Ergodic Theory of ℤd Actions (Warwick, 1993–1994) (London Mathematical Society Lecture Note Series, 228). Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bernardes, N. C., Bonnila, A., Müller, V. and Peris, A.. Distributional chaos for linear operators. Preprint, 2013.Google Scholar
Bonilla, A. and Grosse-Erdmann, K.-G.. Frequently hypercyclic operators and vectors. Ergod. Th. & Dynam. Sys. 27 (2007), 383–404.CrossRefGoogle Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Grivaux, S.. A new class of frequently hypercyclic operators. Indiana Univ. Math. J. 60 (2011), 1177–1201.Google Scholar
Grosse-Erdmann, K.-G. and Peris, A.. Frequently dense orbits. C. R. Acad. Sci. Paris 341 (2005), 123–128.Google Scholar
Grosse-Erdmann, K.-G. and Peris, A.. Linear Chaos (Universitext). Springer, London, 2011.Google Scholar
Ruzsa, I.. On difference-sequences. Acta Arith. 25 (1973/74), 151–157.Google Scholar
Salas, H. N.. Hypercyclic weighted shifts. Trans. Amer. Math. Soc. 347 (3) (1995), 993–1004.Google Scholar
Schweizer, B. and Smítal, J.. Measures of chaos and a spectral decomposition of dynamical systems on the interval. Trans. Amer. Math. Soc. 344 (2) (1994), 737–754.CrossRefGoogle Scholar
Shkarin, S.. On the spectrum of frequently hypercyclic operators. Proc. Amer. Math. Soc. 137 (2009), 123–134.CrossRefGoogle Scholar