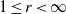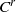Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Buzzi, Jérôme
and
Fisher, Todd
2013.
Entropic stability beyond partial hyperbolicity.
Journal of Modern Dynamics,
Vol. 7,
Issue. 4,
p.
527.
Burguet, David
Liao, Gang
and
Yang, Jiagang
2015.
Asymptotich-expansiveness rate ofC∞maps.
Proceedings of the London Mathematical Society,
Vol. 111,
Issue. 2,
p.
381.
Buzzi, Jérôme
Crovisier, Sylvain
and
Fisher, Todd
2018.
The entropy of 𝐶¹-diffeomorphisms without a dominated splitting.
Transactions of the American Mathematical Society,
Vol. 370,
Issue. 9,
p.
6685.
HU, HUYI
WU, WEISHENG
and
ZHU, YUJUN
2021.
Unstable pressure and u-equilibrium states for partially hyperbolic diffeomorphisms.
Ergodic Theory and Dynamical Systems,
Vol. 41,
Issue. 11,
p.
3336.
Tahzibi, Ali
2021.
Unstable entropy in smooth ergodic theory
*
.
Nonlinearity,
Vol. 34,
Issue. 8,
p.
R75.
Rocha, Joas Elias
and
Tahzibi, Ali
2022.
On the number of ergodic measures of maximal entropy for partially hyperbolic diffeomorphisms with compact center leaves.
Mathematische Zeitschrift,
Vol. 301,
Issue. 1,
p.
471.
Yang, Dawei
and
Zhang, Jinhua
2022.
Ergodic optimization for some dynamical systems beyond uniform hyperbolicity.
Dynamical Systems,
Vol. 37,
Issue. 4,
p.
630.
Biś, Andrzej
Carvalho, Maria
Mendes, Miguel
and
Varandas, Paulo
2022.
A Convex Analysis Approach to Entropy Functions, Variational Principles and Equilibrium States.
Communications in Mathematical Physics,
Vol. 394,
Issue. 1,
p.
215.
Buzzi, Jérôme
Crovisier, Sylvain
and
Sarig, Omri
2022.
Continuity properties of Lyapunov exponents for surface diffeomorphisms.
Inventiones mathematicae,
Vol. 230,
Issue. 2,
p.
767.
Buzzi, Jérôme
2023.
Entropie et classification en dynamique.
Séminaire Laurent Schwartz — EDP et applications,
p.
1.
Burguet, David
2024.
Maximal Measure and Entropic Continuity of Lyapunov Exponents for $${\mathcal {C}}^r$$ Surface Diffeomorphisms with Large Entropy.
Annales Henri Poincaré,
Vol. 25,
Issue. 2,
p.
1485.