Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T04:21:15.449Z Has data issue: false hasContentIssue false
  • English
  • Français

A convex structure on sofic embeddings

Published online by Cambridge University Press:  14 March 2013

LIVIU PĂUNESCU
LIVIU PĂUNESCU*
Affiliation:
University of Vienna, Nordbergstrasse 15, 1090 Wien, Austria Institute of Mathematics ‘Simion Stoilow’, 21 Calea Grivitei Street, Bucharest, 010702, Romania email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Nathanial Brown [Topological dynamical systems associated to 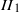${\mathit{II}}_{1} $-factors. Adv. Math. 227(4), 1665–1699] introduced a convex-like structure on the set of unitary equivalence classes of unital *-homomorphisms of a separable type 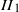${\mathit{II}}_{1} $ factor into 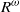${R}^{\omega } $ (ultrapower of the hyperfinite factor). The goal of this paper is to introduce such a structure on the set of sofic representations of groups. We prove that if the commutant of a representation acts ergodically on the Loeb measure space then that representation is an extreme point.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1343 - 1352
Copyright
Copyright ©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brown, N.. Topological dynamical systems associated to ${\mathit{II}}_{1} $-factors. Adv. Math. 227(4), 1665–1699.Google Scholar
Capraro, V. and Fritz, T.. On the axiomatization of convex subsets of Banach spaces. Proc. Amer. Math. Soc. to appear. Published online 2 January 2013, http://dx.doi.org/10.1090/S0002-9939-2013-11465-6.Google Scholar
Capraro, V. and Păunescu, L.. Product between ultrafilters and applications to the Connes’ embedding problem. J. Operator Theory 68(1), 165–172.Google Scholar
Cornulier, Y.. A sofic group away from amenable groups. Math. Ann. 350 (2) (2011), 269–275.Google Scholar
Elek, G. and Szabo, E.. Hyperlinearity, essentially free actions and L2-invariants. The sofic property. Math. Ann. 332 (2) (2005), 421–441.Google Scholar
Elek, G. and Szabo, E.. Sofic representations of amenable groups. Proc. Amer. Math. Soc. 139 (2011), 4285–4291.Google Scholar
Elek, G. and Szegedy, B.. Limits of hypergaphs, removal and regularity lemmas. A non-standard approach. Preprint, arXiv: 0705.2179v1.Google Scholar
Gromov, M.. Endomorphism of symbolic algebraic varieties. J. Eur. Math. Soc. 1 (1999), 109–197.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Combinatorial independence and sofic entropy. Preprint, arXiv: 1208.2464. Comm. Math. Stat. to appear.Google Scholar
Loeb, P. E.. Conversion from nonstandard to standard measure spaces and applications in probability theory. Trans. Amer. Math. Soc. 211 (1975), 113–122.Google Scholar
Păunescu, L.. On sofic actions and equivalence relations. J. Funct. Anal. 261 (9) (2011), 2461–2485.Google Scholar
Pestov, V.. Hyperlinear and sofic groups: a brief guide. Bull. Symbolic Logic 14 (4) (2008), 449–480.Google Scholar
Pestov, V. and Kwiatkowska, A.. An introduction to hyperlinear and sofic groups. Preprint, 2009, arXiv: 0911.4266.Google Scholar
Popa, S.. On a problem of R. V. Kadison on maximal abelian *-subalgebras in factors. Invent. Math. 65 (1981), 269–281.Google Scholar