Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-30T20:05:29.086Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuous orbit equivalence rigidity

Published online by Cambridge University Press:  08 November 2016

XIN LI
XIN LI*
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, Mile End Road, London E1 4NS, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

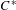We take the first steps towards a better understanding of continuous orbit equivalence, i.e., topological orbit equivalence with continuous cocycles. First, we characterize continuous orbit equivalence in terms of isomorphisms of $C^{\ast }$-crossed products preserving Cartan subalgebras. This is the topological analogue of the classical result by Singer and Feldman-Moore in the measurable setting. Second, we turn to continuous orbit equivalence rigidity, i.e., the question whether for certain classes of topological dynamical systems, continuous orbit equivalence implies conjugacy. We show that this is not always the case by constructing topological dynamical systems (actions of free abelian groups and also non-abelian free groups) that are continuously orbit equivalent but not conjugate. Furthermore, we prove positive rigidity results. For instance, for solvable duality groups, general topological Bernoulli actions and certain subshifts of full shifts over finite alphabets are rigid.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1543 - 1563
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barlak, S. and Li, X.. Cartan subalgebras and the UCT problem. Preprint, 2015, arXiv:1511.02697v2.Google Scholar
Boyle, M. and Tomiyama, J.. Bounded topological orbit equivalence and C ∗ -algebras. J. Math. Soc. Japan 50 (1998), 317–329.CrossRefGoogle Scholar
Brown, K. S.. Cohomology of Groups (Graduate Texts in Mathematics, 87) . Springer, New York, 1982.CrossRefGoogle Scholar
Burton, R. and Steif, J. E.. Some 2-D symbolic dynamical systems: entropy and mixing. Ergodic Theory of ℤ d -Actions (LMS Lecture Notes Series, 228) . Eds. Pollicott, M. and Schmidt, K.. Cambridge University Press, Cambridge, 1996, pp. 297–305.Google Scholar
Chung, N.-P. and Jiang, Y.. Continuous cocycle superrigidity for shifts and groups with one end. Preprint, 2016, arXiv:1603.00114.CrossRefGoogle Scholar
Cuntz, J., Echterhoff, S. and Li, X.. On the K-theory of crossed products by automorphic semigroup actions. Q. J. Math. 64 (2013), 747–784.Google Scholar
de la Harpe, P.. Topics in Geometric Group Theory (Chicago Lectures in Mathematics) . University of Chicago Press, Chicago, 2000.Google Scholar
Feldman, J. and Moore, C.. Ergodic equivalence relations, cohomology, and von Neumann algebras. I. Trans. Amer. Math. Soc. 234 (1977), 289–324.Google Scholar
Feldman, J. and Moore, C.. Ergodic equivalence relations, cohomology, and von Neumann algebras. II. Trans. Amer. Math. Soc. 234 (1977), 325–359.Google Scholar
Furman, A.. Orbit equivalence rigidity. Ann. of Math. (2) 150 (1999), 1083–1108.CrossRefGoogle Scholar
Gaboriau, D.. Orbit equivalence and measured group theory. Proceedings of the ICM (Hyderabad, India, 2010), Vol. III. Hindustan Book Agency, Hyderabad, India, 2010, pp. 1501–1527.Google Scholar
Giordano, T., Matui, H., Putnam, I. F. and Skau, C. F.. Orbit equivalence for Cantor minimal ℤ2 -systems. J. Amer. Math. Soc. 21 (2008), 863–892.CrossRefGoogle Scholar
Giordano, T., Matui, H., Putnam, I. F. and Skau, C. F.. Orbit equivalence for Cantor minimal ℤ d -systems. Invent. Math. 179 (2010), 119–158.CrossRefGoogle Scholar
Giordano, T., Putnam, I. F. and Skau, C. F.. Topological orbit equivalence and C ∗ -crossed products. J. Reine Angew. Math. 469 (1995), 51–111.Google Scholar
Ioana, A.. W ∗ -superrigidity for Bernoulli actions of property (T) groups. J. Amer. Math. Soc. 24 (2011), 1175–1226.CrossRefGoogle Scholar
Kida, Y.. Measure equivalence rigidity of the mapping class group. Ann. of Math. (2) 171 (2010), 1851–1901.Google Scholar
Li, X.. Partial transformation groupoids attached to graphs and semigroups. Int. Math. Res. Not. IMRN to appear, Preprint, 2016, arXiv:1603.09165.CrossRefGoogle Scholar
Li, X.. Quasi-isometry, Kakutani equivalence and applications to cohomology. Preprint, 2016, arXiv:1604.07375.Google Scholar
Matsumoto, K. and Matui, H.. Continuous orbit equivalence of topological Markov shifts and Cuntz–Krieger algebras. Kyoto J. Math. 54 (2014), 863–877.CrossRefGoogle Scholar
Medynets, K., Sauer, R. and Thom, A.. Cantor systems and quasi-isometry of groups. Preprint, 2015,arXiv:1508.07578.Google Scholar
Monod, N. and Shalom, Y.. Orbit equivalence rigidity and bounded cohomology. Ann. of Math. (2) 164 (2006), 825–878.CrossRefGoogle Scholar
Popa, S.. Cocycle and orbit equivalence superrigidity for malleable actions of w-rigid groups. Invent. Math. 170 (2007), 243–295.Google Scholar
Popa, S.. On the superrigidity of malleable actions with spectral gap. J. Amer. Math. Soc. 21 (2008), 981–1000.CrossRefGoogle Scholar
Renault, J.. Cartan subalgebras in C ∗ -algebras. Irish Math. Soc. Bull. 61 (2008), 29–63.CrossRefGoogle Scholar
Schmidt, K.. The cohomology of higher-dimensional shifts of finite type. Pacific J. Math. 170 (1995), 237–270.Google Scholar
Schmidt, K.. Tilings, fundamental cocycles and fundamental groups of symbolic ℤ d -actions. Ergod. Th. & Dynam. Sys. 18 (1998), 1473–1525.CrossRefGoogle Scholar
Serre, J.P.. Local Fields. Springer, Berlin, 1979.Google Scholar
Serre, J.P.. Galois Cohomology. Springer, Berlin, 1997.CrossRefGoogle Scholar
Singer, I.M.. Automorphisms of finite factors. Amer. J. Math. 77 (1955), 117–133.Google Scholar
Suzuki, Y.. Amenable minimal Cantor systems of free groups arising from diagonal actions. J. Reine Angew. Math. to appear, Preprint, 2013, arXiv:1312.7098v4.Google Scholar
Vaes, S.. Rigidity results for Bernoulli actions and their von Neumann algebras (after Sorin Popa). Astérisque 311 (2007), 237–294.Google Scholar
Vaes, S.. Rigidity for von Neumann algebras and their invariants. Proceedings of the ICM (Hyderabad, India, 2010), Vol. III. Hindustan Book Agency, Hyderabad, India, 2010, pp. 1624–1650.Google Scholar
Zimmer, R. J.. Ergodic Theory and Semisimple Groups (Monographs in Mathematics, 81) . Birkhäuser, Basel, 1984.Google Scholar