Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T04:49:47.395Z Has data issue: false hasContentIssue false
  • English
  • Français

Constant slope, entropy, and horseshoes for a map on a tame graph

Part of: Topological dynamics Low-dimensional dynamical systems

Published online by Cambridge University Press:  22 April 2019

ADAM BARTOŠ Open the ORCID record for ADAM BARTOŠ [Opens in a new window] ,
JOZEF BOBOK Open the ORCID record for JOZEF BOBOK [Opens in a new window] ,
PAVEL PYRIH Open the ORCID record for PAVEL PYRIH [Opens in a new window] ,
SAMUEL ROTH Open the ORCID record for SAMUEL ROTH [Opens in a new window]  and
BENJAMIN VEJNAR Open the ORCID record for BENJAMIN VEJNAR [Opens in a new window]
ADAM BARTOŠ
Affiliation:
Charles University in Prague, Faculty of Mathematics and Physics, Department of Mathematical Analysis, Czech Republic email [email protected], [email protected], [email protected]
JOZEF BOBOK
Affiliation:
Czech Technical University in Prague, Faculty of Civil Engineering, Czech Republic email [email protected]
PAVEL PYRIH
Affiliation:
Charles University in Prague, Faculty of Mathematics and Physics, Department of Mathematical Analysis, Czech Republic email [email protected], [email protected], [email protected]
SAMUEL ROTH
Affiliation:
Silesian University in Opava, Mathematical Institute, Czech Republic email [email protected]
BENJAMIN VEJNAR
Affiliation:
Charles University in Prague, Faculty of Mathematics and Physics, Department of Mathematical Analysis, Czech Republic email [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study continuous countably (strictly) monotone maps defined on a tame graph, i.e. a special Peano continuum for which the set containing branch points and end points has countable closure. In our investigation we confine ourselves to the countable Markov case. We show a necessary and sufficient condition under which a locally eventually onto, countably Markov map 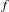$f$ of a tame graph 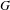$G$ is conjugate to a map $g$ of constant slope. In particular, we show that in the case of a Markov map 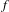$f$ that corresponds to a recurrent transition matrix, the condition is satisfied for a constant slope $e^{h_{\text{top}}(f)}$, where 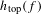$h_{\text{top}}(f)$ is the topological entropy of 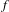$f$. Moreover, we show that in our class the topological entropy 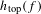$h_{\text{top}}(f)$ is achievable through horseshoes of the map 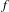$f$.

Keywords

Markov maptame graphconstant slopeconjugacyentropy

MSC classification

Primary: 37E25: Maps of trees and graphs
Secondary: 37B40: Topological entropy 37B45: Continua theory in dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 11 , November 2020 , pp. 2970 - 2994
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsedà, L., Llibre, J. and Misiurewicz, M.. Combinatorial Dynamics and Entropy in Dimension One (Advanced Series in Nonlinear Dynamics, 5) , 2nd edn. World Scientific, Singapore, 2000.10.1142/4205CrossRefGoogle Scholar
Alsedà, L. and Misiurewicz, M.. Semiconjugacy to a map of a constant slope. Discrete Contin. Dyn. Syst. Ser. B 20 (2015), 3403–3413.Google Scholar
Baillif, M. and de Carvalho, A.. Piecewise linear model for tree maps. Internat. J. Bifur. Chaos Appl. Sci. Engrg. 11(12) (2001), 3163–3169.CrossRefGoogle Scholar
Bobok, J. and Bruin, H.. Constant slope maps and the Vere-Jones classification. Entropy 18(6) (2016), paper No. 234, 27 pp.10.3390/e18060234CrossRefGoogle Scholar
Bobok, J. and Roth, S.. The infimum of Lipschitz constants in the conjugacy class of an interval map. Proc. Amer. Math. Soc. 147(1) (2019), 255–269.10.1090/proc/14255CrossRefGoogle Scholar
Dai, X., Zhou, Z. and Geng, X.. Some relations between Hausdorff-dimensions and entropies. Sci. China Ser. A 41 (1998), 1068–1075.CrossRefGoogle Scholar
Gurevič, B. M.. Topological entropy for denumerable Markov chains. Dokl. Akad. Nauk SSSR 10 (1969), 911–915.Google Scholar
Hofbauer, F.. On intrinsic ergodicity of piecewise monotonic transformations with positive entropy. Israel J. Math. 34(3) (1979), 213–237.CrossRefGoogle Scholar
Kitchens, B. P.. Symbolic Dynamics: One-sided, Two-sided, and Countable State Markov Shifts (Universitext) . Springer, New York, 1998.CrossRefGoogle Scholar
Milnor, J. and Thurston, W.. On iterated maps of the interval. Dynamical Systems (Lecture Notes in Mathematics, 1342) . Springer, Berlin, 1988, pp. 465–563.10.1007/BFb0082847CrossRefGoogle Scholar
Misiurewicz, M.. Horseshoes for mappings of an interval. Bull. Acad. Pol. Sci. Sér. Sci. Math. 27 (1979), 167–169.Google Scholar
Misiurewicz, M.. On Bowen’s definition of topological entropy. Discrete Contin. Dyn. Syst. Ser. A 10 (2004), 827–833.10.3934/dcds.2004.10.827CrossRefGoogle Scholar
Misiurewicz, M. and Roth, S.. Constant slope maps on the extended real line. Ergod. Th. & Dynam. Sys. 38 (2018), 3145–3169.CrossRefGoogle Scholar
Nadler, S. B.. Continuum Theory: An Introduction. Marcel Dekker, New York, 1992.CrossRefGoogle Scholar
Parry, W.. Symbolic dynamics and transformations of the unit interval. Trans. Amer. Math. Soc. 122 (1966), 368–378.CrossRefGoogle Scholar
Pruitt, W.. Eigenvalues of non-negative matrices. Ann. Math. Statist. 35(4) (1964), 1797–1800.10.1214/aoms/1177700401CrossRefGoogle Scholar
Vere-Jones, D.. Geometric ergodicity in denumerable Markov chains. Q. J. Math. Oxford Ser. 13 (1962), 7–28.CrossRefGoogle Scholar
Vere-Jones, D.. Ergodic properties of nonnegative matrices I. Pacific J. Math. 22 (1967), 361–386.10.2140/pjm.1967.22.361CrossRefGoogle Scholar