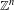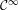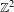Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Eynard-Bontemps, Hélène
2016.
On the connectedness of the space of codimension one foliations on a closed 3-manifold.
Inventiones mathematicae,
Vol. 204,
Issue. 2,
p.
605.
Eynard-Bontemps, Hélène
and
Navas, Andrés
2021.
Mather invariant, distortion, and conjugates for diffeomorphisms of the interval.
Journal of Functional Analysis,
Vol. 281,
Issue. 9,
p.
109149.