Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T21:24:03.087Z Has data issue: false hasContentIssue false
  • English
  • Français

A condition that implies full homotopical complexity of orbits for surface homeomorphisms

Part of: Low-dimensional dynamical systems Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  24 September 2019

SALVADOR ADDAS-ZANATA  and
BRUNO DE PAULA JACOIA
SALVADOR ADDAS-ZANATA
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Brazil email [email protected]
BRUNO DE PAULA JACOIA
Affiliation:
Rua do Matão 1010, Cidade Universitária, 05508-090São Paulo, SP, Brazil email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

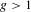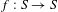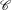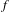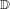We consider closed orientable surfaces $S$ of genus $g>1$ and homeomorphisms $f:S\rightarrow S$ isotopic to the identity. A set of hypotheses is presented, called a fully essential system of curves $\mathscr{C}$ and it is shown that under these hypotheses, the natural lift of $f$ to the universal cover of $S$ (the Poincaré disk $\mathbb{D}$), denoted by 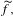$\widetilde{f},$ has complicated and rich dynamics. In this context, we generalize results that hold for homeomorphisms of the torus isotopic to the identity when their rotation sets contain zero in the interior. In particular, for 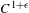$C^{1+\unicode[STIX]{x1D716}}$ diffeomorphisms, we show the existence of rotational horseshoes having non-trivial displacements in every homotopical direction. As a consequence, we found that the homological rotation set of such an 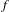$f$ is a compact convex subset of 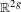$\mathbb{R}^{2g}$ with maximal dimension and all points in its interior are realized by compact 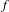$f$-invariant sets and by periodic orbits in the rational case. Also, 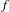$f$ has uniformly bounded displacement with respect to rotation vectors in the boundary of the rotation set. This implies, in case where 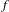$f$ is area preserving, that the rotation vector of Lebesgue measure belongs to the interior of the rotation set.

Keywords

low dimensional dynamicstopological dynamicsrotation setsrotational horseshoespseudo-Anosov maps

MSC classification

Primary: 37E30: Homeomorphisms and diffeomorphisms of planes and surfaces 37E45: Rotation numbers and vectors
Secondary: 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.) 37C25: Fixed points, periodic points, fixed-point index theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 1 , January 2021 , pp. 1 - 47
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Addas-Zanata, S.. Area preserving diffeomorphisms of the torus whose rotation sets have non empty interiors. Ergod. Th. & Dynam. Sys. 1 (2015), 1–33.Google Scholar
Addas-Zanata, S.. Uniform bounds for diffeomorphisms of the torus and a conjecture of Boyland. J. Lond. Math. Soc. (2) 91 (2015), 537–553.Google Scholar
Boyland, P.. Isotopy stability of dynamics on surfaces. Contemp. Math. 246 (1999), 17–45.Google Scholar
Boyland, P.. Transitivity of surface dynamics lifted to Abelian covers. Ergod. Th. & Dynam. Sys. 29 (2009), 1417–1449.Google Scholar
Brown, M.. A new proof of Brouwer’s lemma on translation arcs. Houston J. Math. 10 (1984), 35–41.Google Scholar
Burns, K. and Weiss, H.. A geometric criterion for positive topological entropy. Comm. Math. Phys. 172 (1995), 95–118.Google Scholar
De Carvalho, A. and Paternain, M.. Monotone quotients of surface diffeomorphisms. Math. Res. Lett. 10 (2003), 603–619.10.4310/MRL.2003.v10.n5.a4Google Scholar
Farb, B. and Margalit, D.. A Primer on Mapping Class Groups. Princeton University Press, Princeton, NJ, 2011.10.1515/9781400839049Google Scholar
Fathi, A., Laudenbach, F. and Poenaru, V.. Travaux de Thurston sur les surfaces. Astérisque 66–67 (1979).Google Scholar
Franks, J.. Realizing rotation vectors for torus homeomorphisms. Trans. Amer. Math. Soc. 311 (1989), 107–115.10.1090/S0002-9947-1989-0958891-1Google Scholar
Franks, J.. Rotation vectors and fixed points of area preserving surface diffeomorphisms. Trans. Amer. Math. Soc. 348 (1996), 2637–2662.Google Scholar
Gromov, M.. Metric Structures for Riemannian and Non-Riemannian Spaces. Birkhauser, Basel, 2007.Google Scholar
Guelman, N., Koropecki, A. and Tal, F.. Rotation sets with nonempty interior and transitivity in the universal covering. Ergod. Th. & Dynam. Sys. 35 (2015), 883–894.Google Scholar
Handel, M.. Global shadowing of pseudo-Anosov homeomorphisms. Ergod. Th. & Dynam. Sys. 5 (1985), 373–377.Google Scholar
Handel, M.. The rotation set of a homeomorphism of the annulus is closed. Comm. Math. Phys. 17 (1990), 339–349.Google Scholar
Handel, M.. A fixed-point theorem for planar homeomorphisms. Topology 38 (1990), 235–264.Google Scholar
Hadwinger, H., Debrunner, H. and Klee, V.. Combinatorial Geometry in the Plane. Holt, Rinehart and Winston, New York, NY, 1964.Google Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.10.1007/BF02684777Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Koropecki, A. and Tal, F.. Strictly toral dynamics. Invent. Math. 196 (2015), 339–381.10.1007/s00222-013-0470-3Google Scholar
Koropecki, A. and Tal, F.. Fully essential dynamics for area-preserving surface homeomorphisms. Ergod. Th. & Dynam. Sys. 38(5) (2017), 1791–1836.Google Scholar
Le Calvez, P.. Une nouvelle preuve du théoréme de point fixe de Handel. Geom. Topol. 10 (2006), 2299–2349.Google Scholar
Llibre, J. and Mackay, R.. Rotation vectors and entropy for homeomorphisms of the torus isotopic to the identity. Ergod. Th. & Dynam. Sys. 11 (1991), 115–128.Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets for maps of tori. J. Lond. Math. Soc. (2) 40 (1989), 490–506.10.1112/jlms/s2-40.3.490Google Scholar
Misiurewicz, M. and Ziemian, K.. Rotation sets and ergodic measures for torus homeomorphisms. Fund. Math. 137 (1990), 45–52.10.4064/fm-137-1-45-52Google Scholar
Palis, J.. On Morse–Smale dynamical systems. Topology 8 (1968), 385–404.10.1016/0040-9383(69)90024-XGoogle Scholar
Passeggi, A.. Personal communication, 2018.Google Scholar
Schwartzman, S.. Asymptotic cycles. Ann. of Math. (2) 66 (1957), 270–284.Google Scholar