Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T20:39:37.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing dynamical degrees of rational maps on moduli space

Published online by Cambridge University Press:  21 July 2015

SARAH KOCH  and
ROLAND K. W. ROEDER
SARAH KOCH
Affiliation:
University of Michigan, East Hall, 530 Church Street, Ann Arbor, MI 48109, USA email [email protected]
ROLAND K. W. ROEDER
Affiliation:
IUPUI, Department of Mathematical Sciences, LD Building, Room 270, 402 North Blackford Street, Indianapolis, IN 46202-3267, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamical degrees of a rational map 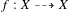$f:X{\dashrightarrow}X$ are fundamental invariants describing the rate of growth of the action of iterates of 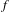$f$ on the cohomology of 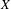$X$ . When 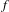$f$ has non-empty indeterminacy set, these quantities can be very difficult to determine. We study rational maps 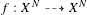$f:X^{N}{\dashrightarrow}X^{N}$ , where 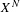$X^{N}$ is isomorphic to the Deligne–Mumford compactification 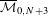$\overline{{\mathcal{M}}}_{0,N+3}$ . We exploit the stratified structure of 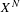$X^{N}$ to provide new examples of rational maps, in arbitrary dimension, for which the action on cohomology behaves functorially under iteration. From this, all dynamical degrees can be readily computed (given enough book-keeping and computing time). In this paper, we explicitly compute all of the dynamical degrees for all such maps 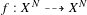$f:X^{N}{\dashrightarrow}X^{N}$ , where 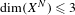$\text{dim}(X^{N})\leq 3$ and the first dynamical degrees for the mappings where 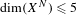$\text{dim}(X^{N})\leq 5$ . These examples naturally arise in the setting of Thurston’s topological characterization of rational maps.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 8 , December 2016 , pp. 2538 - 2579
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amerik, E.. A computation of invariants of a rational self-map. Ann. Fac. Sci. Toulouse Math. (6) 18(3) (2009), 445–457.Google Scholar
Bedford, E.. The dynamical degrees of a mapping. Proceedings of the International Workshop Future Directions in Difference Equations. Publicacións da Universidade de Vigo, Vigo, Spain, 2011, pp. 3–14.Google Scholar
Bedford, E., Cantat, S. and Kim, K.. Pseudo-automorphisms with no invariant foliation. J. Mod. Dyn. 8(2) (2014), 221–250.Google Scholar
Bedford, E. and Kim, K.. On the degree growth of birational mappings in higher dimension. J. Geom. Anal. 14(4) (2004), 567–596.Google Scholar
Bedford, E. and Kim, K.. Degree growth of matrix inversion: birational maps of symmetric, cyclic matrices. Discrete Contin. Dyn. Syst. 21(4) (2008), 977–1013.Google Scholar
Bedford, E. and Kim, K.. Dynamics of (pseudo) automorphisms of 3-space: Periodicity versus positive entropy. Publ. Mat. 58(1) (2014), 65–119.Google Scholar
Bedford, E. and Truong, T. T.. Degree complexity of birational maps related to matrix inversion. Comm. Math. Phys. 298(2) (2010), 357–368.CrossRefGoogle Scholar
Diller, J., Dujardin, R. and Guedj, V.. Dynamics of meromorphic maps with small topological degree I: From cohomology to currents. Indiana Univ. Math. J. 59(2) (2010), 521–561.Google Scholar
Diller, J. and Favre, C.. Dynamics of bimeromorphic maps of surfaces. Amer. J. Math. 123(6) (2001), 1135–1169.Google Scholar
Dinh, T.-C., Nguyen, V.-A. and Truong, T. T.. Equidistribution for meromorphic maps with dominant topological degree. Indiana Univ. Math. J., to appear, arXiv:1303.5992.Google Scholar
Dinh, T.-C. and Sibony, N.. Regularization of currents and entropy. Ann. Sci. Éc. Norm. Supér. (4) 37(6) (2004), 959–971.Google Scholar
Dinh, T.-C. and Sibony, N.. Une borne supérieure pour l’entropie topologique d’une application rationnelle. Ann. of Math. (2) 161(3) (2005), 1637–1644.CrossRefGoogle Scholar
Dinh, T.-C. and Sibony, N.. Super-potentials of positive closed currents, intersection theory and dynamics. Acta Math. 203(1) (2009), 1–82.Google Scholar
Eisenbud, D. and Harris, J.. The Geometry of Schemes (Graduate Texts in Mathematics, 197) . Springer, New York, 2000.Google Scholar
Favre, C.. Les applications monomiales en deux dimensions. Michigan Math. J. 51(3) (2003), 467–475.Google Scholar
Favre, C. and Wulcan, E.. Degree growth of monomial maps and McMullen’s polytope algebra. Indiana Univ. Math. J. 61(2) (2012), 493–524.Google Scholar
Friedland, S.. Entropy of polynomial and rational maps. Ann. of Math. (2) 133(2) (1991), 359–368.Google Scholar
Fulton, W.. Intersection Theory (Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], 2) . 2nd edn. Springer, Berlin, 1998.CrossRefGoogle Scholar
Görtz, U. and Wedhorn, T.. Algebraic Geometry I (Advanced Lectures in Mathematics) . Vieweg + Teubner, Wiesbaden, 2010, Schemes with examples and exercises.CrossRefGoogle Scholar
Griffiths, P. and Harris, J.. Principles of Algebraic Geometry (Wiley Classics Library) . John Wiley & Sons, New York, 1994, reprint of the 1978 original.Google Scholar
Guedj, V.. Entropie topologique des applications méromorphes. Ergod. Th. & Dynam. Sys. 25(6) (2005), 1847–1855.Google Scholar
Guedj, V.. Ergodic properties of rational mappings with large topological degree. Ann. of Math. (2) 161(3) (2005), 1589–1607.Google Scholar
Hartshorne, R.. Algebraic Geometry (Graduate Texts in Mathematics, 52) . Springer, New York, 1977.Google Scholar
Harvey, W. J. and Lloyd-Philipps, A.. Symmetry and moduli spaces for Riemann surfaces. Quasiconformal Mappings, Riemann Surfaces, and Teichmüller Spaces (Contemporary Mathematics, 575) . American Mathematical Society, 2012, pp. 153–170.Google Scholar
Hasselblatt, B. and Propp, J.. Degree-growth of monomial maps. Ergodic Th. & Dynam. Sys. 27(5) (2007), 1375–1397.Google Scholar
Jonsson, M. and Wulcan, E.. Stabilization of monomial maps. Michigan Math. J. 60(3) (2011), 629–660.Google Scholar
Kapranov, M. M.. Veronese curves and Grothendieck–Knudsen moduli space M 0, n . J. Algebraic Geom. 2(2) (1993), 239–262.Google Scholar
Keel, S.. Intersection theory of moduli space of stable n-pointed curves of genus zero. Trans. Amer. Math. Soc. 330(2) (1992), 545–574.Google Scholar
Knudsen, F.. The projectivity of the moduli space of stable curves II: The stacks M g, n . Math. Scand. 52 (1983), 161–199.Google Scholar
Knudsen, F. and Mumford, D.. The projectivity of the moduli space of stable curves I: Preliminaries on ‘det’ and ‘div’. Math. Scand. 39 (1976), 19–55.Google Scholar
Koch, S.. Teichmüller theory and critically finite endomorphisms. Adv. Math. 248 (2013), 573–617.Google Scholar
Lin, J.-L.. Pulling back cohomology classes and dynamical degrees of monomial maps. Bull. Soc. Math. France 140(4) (2013,2012), 533–549.Google Scholar
Lin, J.-L.. On degree growth and stabilization of three-dimensional monomial maps. Michigan Math. J. 62(3) (2013), 567–579.CrossRefGoogle Scholar
Lin, J.-L. and Wulcan, E.. Stabilization of monomial maps in higher codimension. Ann. Inst. Fourier (Grenoble) 64(5) (2014), 2127–2146.Google Scholar
Lloyd-Philipps, A.. Exceptional Weyl groups and complex geometry. PhD Thesis, King’s College London, 2007.Google Scholar
Roeder, R.. The action on cohomology by compositions of rational maps. Math. Res. Lett. 22(2) (2015), 605–632.Google Scholar
Russakovskii, A. and Shiffman, B.. Value distribution for sequences of rational mappings and complex dynamics. Indiana Univ. Math. J 46(3) (1997), 897–932.Google Scholar
Silverman, J.. Dynamical degree, arithmetic entropy, and canonical heights for dominant rational self-maps of projective space. Ergodic Th. & Dynam. Sys. 34(2) (2014), 647–678.Google Scholar
Terada, T.. Quelques propriétés géométriques du domaine de f 1 et le groupe de tresses colorées. Publ. RIMS, Kyoto Univ. 17 (1981), 95–111.Google Scholar