Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T02:35:50.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Commutator criteria for strong mixing

Published online by Cambridge University Press:  21 July 2015

R. TIEDRA DE ALDECOA
R. TIEDRA DE ALDECOA*
Affiliation:
Facultad de Matemáticas, Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, Santiago, Chile email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present new criteria, based on commutator methods, for the strong mixing property of discrete flows 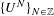$\{U^{N}\}_{N\in \mathbb{Z}}$ and continuous flows 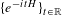$\{e^{-itH}\}_{t\in \mathbb{R}}$ induced by unitary operators 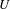$U$ and self-adjoint operators 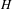$H$ in a Hilbert space 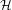${\mathcal{H}}$ . Our approach put into light a general definition for the topological degree of the maps 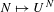$N\mapsto U^{N}$ and 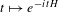$t\mapsto e^{-itH}$ with values in the unitary group of 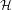${\mathcal{H}}$ . Among other examples, our results apply to skew products of compact Lie groups, time changes of horocycle flows and adjacency operators on graphs.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 1 , February 2017 , pp. 308 - 323
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akhiezer, N. I. and Glazman, I. M.. Theory of Linear Operators in Hilbert Space. Dover Publications, Inc., New York, 1993, Translated from the Russian and with a preface by Merlynd Nestell, Reprint of the 1961 and 1963 translations.Google Scholar
Amrein, W. O., Boutet de Monvel, A. and Georgescu, V.. C 0 -groups, Commutator Methods and Spectral Theory of N-body Hamiltonians (Progress in Mathematics, 135) . Birkhäuser, Basel, 1996.Google Scholar
Anzai, H.. Ergodic skew product transformations on the torus. Osaka J. Math. 3 (1951), 83–99.Google Scholar
Azencott, R. and Parry, W.. Stability of group representations and Haar spectrum. Trans. Amer. Math. Soc. 172 (1972), 317–327.CrossRefGoogle Scholar
Fernández, C., Richard, S. and Tiedra de Aldecoa, R.. Commutator methods for unitary operators. J. Spectr. Theory 3(3) (2013), 271–292.CrossRefGoogle Scholar
Forni, G. and Ulcigrai, C.. Time-changes of horocycle flows. J. Mod. Dyn. 6(2) (2012), 251–273.CrossRefGoogle Scholar
Fra̧czek, K.. Circle extensions of Z d -rotations on the d-dimensional torus. J. Lond. Math. Soc. (2) 61(1) (2000), 139–162.CrossRefGoogle Scholar
Fra̧czek, K.. On cocycles with values in the group SU(2). Monatsh. Math. 131(4) (2000), 279–307.Google Scholar
Fra̧czek, K.. On the degree of cocycles with values in the group SU(2). Israel J. Math. 139 (2004), 293–317.CrossRefGoogle Scholar
Furstenberg, H.. The unique ergodicity of the horocycle flow. Recent Advances in Topological Dynamics (Proc. Conf., Yale Univ., New Haven, Conn., 1972; in honor of Gustav Arnold Hedlund) (Lecture Notes in Mathematics, 318) . Springer, Berlin, 1973, pp. 95–115.Google Scholar
Gabriel, P., Lemańczyk, M. and Liardet, P.. Ensemble d’invariants pour les produits croisés de Anzai. Mém. Soc. Math. Fr. (N.S.) 47 (1991), 1–102.Google Scholar
Grafakos, L.. Classical Fourier Analysis (Graduate Texts in Mathematics, 249) , 2nd edn. Springer, New York, 2008.CrossRefGoogle Scholar
Humphries, P. D.. Change of velocity in dynamical systems. J. Lond. Math. Soc. (2) 7 (1974), 747–757.CrossRefGoogle Scholar
Iwanik, A., Lemańczyk, M. and Rudolph, D.. Absolutely continuous cocycles over irrational rotations. Israel J. Math. 83(1–2) (1993), 73–95.CrossRefGoogle Scholar
Karaliolios, N.. Aspects globaux de la réductibilité des cocycles quasi-périodiques à valeurs dans des groupes de Lie compacts semi-simples. PhD Thesis, Université Pierre et Marie Curie, Paris, 2013. Preprint on http://tel.archives-ouvertes.fr/docs/00/77/79/11/PDF/these.pdf.Google Scholar
Kushnirenko, A. G.. Spectral properties of certain dynamical systems with polynomial dispersal. Moscow Univ. Math. Bull. 29(1) (1974), 82–87.Google Scholar
Măntoiu, M., Richard, S. and Tiedra de Aldecoa, R.. Spectral analysis for adjacency operators on graphs. Ann. Henri Poincaré 8(7) (2007), 1401–1423.CrossRefGoogle Scholar
Măntoiu, M. and Tiedra de Aldecoa, R.. Spectral analysis for convolution operators on locally compact groups. J. Funct. Anal. 253(2) (2007), 675–691.CrossRefGoogle Scholar
Marcus, B.. Ergodic properties of horocycle flows for surfaces of negative curvature. Ann. of Math. (2) 105(1) (1977), 81–105.CrossRefGoogle Scholar
Parry, W.. Topics in Ergodic Theory (Cambridge Tracts in Mathematics, 75) . Cambridge University Press, Cambridge, 1981.Google Scholar
Reed, M. and Simon, B.. Methods of Modern Mathematical Physics, III: Scattering Theory. Academic Press [Harcourt Brace Jovanovich Publishers], New York, 1979, Scattering theory.Google Scholar
Tiedra de Aldecoa, R.. The absolute continuous spectrum of skew products of compact lie groups. Israel J. Math. in press. Preprint, 2013, arXiv:1307.7348.Google Scholar
Tiedra de Aldecoa, R.. Spectral analysis of time changes of horocycle flows. J. Mod. Dyn. 6(2) (2012), 275–285.CrossRefGoogle Scholar
Tiedra de Aldecoa, R.. Commutator methods for the spectral analysis of uniquely ergodic dynamical systems. Ergod. Th. & Dynam. Sys. 35(3) (2014), 944–967.CrossRefGoogle Scholar
Weidmann, J.. Linear Operators in Hilbert Spaces (Graduate Texts in Mathematics, 68) . Springer, New York, 1980, translated from the German by Joseph Szücs.CrossRefGoogle Scholar
Wysokińska, M.. A class of real cocycles over an irrational rotation for which Rokhlin cocycle extensions have Lebesgue component in the spectrum. Topol. Methods Nonlinear Anal. 24(2) (2004), 387–407.CrossRefGoogle Scholar