Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T06:00:39.098Z Has data issue: false hasContentIssue false
  • English
  • Français

Circle maps and 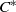${C}^{\ast } $-algebras

Published online by Cambridge University Press:  28 August 2013

THOMAS LUNDSGAARD SCHMIDT  and
KLAUS THOMSEN
THOMAS LUNDSGAARD SCHMIDT
Affiliation:
Institut for Matematik, Aarhus University, Ny Munkegade, 8000 Aarhus C, Denmark email [email protected]@imf.au.dk
KLAUS THOMSEN
Affiliation:
Institut for Matematik, Aarhus University, Ny Munkegade, 8000 Aarhus C, Denmark email [email protected]@imf.au.dk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a construction of 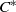${C}^{\ast } $-algebras from continuous piecewise monotone maps on the circle which generalizes the crossed product construction for homeomorphisms and more generally the construction of Renault, Deaconu and Anantharaman-Delaroche for local homeomorphisms. Assuming that the map is surjective and not locally injective we give necessary and sufficient conditions for the simplicity of the 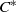${C}^{\ast } $-algebra and show that it is then a Kirchberg algebra. We provide tools for the calculation of the 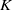$K$-theory groups and turn them into an algorithmic method for Markov maps.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 2 , April 2015 , pp. 546 - 584
Copyright
© Cambridge University Press, 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alsedá, Ll., del Rìo, M. A. and Rodrìguez, J. A.. A splitting theorem for transitive maps. J. Math. Anal. Appl. 232 (1999), 359–375.Google Scholar
Anantharaman-Delaroche, C.. Purely infinite ${C}^{\ast } $-algebras arising from dynamical systems. Bull. Soc. Math. France 125 (1997), 199–225.Google Scholar
Anantharaman-Delaroche, C. and Renault, J.. Amenable Groupoids (Monographies de L’Enseignement Mathmatique, 36). L’Enseignement Mathmatique, Geneva, 2000.Google Scholar
Arzumanian, V. and Renault, J.. Examples of pseudogroups and their $C$-algebras. Operator Algebras and Quantum Field Theory (Rome, 1996). International Press, Cambridge, MA, 1997, pp. 93–104.Google Scholar
Auslander, J. and Katznelson, Y.. Continuous maps of the circle without periodic points. Israel J. Math. 32 (1979), 375–381.Google Scholar
Andersen, K. K. S. and Thomsen, K.. The ${C}^{\ast } $-algebra of an affine map on the 3-torus. Doc. Math. 17 (2012), 531–558.Google Scholar
Coven, E. M. and Mulvey, I.. Transitivity and the centre for maps of the circle. Ergod. Th. & Dynam. Sys. 6 (1986), 1–8.Google Scholar
Deaconu, V.. Groupoids associated with endomorphisms. Trans. Amer. Math. Soc. 347 (1995), 1779–1786.CrossRefGoogle Scholar
Deaconu, V. and Shultz, F.. ${C}^{\ast } $-algebras associated with interval maps. Trans. Amer. Math. Soc. 359 (2007), 1889–1924.CrossRefGoogle Scholar
Katsura, T.. On ${C}^{\ast } $-algebras associated with ${C}^{\ast } $-correspondences. J. Funct. Anal. 217 (2004), 366–401.Google Scholar
Phillips, N. C.. A classification theorem for nuclear purely infinite simple ${C}^{\ast } $-algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
Putnam, I. and Spielberg, J.. The structure of ${C}^{\ast } $-algebras associated with hyperbolic dynamical systems. J. Funct. Anal. 163 (1999), 279–299.CrossRefGoogle Scholar
Raeburn, I. and Williams, D. P.. Morita Equivalence and Continuous-Trace C∗-algebras. American Mathematical Society, Providence, RI, 1998.Google Scholar
Renault, J.. A Groupoid Approach to C∗-algebras (Lecture Notes in Mathematics, 793). Springer, New York, 1980.Google Scholar
Rosenberg, J. and Schochet, C.. The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized $K$-functor. Duke J. Math. 55 (1987), 337–347.CrossRefGoogle Scholar
Shultz, F.. Dimension groups for interval maps II: the transitive case. Ergod. Th. & Dynam. Sys. 27 (2007), 1287–1321.Google Scholar
Sims, A. and Williams, D.. Renault’s equivalence theorem for reduced groupoid ${C}^{\ast } $-algebras. Preprint (2010), arXiv:1002.3093v2.Google Scholar
Spielberg, J.. Groupoids and ${C}^{\ast } $-algebras for categories of paths. Preprint (2011), arXiv:1111.6924v3.Google Scholar
Thomsen, K.. Semi-étale groupoids and applications. Ann. Inst. Fourier 60 (2010), 759–800.Google Scholar
Thomsen, K.. KMS states and conformal measures. Comm. Math. Phys. 316 (2012), 615–640.Google Scholar
Thomsen, K.. The groupoid ${C}^{\ast } $-algebra of a rational map. J. Non-commut. Geom. to appear.Google Scholar
Thomsen, K.. The ${C}^{\ast } $-algebra of the exponential function. Proc. Amer. Math. Soc. to appear.Google Scholar
Thomsen, K.. The homoclinic and heteroclinic ${C}^{\ast } $-algebras of a generalized one-dimensional solenoid. Ergod. Th. & Dynam. Sys. 30 (2010), 263–308.CrossRefGoogle Scholar
Toms, A.. $K$-theoretic rigidity and slow dimension growth. Invent. Math. 183 (2011), 225–244.CrossRefGoogle Scholar
Tu, J.-L.. La conjecture de Baum-Connes pour les feuilletages moyennables. K-theory 17 (1999), 215–264.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1979.Google Scholar
Yokoi, K.. Strong transitivity and graph maps. Bull. Pol. Acad. Math. 53 (2005), 377–388.CrossRefGoogle Scholar