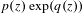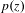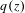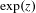Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Cumsille, Patricio
González-Marín, Juan
Honorato, Gerardo
and
Lugo, Diego
2022.
Disconnected Julia set of Halley's method for exponential maps.
Dynamical Systems,
Vol. 37,
Issue. 2,
p.
280.
Lodge, Russell
Mikulich, Yauhen
and
Schleicher, Dierk
2022.
In the Tradition of Thurston II.
p.
421.
Mamayusupov, Khudoyor
Çilingir, Figen
Ruziboev, Marks
Ibragimov, Gafurjan
and
Pansera, Bruno Antonio
2025.
Generating Special Curves for Cubic Polynomials.
Mathematics,
Vol. 13,
Issue. 3,
p.
401.