Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T05:49:03.316Z Has data issue: false hasContentIssue false
  • English
  • Français

A categorical invariant of flow equivalence of shifts

Published online by Cambridge University Press:  30 September 2014

ALFREDO COSTA  and
BENJAMIN STEINBERG
ALFREDO COSTA
Affiliation:
CMUC, Department of Mathematics, University of Coimbra, 3001-501 Coimbra, Portugal email [email protected]
BENJAMIN STEINBERG
Affiliation:
Department of Mathematics, City College of New York, NAC 8/133, Convent Ave at 138th Street, New York, NY 10031, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the Karoubi envelope of a shift—defined as the Karoubi envelope of the syntactic semigroup of the language of blocks of the shift—is, up to natural equivalence of categories, an invariant of flow equivalence. More precisely, we show that the action of the Karoubi envelope on the Krieger cover of the shift is a flow invariant. An analogous result concerning the Fischer cover of a synchronizing shift is also obtained. From these main results, several flow equivalence invariants—some new and some old—are obtained. We also show that the Karoubi envelope is, in a natural sense, the best possible syntactic invariant of flow equivalence of sofic shifts. Another application concerns the classification of Markov–Dyck and Markov–Motzkin shifts: it is shown that, under mild conditions, two graphs define flow equivalent shifts if and only if they are isomorphic. Shifts with property (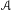$\mathscr{A}$) and their associated semigroups, introduced by Wolfgang Krieger, are interpreted in terms of the Karoubi envelope, yielding a proof of the flow invariance of the associated semigroups in the cases usually considered (a result recently announced by Krieger), and also a proof that property (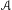$\mathscr{A}$) is decidable for sofic shifts.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 470 - 513
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, C. J. and Hall, T. E.. Inverse semigroups on graphs. Semigroup Forum 11(2) (1975/76), 140–145.CrossRefGoogle Scholar
Bates, T., Eilers, S. and Pask, D.. Reducibility of covers of AFT shifts. Israel J. Math. 185 (2011), 207–234.CrossRefGoogle Scholar
Béal, M. P.. Codage Symbolique. Masson, Paris, 1993.Google Scholar
Béal, M. P., Berstel, J., Eilers, S. and Perrin, D.. Symbolic dynamics. Preprint, 2010, arXiv:1006.1265v3 [cs.FL].Google Scholar
Béal, M. P., Fiorenzi, F. and Perrin, D.. A hierarchy of shift equivalent sofic shifts. Theoret. Comput. Sci. 345 (2005), 190–205.CrossRefGoogle Scholar
Béal, M. P., Fiorenzi, F. and Perrin, D.. The syntactic graph of a sofic shift is invariant under shift equivalence. Int. J. Algebra Comput. 16(3) (2006), 443–460.CrossRefGoogle Scholar
Beauquier, D.. Minimal automaton for a factorial transitive rational language. Theoret. Comput. Sci. 67 (1985), 65–73.CrossRefGoogle Scholar
Blanchard, F. and Hansel, G.. Systèmes codés. Theoret. Comput. Sci. 44 (1986), 17–49.CrossRefGoogle Scholar
Boyle, M.. Flow equivalence of shifts of finite type via positive factorizations. Pacific J. Math. 204(2) (2002), 273–317.CrossRefGoogle Scholar
Boyle, M., Carlsen, T. M. and Eilers, S.. Flow equivalence of sofic shifts (in preparation).Google Scholar
Clifford, A. H. and Preston, G. B.. The Algebraic Theory of Semigroups, Vol. I. American Mathematical Society, Providence, RI, 1961.CrossRefGoogle Scholar
Costa, A.. Conjugacy invariants of subshifts: an approach from profinite semigroup theory. Int. J. Algebra Comput. 16(4) (2006), 629–655.CrossRefGoogle Scholar
Costa, A.. Pseudovarieties defining classes of sofic subshifts closed under taking shift equivalent subshifts. J. Pure Appl. Algebra 209 (2007), 517–530.CrossRefGoogle Scholar
Costa, A.. Semigrupos Profinitos e Dinâmica Simbólica. PhD Thesis, Faculdade de Ciências da Universidade do Porto, 2007.Google Scholar
Costa, A. and Steinberg, B.. The Schützenberger category of a semigroup. Preprint, 2014, arXiv:1408.1615 [math.GR].CrossRefGoogle Scholar
Costa, A. and Steinberg, B.. Profinite groups associated to sofic shifts are free. Proc. Lond. Math. Soc. 102 (2011), 341–369.CrossRefGoogle Scholar
Costa, A. and Steinberg, B.. A categorical invariant of flow equivalence of shifts. Technical Report,arXiv:1304.3487 [math.DS], 2013.Google Scholar
Delgado, M., Linton, S. and Morais, J.. Automata: A GAP package on finite automata. http://www.gap-system.org/Packages/automata.html.Google Scholar
Delgado, M. and Morais, J.. SgpViz: A GAP package to visualize finite semigroups, http://www.gap-system.org/Packages/sgpviz.html, 2008.Google Scholar
Eilenberg, S.. Automata, Languages and Machines, Vol. B. Academic Press, New York, 1976.Google Scholar
Fiebig, D. and Fiebig, U.-R.. Covers for coded systems. Symbolic Dynamics and its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135). American Mathematical Society, Providence, RI, 1992, pp. 139–179.CrossRefGoogle Scholar
Fischer, R.. Sofic systems and graphs. Monatsh. Math. 80 (1975), 179–186.CrossRefGoogle Scholar
Franks, J.. Flow equivalence of subshifts of finite type. Ergod. Th. & Dynam. Sys. 4(1) (1984), 53–66.CrossRefGoogle Scholar
Fujiwara, M. and Osikawa, M.. Sofic systems and flow equivalence. Math. Rep. Kyushu Univ. 16(1) (1987), 17–27.Google Scholar
Funk, J., Lawson, M. V. and Steinberg, B.. Characterizations of Morita equivalent inverse semigroups. J. Pure Appl. Algebra 215(9) (2011), 2262–2279.CrossRefGoogle Scholar
The GAP Group. GAP – Groups, Algorithms, and Programming, Version 4.4, 2006. http://www.gap-system.org.Google Scholar
Hamachi, T., Inoue, K. and Krieger, W.. Subsystems of finite type and semigroup invariants of subshifts. J. Reine Angew. Math. 632 (2009), 37–61.Google Scholar
Hamachi, T. and Krieger, W.. A construction of subshifts and a class of semigroups. Preprint, 2013, arXiv:1303.4158v1 [math.DS].Google Scholar
Hamachi, T. and Krieger, W.. On certain subshifts and their associated monoids. Preprint, 2013, arXiv:1202.5207v2 [math.DS].Google Scholar
Huang, D.. Automorphisms of Bowen–Franks groups of shifts of finite type. Ergod. Th. & Dynam. Sys. 21 (2001), 1113–1137.CrossRefGoogle Scholar
Johansen, R.. On flow equivalence of sofic shifts. PhD Thesis, University of Copenhagen, 2011.Google Scholar
Jones, D. G. and Lawson, M.. Graph inverse semigroups: their characterization and completion. J. Algebra 409 (2014), 444–473.CrossRefGoogle Scholar
Jonoska, N.. Sofic systems with synchronizing representations. Theoret. Comput. Sci. 158 (1996), 81–115.CrossRefGoogle Scholar
Jonoska, N.. A conjugacy invariant for reducible sofic shifts and its semigroup characterizations. Israel J. Math. 106 (1998), 221–249.CrossRefGoogle Scholar
Kim, K. H. and Roush, F. W.. An algorithm for sofic shift equivalence. Ergod. Th. & Dynam. Sys. 10 (1990), 381–393.CrossRefGoogle Scholar
Kim, K. H. and Roush, F. W.. Williams conjecture is false for reducible subshifts. J. Amer. Math. Soc. 5 (1992), 213–215.Google Scholar
Kim, K. H. and Roush, F. W.. The Williams conjecture is false for irreducible subshifts. Ann. of Math. (2) 149 (1999), 545–558.CrossRefGoogle Scholar
Krieger, W.. On the uniqueness of the equilibrium state. Math. Systems Theory 8(2) (1974/1975), 97–104.CrossRefGoogle Scholar
Krieger, W.. On sofic systems I. Israel J. Math. 48 (1984), 305–330.CrossRefGoogle Scholar
Krieger, W.. On a syntactically defined invariant of symbolic dynamics. Ergod. Th. & Dynam. Sys. 20 (2000), 501–516.CrossRefGoogle Scholar
Krieger, W.. On subshifts and semigroups. Bull. Lond. Math. Soc. 38(4) (2006), 617–624.CrossRefGoogle Scholar
Krieger, W.. On subshift presentations. Preprint, 2012, arXiv:1209.2578v1 [math.DS].Google Scholar
Krieger, W. and Matsumoto, K.. Zeta functions and topological entropy of the Markov-Dyck shifts. Münster J. Math. 4 (2011), 171–184.Google Scholar
Lallement, G.. Semigroups and Combinatorial Applications. Wiley, New York, 1979.Google Scholar
Lawson, M. V.. Morita equivalence of semigroups with local units. J. Pure Appl. Algebra 215(4) (2011), 455–470.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
MacLane, S.. Categories for the Working Mathematician (Graduate Texts in Mathematics, 5), 2nd edn. Springer, New York, 1998.Google Scholar
Margolis, S. and Steinberg, B.. Quivers of monoids with basic algebras. Compos. Math. 148(5) (2012), 1516–1560.CrossRefGoogle Scholar
Matsumoto, K.. Bowen–Franks groups as an invariant for flow equivalence of subshifts. Ergod. Th. & Dynam. Sys. 21(6) (2001), 1831–1842.CrossRefGoogle Scholar
Matsumoto, K.. A certain synchronizing property of subshifts and flow equivalence. Israel J. Math. 196 (2013), 235–272.CrossRefGoogle Scholar
Nasu, M.. Topological conjugacy for sofic systems. Ergod. Th. & Dynam. Sys. 6 (1986), 265–280.CrossRefGoogle Scholar
Parry, B. and Sullivan, D.. A topological invariant of flows on 1-dimensional spaces. Topology 14(4) (1975), 297–299.CrossRefGoogle Scholar
Parry, W. and Tuncel, S.. Classification Problems in Ergodic Theory (London Mathematical Society Lecture Note Series, 67). Cambridge University Press, Cambridge, 1982.CrossRefGoogle Scholar
Paterson, A. L. T.. Groupoids, Inverse Semigroups, and Their Operator Algebras (Progress in Mathematics, 170). Birkhäuser, Boston, 1999.CrossRefGoogle Scholar
Paterson, A. L. T.. Graph inverse semigroups, groupoids and their C ∗ -algebras. J. Operator Theory 48(3, suppl.) (2002), 645–662.Google Scholar
Petrich, M.. Inverse Semigroups. Wiley, New York, 1984.Google Scholar
Pin, J.-E.. Varieties of formal languages. Foundations of Computer Science. Plenum, New York, 1986.Google Scholar
Rhodes, J. and Steinberg, B.. The q-Theory of Finite Semigroups (Springer Monographs in Mathematics). Springer, New York, 2009.CrossRefGoogle Scholar
Steinberg, B.. Strong Morita equivalence of inverse semigroups. Houston J. Math. 37(3) (2011), 895–927.Google Scholar
Talwar, S.. Morita equivalence for semigroups. J. Aust. Math. Soc. Ser. A 59(1) (1995), 81–111.CrossRefGoogle Scholar
Tilson, B.. Categories as algebra: an essential ingredient in the theory of monoids. J. Pure Appl. Algebra 48 (1987), 83–198.CrossRefGoogle Scholar