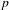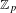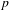Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jeong, Sangtae
2018.
Bernoulli maps on Z in the expansions of van der Put and Mahler.
Journal of Number Theory,
Vol. 193,
Issue. ,
p.
235.
Furno, Joanna
2019.
Natural extensions for p-adic β-shifts and other scaling maps.
Indagationes Mathematicae,
Vol. 30,
Issue. 6,
p.
1099.
Hbaib, M.
Guidara, S.
and
Zouari, S.
2024.
On the conjecture of Erdős, Joò and Komornik for p-adic numbers.
Research in Number Theory,
Vol. 10,
Issue. 3,