Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-29T03:02:34.145Z Has data issue: false hasContentIssue false
  • English
  • Français

Basins of measures on inverse limit spaces for the induced homeomorphism

Published online by Cambridge University Press:  13 October 2009

JUDY KENNEDY ,
BRIAN E. RAINES  and
DAVID R. STOCKMAN
JUDY KENNEDY
Affiliation:
Department of Mathematics, Lamar University, Beaumont, TX 77710, USA (email: [email protected])
BRIAN E. RAINES
Affiliation:
Department of Mathematics, Baylor University, Waco, TX 76798, USA (email: [email protected])
DAVID R. STOCKMAN
Affiliation:
Department of Economics, University of Delaware, Newark, DE 19716, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let f:X→X be continuous and onto, where X is a compact metric space. Let 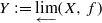be the inverse limit and F:Y →Y the induced homeomorphism. Suppose that μ is an f-invariant measure, and let m be the measure induced on Y by (μ,μ,…). We show that B is a basin of μ if and only if π−11(B) is a basin of m. From this it follows that if μ is an SRB measure for f on X, then the induced measure m on Y is an inverse-limit SRB measure for F. Conversely, if m is an inverse-limit SRB measure for F on Y, then the induced measure μ on X is an SRB measure for f.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 4 , August 2010 , pp. 1119 - 1130
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Grandmont, J.-M.. On endogenous competitive business cycles. Econometrica 53 (1985), 995–1045.CrossRefGoogle Scholar
[2]Ingram, W. T. and Mahavier, W. S.. Interesting dynamics and inverse limits in a family of one-dimensional maps. Amer. Math. Monthly 111(3) (2004), 198–215.CrossRefGoogle Scholar
[3]Kennedy, J. A. and Stockman, D. R.. Chaotic equilibria in models with backward dynamics. J. Econom. Dynam. Control 32 (2008), 939–955.Google Scholar
[4]Kennedy, J. A., Stockman, D. R. and Yorke, J. A.. Inverse limits and an implicitly defined difference equation from economics. Topology Appl. 154 (2007), 2533–2552.CrossRefGoogle Scholar
[5]Kennedy, J. A., Stockman, D. R. and Yorke, J. A.. The inverse limits approach to models with chaos. J. Math. Econom. 44 (2008), 423–444.CrossRefGoogle Scholar
[6]Li, S.. Dynamical properties of the shift maps on the inverse limit spaces. Ergod. Th. Dynam. Sys. 12(1) (1992), 95–108.CrossRefGoogle Scholar
[7]Lucas, R. E. and Stokey, N. L.. Money and interest in a cash-in-advance economy. Econometrica 55 (1987), 491–513.CrossRefGoogle Scholar
[8]Medio, A. and Raines, B.. Inverse limit spaces arising from problems in economics. Topology Appl. 153 (2006), 3439–3449.CrossRefGoogle Scholar
[9]Medio, A. and Raines, B.. Backward dynamics in economics. The inverse limit approach. J. Econom. Dynam. Control 31 (2007), 1633–1671.CrossRefGoogle Scholar
[10]Michener, R. and Ravikumar, B.. Chaotic dynamics in a cash-in-advance economy. J. Econom. Dynam. Control 22 (1998), 1117–1137.CrossRefGoogle Scholar
[11]Parthasarathy, K. R.. Probability Measures on Metric Spaces. American Mathematical Society, Providence, RI, 2005. Reprint of the 1967 original.Google Scholar
[12]Rudin, W.. Principles of Mathematical Analysis, 3rd edn(International Series in Pure and Applied Mathematics). McGraw-Hill, New York, 1976.Google Scholar
[13]Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1982.CrossRefGoogle Scholar