Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:28:41.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Automorphisms of the shift: Lyapunov exponents, entropy, and the dimension representation

Part of: Topological dynamics

Published online by Cambridge University Press:  25 March 2019

SCOTT SCHMIEDING
SCOTT SCHMIEDING*
Affiliation:
Northwestern University, Mathematics Department, 2033 Sheridan Road, Evanston, IL 60208, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 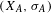$(X_{A},\unicode[STIX]{x1D70E}_{A})$ be a shift of finite type and 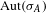$\text{Aut}(\unicode[STIX]{x1D70E}_{A})$ its corresponding automorphism group. Associated to 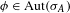$\unicode[STIX]{x1D719}\in \text{Aut}(\unicode[STIX]{x1D70E}_{A})$ are certain Lyapunov exponents 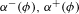$\unicode[STIX]{x1D6FC}^{-}(\unicode[STIX]{x1D719}),\unicode[STIX]{x1D6FC}^{+}(\unicode[STIX]{x1D719})$, which describe asymptotic behavior of the sequence of coding ranges of 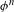$\unicode[STIX]{x1D719}^{n}$. We give lower bounds on 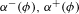$\unicode[STIX]{x1D6FC}^{-}(\unicode[STIX]{x1D719}),\unicode[STIX]{x1D6FC}^{+}(\unicode[STIX]{x1D719})$ in terms of the spectral radius of the corresponding action of 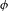$\unicode[STIX]{x1D719}$ on the dimension group associated to 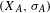$(X_{A},\unicode[STIX]{x1D70E}_{A})$. We also give lower bounds on the topological entropy 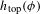$h_{\text{top}}(\unicode[STIX]{x1D719})$ in terms of a distinguished part of the spectrum of the action of $\unicode[STIX]{x1D719}$ on the dimension group, but show that, in general, 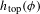$h_{\text{top}}(\unicode[STIX]{x1D719})$ is not bounded below by the logarithm of the spectral radius of the action of $\unicode[STIX]{x1D719}$ on the dimension group.

Keywords

automorphismLyapunov exponentsentropyshift of finite type

MSC classification

Primary: 37B10: Symbolic dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2552 - 2570
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boyle, M.. Constraints on the degree of a sofic homomorphism and the induced multiplication of measures on unstable sets. Israel J. Math. 53(1) (1986), 52–68.Google Scholar
Boyle, M. and Handelman, D.. The spectra of nonnegative matrices via symbolic dynamics. Ann. of Math. (2) 133(2) (1991), 249–316.Google Scholar
Boyle, M. and Krieger, W.. Periodic points and automorphisms of the shift. Trans. Amer. Math. Soc. 302(1) (1987), 125–149.Google Scholar
Boyle, M. and Lind, D.. Expansive subdynamics. Trans. Amer. Math. Soc. 349(1) (1997), 55–102.Google Scholar
Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.Google Scholar
Boyle, M., Marcus, B. and Trow, P.. Resolving maps and the dimension group for shifts of finite type. Mem. Amer. Math. Soc. 70(377) (1987), vi+146.Google Scholar
Coven, E. M. and Paul, M. E.. Endomorphisms of irreducible subshifts of finite type. Math. Systems Theory 8(2) (1974/75), 167–175.Google Scholar
Cyr, V., Franks, J. and Kra, B.. The spacetime of a shift automorphism. Trans. Amer. Math. Soc. 371(1) (2019), 461–488.Google Scholar
Cyr, V., Franks, J., Kra, B. and Petite, S.. Distortion and the automorphism group of a shift. Preprint, 2016,arXiv:1611.05913.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma 3 (2015), e5, 27 pp.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a minimal shift of stretched exponential growth. J. Mod. Dyn. 10 (2016), 483–495.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of subquadratic growth. Proc. Amer. Math. Soc. 144(2) (2016), 613–621.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys. 36(1) (2016), 64–95.Google Scholar
Fiebig, U.-R.. Periodic points and finite group actions on shifts of finite type. Ergod. Th. & Dynam. Sys. 13(3) (1993), 485–514.Google Scholar
Guillon, P. and Salo, V.. Distortion in one-head machines and cellular automata. Cellular Automata and Discrete Complex Systems. Springer, Cham, 2017, pp. 120–138.Google Scholar
Katok, A. B.. The Entropy Conjecture. Izdat. ‘Mir’, Moscow, 1977, pp. 181–203; Engl. transl. Trans. Amer. Math. Soc. (Series 2), 133 (1986), 91–107.Google Scholar
Killough, D. B. and Putnam, I. F.. Ring and module structures on dimension groups associated with a shift of finite type. Ergod. Th. & Dynam. Sys. 32(4) (2012), 1370–1399.Google Scholar
Kim, K. H., Ormes, N. S. and Roush, F. W.. The spectra of nonnegative integer matrices via formal power series. J. Amer. Math. Soc. 13(4) (2000), 773–806.Google Scholar
Lax, P. D.. Functional Analysis (Pure and Applied Mathematics). Wiley-Interscience [John Wiley & Sons], New York, 2002.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Lubotzky, A., Mozes, S. and Raghunathan, M. S.. The word and Riemannian metrics on lattices of semisimple groups. Publ. Math. Inst. Hautes Études Sci. 91(2001) (2000), 5–53.Google Scholar
Nasu, M.. The degrees of onesided resolvingness and the limits of onesided resolving directions for endomorphisms and automorphisms of the shift. Preprint, 2010.Google Scholar
Nasu, M.. Textile systems for endomorphisms and automorphisms of the shift. Mem. Amer. Math. Soc. 114(546) (1995), viii+215.Google Scholar
Pacifico, M. J. and Vieitez, J. L.. Lyapunov exponents for expansive homeomorphisms. Preprint, 2017,arXiv:1704.05284.Google Scholar
Putnam, I. F.. A homology theory for Smale spaces. Mem. Amer. Math. Soc. 232(1094) (2014), viii+122.Google Scholar
Shereshevsky, M. A.. Lyapunov exponents for one-dimensional cellular automata. J. Nonlinear Sci. 2(1) (1992), 1–8.Google Scholar
Shub, M.. Dynamical systems, filtrations and entropy. Bull. Amer. Math. Soc. 80 (1974), 27–41.Google Scholar
Tisseur, P.. Cellular automata and Lyapunov exponents. Nonlinearity 13(5) (2000), 1547–1560.Google Scholar