Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T04:16:17.847Z Has data issue: false hasContentIssue false
  • English
  • Français

The automorphism group of a shift of slow growth is amenable

Part of: Topological dynamics Abstract harmonic analysis Discrete mathematics in relation to computer science

Published online by Cambridge University Press:  11 December 2018

VAN CYR  and
BRYNA KRA
VAN CYR
Affiliation:
Bucknell University, Lewisburg, PA 17837, USA email [email protected]
BRYNA KRA
Affiliation:
Northwestern University, Evanston, IL 60208, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose 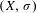$(X,\unicode[STIX]{x1D70E})$ is a subshift, 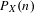$P_{X}(n)$ is the word complexity function of 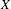$X$, and 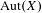$\text{Aut}(X)$ is the group of automorphisms of 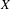$X$. We show that if 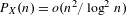$P_{X}(n)=o(n^{2}/\log ^{2}n)$, then 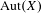$\text{Aut}(X)$ is amenable (as a countable, discrete group). We further show that if 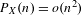$P_{X}(n)=o(n^{2})$, then $\text{Aut}(X)$ can never contain a non-abelian free monoid (and, in particular, can never contain a non-abelian free subgroup). This is in contrast to recent examples, due to Salo and Schraudner, of subshifts with quadratic complexity that do contain such a monoid.

Keywords

subshiftautomorphismblock complexityamenable

MSC classification

Primary: 37B50: Multi-dimensional shifts of finite type, tiling dynamics
Secondary: 43A07: Means on groups, semigroups, etc.; amenable groups 68R15: Combinatorics on words
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 7 , July 2020 , pp. 1788 - 1804
Copyright
© Cambridge University Press, 2018

References

Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.Google Scholar
Cyr, V., Franks, J., Petite, S. and Kra, B.. Distortion and the automorphism group of a shift. J. Mod. Dyn., to appear.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of subquadratic growth. Proc. Amer. Math. Soc. 144(2) (2016), 613–621.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a shift of linear growth: beyond transitivity. Forum Math. Sigma 3 (2015), e5.Google Scholar
Cyr, V. and Kra, B.. The automorphism group of a minimal shift of stretched exponential growth. J. Mod. Dyn. 10 (2016), 483–495.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of low complexity subshifts. Ergod. Th. & Dynam. Sys. 36(1) (2016), 64–95.Google Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. On automorphism groups of Toeplitz subshifts. Discrete Anal. (2017), Paper No. 11, 19 pp.Google Scholar
Hedlund, G. A.. Endomorphisms and automorphisms of the shift dynamical system. Math. Systems Theory. 3 (1969), 320–375.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.Google Scholar
Quas, A. and Zamboni, L.. Periodicity and local complexity. Theoret. Comput. Sci. 319 (2004), 229–240.Google Scholar
Salo, V. and Schraudner, M.. Automorphism groups of subshifts through group extensions. Preprint.Google Scholar