Article contents
Asymptotically holomorphic methods for infinitely renormalizable 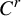 $C^r$ unimodal maps
$C^r$ unimodal maps
Published online by Cambridge University Press: 29 November 2022
Abstract
The purpose of this paper is to initiate a theory concerning the dynamics of asymptotically holomorphic polynomial-like maps. Our maps arise naturally as deep renormalizations of asymptotically holomorphic extensions of 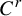 $C^r$ (
$C^r$ (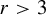 $r>3$) unimodal maps that are infinitely renormalizable of bounded type. Here we prove a version of the Fatou–Julia–Sullivan theorem and a topological straightening theorem in this setting. In particular, these maps do not have wandering domains and their Julia sets are locally connected.
$r>3$) unimodal maps that are infinitely renormalizable of bounded type. Here we prove a version of the Fatou–Julia–Sullivan theorem and a topological straightening theorem in this setting. In particular, these maps do not have wandering domains and their Julia sets are locally connected.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by



