Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T20:58:37.871Z Has data issue: false hasContentIssue false
  • English
  • Français

Arithmeticity of discrete subgroups

Part of: Discontinuous groups and automorphic forms Lie groups Other groups of matrices

Published online by Cambridge University Press:  28 September 2020

YVES BENOIST
YVES BENOIST*
Affiliation:
CNRS, Université Paris-Sud, France (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The topic of this course is the discrete subgroups of semisimple Lie groups. We discuss a criterion that ensures that such a subgroup is arithmetic. This criterion is a joint work with Sébastien Miquel, which extends previous work of Selberg and Hee Oh and solves an old conjecture of Margulis. We focus on concrete examples like the group 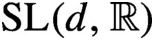$\mathrm {SL}(d,{\mathbb {R}})$ and we explain how classical tools and new techniques enter the proof: the Auslander projection theorem, the Bruhat decomposition, the Mahler compactness criterion, the Borel density theorem, the Borel–Harish-Chandra finiteness theorem, the Howe–Moore mixing theorem, the Dani–Margulis recurrence theorem, the Raghunathan–Venkataramana finite-index subgroup theorem and so on.

Keywords

semisimple grouparithmetic groupparabolic grouplatticethin group

MSC classification

Primary: 22E40: Discrete subgroups of Lie groups
Secondary: 11F06: Structure of modular groups and generalizations; arithmetic groups 20H05: Unimodular groups, congruence subgroups
Type
Survey Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 9 , September 2021 , pp. 2561 - 2590
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Beardon, A. F.. The Geometry of Discrete Groups (Graduate Texts in Mathematics, 91). Springer, Berlin, 1983.CrossRefGoogle Scholar
Benoist, Y.. Five Lectures on Lattices in Semisimple Lie Groups (Séminaires Congrés, 18). Société Mathématique de France, Paris, 2009, pp. 117–176.Google Scholar
Benoist, Y. and Miquel, S.. Arithmeticity of discrete subgroups containing horospherical lattices. Duke Math. J. 169 (2020), 1485–1539 .CrossRefGoogle Scholar
Benoist, Y. and Oh, H.. Discrete subgroups of $\textsf{SL}(3,\mathbb{R})$ generated by triangular matrices. Int. Math. Res. Not. 149 (2010), 619–634.Google Scholar
Benoist, Y. and Oh, H.. Discreteness criterion for subgroups of products of $\textsf{SL}(2)$ . Transform. Groups 15 (2010), 503–515.CrossRefGoogle Scholar
Borel, A.. Arithmetic properties of linear algebraic groups. Proc. Int. Congr. Math., 1962 (1963), 10–22.Google Scholar
Borel, A.. Introduction aux groupes arithmétiques. Hermann, Paris, 1969.Google Scholar
Borel, A. and Harish-Chandra. Arithmetic subgroups of algebraic groups. Ann. Math. 75 (1962), 485–535.CrossRefGoogle Scholar
Borel, A. and Tits, J.. Groupes réductifs. Publ. Math. Inst. Hautes Études Sci. 27 (1965), 55–151.CrossRefGoogle Scholar
Chatterji, I. and Venkataramana, T.. Discrete linear groups containing arithmetic groups. Preprint, 2009, arXiv/0905.1813, 1–24.Google Scholar
Dani, S.. On invariant measures, minimal sets and a lemma of Margulis. Invent. Math. 51 (1979), 239–260.CrossRefGoogle Scholar
MacLane, S.. Homology (Graduate Texts in Mathematics, 114). Springer, Berlin, 1967.Google Scholar
Margulis, G.. Arithmetic properties of discrete subgroups. Russian Math. Surveys 29 (1974), 107–156.CrossRefGoogle Scholar
Margulis, G.. Discrete Subgroups of Semisimple Lie Groups. Springer, Berlin, 1991.CrossRefGoogle Scholar
Margulis, G. and Tomanov, G.. Invariant measures for actions of unipotent groups over local fields. Invent. Math. 116 (1994), 347–392.CrossRefGoogle Scholar
Miquel, S.. Arithméticité de sous-groupes de produits de groupes de rang un. J. Inst. Math. Jussieu 18 (2017), 1–24.Google Scholar
Morris, D.. Introduction to Arithmetic Groups. Deductive Press, Lethbridge, 2015.Google Scholar
Oh, H.. Arithmetic properties of some Zariski dense discrete subgroups. Lie Groups and Ergodic Theory (Studia Mathematica). Tata Institute of Fundamental Research, Mumbai, 1998, pp. 151–165.Google Scholar
Oh, H.. Discrete subgroups generated by lattices in opposite horospherical subgroups. J. Algebra 203 (1998), 621–676.CrossRefGoogle Scholar
Oh, H.. On discrete subgroups containing a lattice in a horospherical subgroup. Israel J. Math. 110 (1999), 333–340.CrossRefGoogle Scholar
Raghunathan, M.. Discrete Subgroups of Lie Groups. Springer, Berlin, 1972.CrossRefGoogle Scholar
Raghunathan, M.. On the congruence subgroup problem. Publ. Math. Inst. Hautes Études Sci. 46 (1976), 107–161.CrossRefGoogle Scholar
Raghunathan, M. S.. A note on generators for arithmetic subgroups of algebraic groups. Pacific J. Math. 152(2) (1992), 365–373.CrossRefGoogle Scholar
Ratner, M.. Raghunathan’s topological conjecture and distributions of unipotent flows. Duke Math. J. 63 (1991), 235–280.CrossRefGoogle Scholar
Selberg, A.. Notes on discrete subgroups of motions of products of upper half planes. Unpublished.Google Scholar
Tits, J.. Systèmes générateurs de groupes de congruence. C. R. Math. Acad. Sci. Paris 283 (1976), 693–695.Google Scholar
Vaserstein, L.. The structure of classical arithmetic subgroups of rank greater than one. Sb. Math. 20 (1973), 465–492.CrossRefGoogle Scholar
Venkataramana, T.. On systems of generators of arithmetic subgroups of higher rank groups. Pacific J. Math. 166 (1994), 193–212.CrossRefGoogle Scholar
Zimmer, R.. Ergodic Theory and Semisimple Groups. Birkhäuser, Basel, 1984.CrossRefGoogle Scholar