Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T12:52:56.679Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation properties of 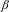$\unicode[STIX]{x1D6FD}$-expansions II

Published online by Cambridge University Press:  14 February 2017

SIMON BAKER
SIMON BAKER*
Affiliation:
Department of Mathematics and Statistics, Whiteknights, PO Box 220, Reading RG6 6AX, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 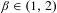$\unicode[STIX]{x1D6FD}\in (1,2)$ be a real number. For a function 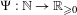$\unicode[STIX]{x1D6F9}:\mathbb{N}\rightarrow \mathbb{R}_{\geq 0}$, define 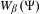$W_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6F9})$ to be the set of 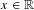$x\in \mathbb{R}$ such that for infinitely many 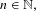$n\in \mathbb{N},$ there exists a sequence 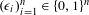$(\unicode[STIX]{x1D716}_{i})_{i=1}^{n}\in \{0,1\}^{n}$ satisfying 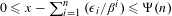$0\leq x-\sum _{i=1}^{n}(\unicode[STIX]{x1D716}_{i}/\unicode[STIX]{x1D6FD}^{i})\leq \unicode[STIX]{x1D6F9}(n)$. In Baker [Approximation properties of 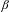$\unicode[STIX]{x1D6FD}$-expansions. Acta Arith. 168 (2015), 269–287], the author conjectured that for Lebesgue almost every 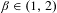$\unicode[STIX]{x1D6FD}\in (1,2)$, the condition 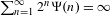$\sum _{n=1}^{\infty }2^{n}\unicode[STIX]{x1D6F9}(n)=\infty$ implies that 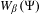$W_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6F9})$ is of full Lebesgue measure within 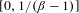$[0,1/(\unicode[STIX]{x1D6FD}-1)]$. In this paper we make a significant step towards proving this conjecture. We prove that given a sequence of positive real numbers 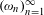$(\unicode[STIX]{x1D714}_{n})_{n=1}^{\infty }$ satisfying 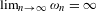$\lim _{n\rightarrow \infty }\unicode[STIX]{x1D714}_{n}=\infty$, for Lebesgue almost every 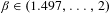$\unicode[STIX]{x1D6FD}\in (1.497,\ldots ,2)$, the set 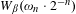$W_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D714}_{n}\cdot 2^{-n})$ is of full Lebesgue measure within 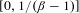$[0,1/(\unicode[STIX]{x1D6FD}-1)]$. We also study the case where 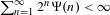$\sum _{n=1}^{\infty }2^{n}\unicode[STIX]{x1D6F9}(n)<\infty$ in which the set 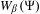$W_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6F9})$ has Lebesgue measure zero. Applying the mass transference principle developed by Beresnevich and Velani in [A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) (2006), 971–992], we obtain some results on the Hausdorff dimension and the Hausdorff measure of 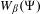$W_{\unicode[STIX]{x1D6FD}}(\unicode[STIX]{x1D6F9})$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1627 - 1641
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baker, S.. Approximation properties of 𝛽-expansions. Acta Arith. 168 (2015), 269–287.Google Scholar
Benjamini, I. and Solomyak, B.. Spacings and pair correlations for finite Bernoulli convolutions. Nonlinearity 22(2) (2009), 381–393.Google Scholar
Beresnevich, V. and Velani, S.. A mass transference principle and the Duffin–Schaeffer conjecture for Hausdorff measures. Ann. of Math. (2) 164(3) (2006), 971–992.Google Scholar
Dajani, K., Komornik, V., Loreti, P. and de Vries, M.. Optimal expansions in non-integer bases. Proc. Amer. Math. Soc. 140(2) (2012), 437–447.Google Scholar
Duffin, R. J. and Schaeffer, A. C.. Khintchine’s problem in metric Diophantine approximation. Duke Math. J. 8 (1941), 243–255.Google Scholar
Durand, A.. Sets with large intersection and ubiquity. Math. Proc. Cambridge Philos. Soc. 144(1) (2008), 119–144.Google Scholar
Falconer, K.. Sets with large intersection properties. J. Lond. Math. Soc. (2) 49(2) (1994), 267–280.Google Scholar
Garsia, A.. Arithmetic properties of Bernoulli convolutions. Trans. Amer. Math. Soc. 102 (1962), 409–432.Google Scholar
Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.CrossRefGoogle Scholar
Hochman, M.. On self-similar sets with overlaps and inverse theorems for entropy. Ann. of Math. (2) 180(2) (2014), 773–822.Google Scholar
Khintchine, A.. Einige Sätze über Kettenbruche, mit Anwendungen auf die Theorie der Diophantischen Approximationen. Math. Ann. 92 (1924), 115–125.Google Scholar
Komornik, V.. Expansions in non-integer bases. Integers 11B (2011), Paper No A9, 30 pp. 11A63.Google Scholar
Komornik, V. and Loreti, P.. Unique developments in non-integer bases. Amer. Math. Monthly 105(7) (1998), 636–639.CrossRefGoogle Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hung. 11 (1960), 401–416.CrossRefGoogle Scholar
Persson, T. and Reeve, H.. On the Diophantine properties of 𝜆-expansions. Mathematika 59(1) (2013), 65–86.Google Scholar
Persson, T. and Reeve, H.. A Frostman type lemma for sets with large intersections, and an application to Diophantine approximation. Proc. Edinb. Math. Soc. (2) 58(02) (2015), 521–542.Google Scholar
Rényi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hung. 8 (1957), 477–493.CrossRefGoogle Scholar
Shmerkin, P.. On the exceptional set for absolute continuity of Bernoulli convolutions. Geom. Funct. Anal. 24(3) (2014), 946–958.CrossRefGoogle Scholar
Sidorov, N.. Almost every number has a continuum of 𝛽-expansions. Amer. Math. Monthly 110(9) (2003), 838–842.Google Scholar
Sidorov, N.. Arithmetic dynamics. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 145–189.Google Scholar
Solomyak, B.. On the random series ∑ ±𝜆 n (an Erdős problem). Ann. of Math. (2) 142(3) (1995), 611–625.CrossRefGoogle Scholar