Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T04:01:42.758Z Has data issue: false hasContentIssue false
  • English
  • Français

Approximation by Brownian motion for Gibbs measures and flows under a function

Published online by Cambridge University Press:  19 September 2008

Manfred Denker  and
Walter Philipp
Manfred Denker
Affiliation:
Institut für Mathematische Stochastik, Universität Göttingen, Lotzestr. 13 D-3400 Gottingen, West Germany;
Walter Philipp
Affiliation:
Department of Mathematics, University of Illinois, Urbana, IL 61801, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

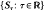Let denote a flow built under a Hölder-continuous function l over the base (Σ, μ) where Σ is a topological Markov chain and μ some (ψ-mining) Gibbs measure. For a certain class of functions f with finite 2 + δ-moments it is shown that there exists a Brownian motion B(t) with respect to μ and σ2 > 0 such that μ-a.e.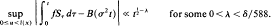

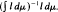for some 0 < λ < 5δ/588. One can also approximate in the same way by a Brownian motion B*(t) with respect to the probability . From this, the central limit theorem, the weak invariance principle, the law of the iterated logarithm and related probabilistic results follow immediately. In particular, the result of Ratner ([6]) is extended.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 4 , Issue 4 , December 1984 , pp. 541 - 552
Copyright
Copyright © Cambridge University Press 1984

References

REFERENCES

[1]Billingsley, P.. Convergence of Probability Measures. J. Wiley: New York, 1968.Google Scholar
[2]Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms. Lecture Notes in Math. 470. Springer: Berlin-Heidelberg-New York, 1975.CrossRefGoogle Scholar
[3]Doob, J. L.. Stochastic Processes. J. Wiley: New York, 1953.Google Scholar
[4]Ibragimov, I. A.. Some limit theorems for stationary processes. Theor. Probability Appl. 7 (1962) 349–382.CrossRefGoogle Scholar
[5]Philipp, W. & Stout, W.. Almost sure invariance principles for partial sums of weakly dependent random variables. Mem. Amer. Math. Soc. 161 (1975).Google Scholar
[6]Ratner, M.. The central limit theorem for geodesic flows on n-dimensional manifolds of negative curvature. Israel J. Math. 16 (1973), 181–197.CrossRefGoogle Scholar
[7]Renyi, A.. Wahrscheinlichkeitsrechnung. Deutscher Verlag Wissensch.: Berlin, 1962.Google Scholar
[8]Ruelle, D., Statistical mechanics of a one-dimensional lattice gas. Commun. Math. Phys. 9 (1968), 267–278.CrossRefGoogle Scholar
[9]Serfling, R. J., Moment inequalities for the maximum cumulative sum. Ann. Math. Stat. 41 (1970), 1227–1234CrossRefGoogle Scholar
[10]Sinai, Y. G., Gibbs measures in ergodic theory. Uspeki Mat. Nauk (4) 27 (1972), 21–63.Google Scholar