Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T03:28:20.835Z Has data issue: false hasContentIssue false
  • English
  • Français

An answer to Furstenberg’s problem on topological disjointness

Part of: Connections with other structures, applications Topological dynamics

Published online by Cambridge University Press:  10 April 2019

WEN HUANG ,
SONG SHAO  and
XIANGDONG YE
WEN HUANG
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences and Department of Mathematics, University of Science and Technology of China, Hefei, Anhui, 230026, PR China email [email protected], [email protected], [email protected]
SONG SHAO
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences and Department of Mathematics, University of Science and Technology of China, Hefei, Anhui, 230026, PR China email [email protected], [email protected], [email protected]
XIANGDONG YE
Affiliation:
Wu Wen-Tsun Key Laboratory of Mathematics, USTC, Chinese Academy of Sciences and Department of Mathematics, University of Science and Technology of China, Hefei, Anhui, 230026, PR China email [email protected], [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we give an answer to Furstenberg’s problem on topological disjointness. Namely, we show that a transitive system 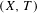$(X,T)$ is disjoint from all minimal systems if and only if 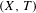$(X,T)$ is weakly mixing and there is some countable dense subset 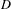$D$ of 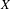$X$ such that for any minimal system 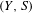$(Y,S)$, any point 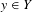$y\in Y$ and any open neighbourhood $V$ of $y$, and for any non-empty open subset 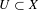$U\subset X$, there is 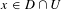$x\in D\cap U$ such that 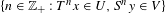$\{n\in \mathbb{Z}_{+}:T^{n}x\in U,S^{n}y\in V\}$ is syndetic. Some characterization for the general case is also given. By way of application we show that if a transitive system 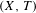$(X,T)$ is disjoint from all minimal systems, then so are 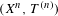$(X^{n},T^{(n)})$ and 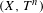$(X,T^{n})$ for any 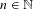$n\in \mathbb{N}$. It turns out that a transitive system 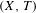$(X,T)$ is disjoint from all minimal systems if and only if the hyperspace system 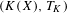$(K(X),T_{K})$ is disjoint from all minimal systems.

Keywords

topological dynamicsjoiningdisjointweak mixingcentral set

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 54H20: Topological dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2467 - 2481
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E. and Kolyada, S.. Li-Yorke sensitivity. Nonlinearity 16 (2003), 1421–1433.Google Scholar
Dai, X.. On disjointness and weak-mixing of ${\mathcal{F}}$-flows with discrete abelian phase groups. Preprint, 2017.Google Scholar
Dong, P., Shao, S. and Ye, X.. Product recurrent properties, disjointness and weak disjointness. Israel J. Math. 188 (2012), 463–507.Google Scholar
Feng, D. and Huang, W.. Variational principles for topological entropies of subsets. J. Funct. Anal. 263(8) (2012), 2228–2254.Google Scholar
Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory. Int. J. Math. Comput. Theory 1 (1967), 1–49.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 1981.Google Scholar
Glasner, E.. Ergodic Theory via Joinings (Mathematical Surveys and Monographs, 101). American Mathematical Society, Providence, RI, 2003.Google Scholar
Glasner, E. and Weiss, B.. On the disjointness property of groups and a conjecture of Furstenberg. Preprint, 2018, arXiv:1807.08493.Google Scholar
Gottschalk, W. and Hedlund, G.. Topological Dynamics (Colloquium Publications, 36). American Mathematical Society, Providence, RI, 1955.Google Scholar
Huang, W. and Ye, X.. An explicit scattering, non-weakly mixing example and weak disjointness. Nonlinearity 15 (2002), 1–14.Google Scholar
Huang, W. and Ye, X.. Dynamical systems disjoint from any minimal system. Trans. Amer. Math. Soc. 357(2) (2005), 669–694.Google Scholar
Li, J., Yan, K. and Ye, X.. Recurrence properties and disjointness on the induced spaces. Discrete Contin. Dyn. Syst. 35 (2015), 1059–1073.Google Scholar
Li, J., Oprocha, P., Ye, X. and Zhang, R.. When are all closed subsets recurrent? Ergod. Th. & Dynam. Sys. 37(7) (2017), 2223–2254.Google Scholar
Oprocha, P.. Weak mixing and product recurrence. Ann. Inst. Fourier (Grenoble) 60(4) (2010), 1233–1257.Google Scholar
Oprocha, P.. Double minimality, entropy and disjointness with all minimal systems. Discrete Contin. Dyn. Syst. 39 (2019), 263–275.Google Scholar
Yu, T.. Dynamical systems disjoint from any minimal system under group actions. Difference Equations, Discrete Dynamical Systems and Applications, 181–195 (Springer Proceedings in Mathematics and Statistics, 150). Springer, Cham, 2015.Google Scholar