Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T16:00:17.976Z Has data issue: false hasContentIssue false
  • English
  • Français

Amenable purely infinite actions on the non-compact Cantor set

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  20 November 2018

GÁBOR ELEK
GÁBOR ELEK*
Affiliation:
Department of Mathematics And Statistics, Fylde College, Lancaster University, Lancaster, LA1 4YF, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that any countable non-amenable group 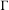$\unicode[STIX]{x1D6E4}$ admits a free, minimal, amenable, purely infinite action on the non-compact Cantor set. This answers a question of Kellerhals, Monod and Rørdam [Non-supramenable groups acting on locally compact spaces. Doc. Math.18 (2013), 1597–1626].

Keywords

Minimal actionsnon-compact Cantor settopological amenabilitypurely infinite actions

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 6 , June 2020 , pp. 1619 - 1633
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anantharaman-Delaroche, C.. Amenability and exactness for dynamical systems and their C ∗ -algebras. Trans. Amer. Math. Soc. 354 (2002), 4153–4178.Google Scholar
Benjamini, I. and Schramm, O.. Every graph with a positive Cheeger constant contains a tree with a positive Cheeger constant. Geom. Funct. Anal. 7(3) (1997), 403–419.Google Scholar
Danilenko, A. I.. On simplicity concepts for ergodic actions. J. Anal. Math. 102 (2007), 77–117.Google Scholar
Danilenko, A. I.. Rank-one actions, their $(C,F)$-models and constructions with bounded parameters. Preprint, 2016, arXiv:1610.09851.Google Scholar
Deuber, W. A., Simonovits, M. and Sós, V. T.. A note on paradoxical metric spaces. Studia Sci. Math. Hungar. 30 (1995), 17–23.Google Scholar
Drutu, C. and Kapovich, M.. Geometric Group Theory (American Mathematical Society Colloquium Publication, 63). American Mathematical Society, Providence, RI, 2018. With an appendix by Bogdan Nica.Google Scholar
Elek, G.. Uniformly recurrent subgroups and simple C ∗ -algebras. J. Funct. Anal. 274(6) (2018), 1657–1689.Google Scholar
Glasner, E. and Weiss, B.. Uniformly recurrent subgroups. Recent Trends in Ergodic Theory and Dynamical Systems (Contemporary Mathematics, 631). American Mathematical Society, Providence, RI, 2015, pp. 63–75.Google Scholar
Guentner, E., Willett, R. and Yu, G.. Dynamical asymptotic dimension: relation to dynamics, topology, coarse geometry and C ∗ -algebras. Math. Ann. 367(1–2) (2017), 785–829.Google Scholar
Kellerhals, J., Monod, N. and Rørdam, M.. Non-supramenable groups acting on locally compact spaces. Doc. Math. 18 (2013), 1597–1626.Google Scholar
Matui, H. and Rørdam, M.. Universal properties of group actions on locally compact spaces. J. Funct. Anal. 268(12) (2015), 3601–3648.Google Scholar
Rørdam, M. and Sierakowski, A.. Purely infinite C ∗ -algebras arising from crossed products. Ergod. Th. & Dynam. Sys. 32(1) (2012), 273–293.Google Scholar