Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-12-05T02:42:28.788Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic torsion, zeta function and Dirichlet series for graph links in homology 3-spheres

Published online by Cambridge University Press:  19 September 2008

András Némethi
András Némethi
Affiliation:
Department of Mathematics, The Ohio State University, Columbus, Ohio, 43210-1174, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we define the algebraic torsion τ associated with an 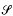-constructible sheaf ℱ on a topological space X and a ring homomorphism π1(X) → Z (with an acyclicity condition). If (X, 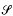) has a fiber structure over S1, then τ is equal to the zeta function of the monodromy acting on the hypercohomology of the fiber. If X is the complement of a link 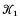in a homology 3-sphere and 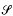is given by a link 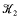such that 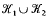admits a fiberable splice diagram, then this zeta function has a product decomposition (corresponding to the Jaco-Shalen-Johansson decomposition). This can be interpreted as a ‘Lefschetz type formula’ for a dynamical system suitably chosen.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 13 , Issue 1 , March 1993 , pp. 131 - 142
Copyright
Copyright © Cambridge University Press 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]A'Campo, N.. La fonction zêta d'une monodromie. Comment. Math. Helv. 50 (1975), 233–248.CrossRefGoogle Scholar
[2]Cheeger, J.. Analytic torsion and the heat equation. Ann. Math. 109 (1979), 259–322.CrossRefGoogle Scholar
[3]Eisenbud, D. & Neumann, W.. Three-dimensional link theory and invariants of plane curve singularities. Ann. Math. Studies 110, Princeton University Press, 1985.Google Scholar
[4]Franks, J. M.. Knots, links, and symbolic dynamics. Ann. Math. 113 (1981), 529–552.CrossRefGoogle Scholar
[5]Fried, D.. Homological identities for closed orbits. Inv. Math. 71 (1983), 419–442.CrossRefGoogle Scholar
[6]Fried, D.. Lefschetz formulas for flows. In The Lefschetz Centennial Conference, Part III. Contemp. Math. 58 (1987) 19–69.CrossRefGoogle Scholar
[7]Fried, D.. Counting circles. Dynamical Systems. Springer Lecture Notes in Mathematics 1342, Springer, Berlin, 1988, 196–215.Google Scholar
[8]Fried, D.. Analytic torsion and closed geodesies on hyperbolic manifolds. Invent. Math. 84 (1986), 523–540.CrossRefGoogle Scholar
[9]Fuller, F. B.. An index of fixed point type for periodic orbits. Amer. J. Math. 87 (1965), 473–480.CrossRefGoogle Scholar
[10]Godement, R.. Topologie Alg∈brique et Th∈orie des Faisceaux, Hermann, Paris, 1958.Google Scholar
[11]Goresky, M.. Triangulation of stratified objects. Proc. Amer. Math. Soc. 72 (1988), 193–200.CrossRefGoogle Scholar
[12]Tr´ng, Lê Dũng. The geometry of the monodromy theorem. Studies in Mathematics, No. 8. Springer, Berlin, 1978, 157–173.Google Scholar
[13]Tr∈ng, Lê Dũng. Some remarks on relative monodromy. Nordic Summer School/NAVF, 1976, 397–403.CrossRefGoogle Scholar
[14]Milnor, J.. Whitehead torsion, Bull. Amer. Math. Soc. 72 (1966), 358–426.CrossRefGoogle Scholar
[15]Milnor, J.. Infinite cyclic coverings. Conf. on the Topology of Manifolds. Prindle, Weber and Schmidt, Boston, MA, 1968, 115–133.Google Scholar
[16]Moscovici, H. & Stanton, R. J.. R-torsion and zeta functions for locally symmetric manifolds. Inv. Math. 105 (1991), 185–216.CrossRefGoogle Scholar
[17]Müller, W.. Analytic torsion and R-torsion of Riemannian manifolds. Adv. Math. 28 (1978), 233–305.CrossRefGoogle Scholar
[18]Némethi, A.. The Milnor fiber and the zeta function of the singularities of type ƒ = P(h, g). Comp. Math. 79 (1991), 63–97.Google Scholar
[19]Némethi, A.. Global Sebastiani-Thom theorem for polynomial maps. J. Math. Soc. Japan 43 (1991), 213–218.Google Scholar
[20]Némethi, A.. Generalised local and global Sebastiani-Thom type theorems. Comp. Math. 80 (1991), 1–14.Google Scholar
[21]Némethi, A.. The zeta function of singularities, J. Alg. Geom. to appear.Google Scholar
[22]Pollicott, M.. The differential zeta function for Axiom A attractors. Ann. Math. 131 (1990), 331–354.CrossRefGoogle Scholar