Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T16:16:09.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Algebraic geometry of the center-focus problem for Abel differential equations

Published online by Cambridge University Press:  06 November 2014

M. BRISKIN ,
F. PAKOVICH  and
Y. YOMDIN
M. BRISKIN
Affiliation:
Jerusalem College of Engineering, Ramat Bet Hakerem, P.O.B. 3566, Jerusalem 91035, Israel email [email protected]
F. PAKOVICH
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel email [email protected]
Y. YOMDIN
Affiliation:
Department of Mathematics, The Weizmann Institute of Science, Rehovot 76100, Israel email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Abel differential equation 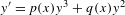$y^{\prime }=p(x)y^{3}+q(x)y^{2}$ with polynomial coefficients 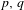$p,q$ is said to have a center on $[a,b]$ if all its solutions, with the initial value 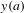$y(a)$ small enough, satisfy the condition 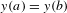$y(a)=y(b)$. The problem of giving conditions on $(p,q,a,b)$ implying a center for the Abel equation is analogous to the classical Poincaré center-focus problem for plane vector fields. Center conditions are provided by an infinite system of ‘center equations’. During the last two decades, important new information on these equations has been obtained via a detailed analysis of two related structures: composition algebra and moment equations (first-order approximation of the center ones). Recently, one of the basic open questions in this direction—the ‘polynomial moments problem’—has been completely settled in Pakovich and Muzychuk [Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3)99(3) (2009), 633–657] and Pakovich [Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math.149 (2013), 705–728]. In this paper, we present a progress in the following two main directions: first, we translate the results of Pakovich and Muzychuk [Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3)99(3) (2009), 633–657] and Pakovich [Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math.149 (2013), 705–728] into the language of algebraic geometry of the center equations. Applying these new tools, we show that the center conditions can be described in terms of composition algebra, up to a ‘small’ correction. In particular, we significantly extend the results of Briskin, Roytvarf and Yomdin [Center conditions at infinity for Abel differential equations. Ann. of Math. (2)172(1) (2010), 437–483]. Second, applying these tools in combination with explicit computations, we start in this paper the study of the ‘second Melnikov coefficients’ (second-order approximation of the center equations), showing that in many cases vanishing of the moments and of these coefficients is sufficient in order to completely characterize centers.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 3 , May 2016 , pp. 714 - 744
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alvarez, A., Bravo, J. L. and Christopher, C.. On the trigonometric moment problem. Ergod. Th. & Dynam. Sys. 34(1) (2014), 1–20.Google Scholar
Alwash, M. A. M.. On the composition conjectures. Electron. J. Differential Equations 2003(69) (2003), 1–4.Google Scholar
Alwash, M. A. M.. The composition conjecture for Abel equation. Expo. Math. 27 (2009), 241–250.Google Scholar
Alwash, M. A. M.. Polynomial differential equations with piecewise linear coefficients. Differ. Equ. Dyn. Syst. 19(3) (2011), 267–281.Google Scholar
Alwash, M. A. M.. Composition conditions for two-dimensional polynomial systems. Differ. Equ. Appl. 5(1) (2013), 1–12.Google Scholar
Alwash, M. A. M. and Lloyd, N. G.. Non-autonomous equations related to polynomial two-dimensional systems. Proc. Roy. Soc. Edinburgh 105A (1987), 129–152.Google Scholar
Blinov, M., Briskin, M. and Yomdin, Y.. Local center conditions for the Abel equation and cyclicity of its zero solution. Complex Analysis and Dynamical Systems II (Contemporary Mathematics, 382). American Mathematical Society, Providence, RI, 2005, pp. 65–82.Google Scholar
Briskin, M., Francoise, J.-P. and Yomdin, Y.. Center conditions, compositions of polynomials and moments on algebraic curve. Ergod. Th. & Dynam. Sys. 19(5) (1999), 1201–1220.Google Scholar
Briskin, M., Pakovich, F. and Yomdin, Y.. Parametric center-focus problem for Abel equation. Qual. Theory Dyn. Syst. to appear.Google Scholar
Briskin, M., Roytvarf, N. and Yomdin, Y.. Center conditions at infinity for Abel differential equations. Ann. of Math. (2) 172(1) (2010), 437–483.Google Scholar
Brudnyi, A.. On the center problem for ordinary differential equations. Amer. J. Math. 128(2) (2006), 419–451.Google Scholar
Brudnyi, A.. Center problem for ODEs with coefficients generating the group of rectangular paths. C. R. Math. Acad. Sci. Soc. R. Can. 31(2) (2009), 33–44.Google Scholar
Brudnyi, A. and Yomdin, Y.. Tree composition condition and moments vanishing. Nonlinearity 23(7) (2010), 1651–1673.CrossRefGoogle Scholar
Christopher, C. and Li, Ch.. Limit Cycles of Differential Equations (Advanced Courses in Mathematics. CRM Barcelona). Birkhäuser, Basel, 2007, viii+171.Google Scholar
Cima, A., Gasull, A. and Manosas, F.. Centers for trigonometric Abel equations. Qual. Theory Dyn. Syst. 11(1) (2012), 19–37.CrossRefGoogle Scholar
Cima, A., Gasull, A. and Manosas, F.. A simple solution of some composition conjectures for Abel equations. J. Math. Anal. Appl. 398(2) (2013), 477–486.Google Scholar
Cima, A., Gasull, A. and Manosas, F.. An explicit bound of the number of vanishing double moments forcing composition. J. Differential Equations 255(3) (2013), 339–350.Google Scholar
Cohen, S. D.. The group of translations and positive rational powers is free. Quart. J. Math. Oxford Ser. (2) 46(181) (1995), 21–93.CrossRefGoogle Scholar
Engstrom, H.. Polynomial substitutions. Amer. J. Math. 63 (1941), 249–255.Google Scholar
Giat, Sh., Shelah, Y., Shikelman, C. and Yomdin, Y.. Algebraic geometry of Abel differential equation. Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 108(1) (2014), 193–210.CrossRefGoogle Scholar
Giné, J., Grau, M. and Llibre, J.. Universal centers and composition conditions. Proc. Lond. Math. Soc. (3) 106(3) (2013), 481–507.Google Scholar
Giné, J., Grau, M. and Santallusia, X.. Composition conditions in the trigonometric Abel equation. J. Appl. Anal. Comput. 3(2) (2013), 133–144.Google Scholar
Giné, J., Grau, M. and Santallusia, X.. Universal centers in the cubic trigonometric Abel equation. Electron. J. Qual. Theory Differ. Equ.(1) (2014), No. 1, 7pp.Google Scholar
Golubitski, V. and Guillemin, V.. Stable Mappings and their Singularities (Graduate Texts in Mathematics, 14). Springer, Berlin, 1973.CrossRefGoogle Scholar
Il’yashenko, Yu.. Centennial history of Hilbert’s 16th problem. Bull. Amer. Math. Soc. (N.S.) 39(3) (2002), 301–354.Google Scholar
Levandovskyy, V., Pfister, G. and Romanovski, V.. Evaluating cyclicity of cubic systems with algorithms of computational algebra. Comm. Pure Appl. Anal. 11(5) (2012), 2023–2035.Google Scholar
Llibre, J. and Yang, J.. A classical family of polynomial Abel differential equations satisfying the composition conjecture. Preprint, 2006.Google Scholar
Muzychuk, M. and Pakovich, F.. Jordan–Hölder theorem for imprimitivity systems and maximal decompositions of rational functions. Proc. Lond. Math. Soc. (3) 102(3) (2011), 1–24.Google Scholar
Nakai, I. and Yanai, K.. Relations of formal diffeomorphisms and the center problem. Mosc. Math. J. 10(2) (2010), 415–468.Google Scholar
Pakovich, F.. A counterexample to the ‘composition conjecture’. Proc. Amer. Math. Soc. 130(12) (2002), 3747–3749.Google Scholar
Pakovich, F.. On polynomials orthogonal to all powers of a given polynomial on a segment. Bull. Sci. Math. 129(9) (2005), 749–774.Google Scholar
Pakovich, F.. Prime and composite Laurent polynomials. Bull. Sci. Math. 133 (2009), 693–732.CrossRefGoogle Scholar
Pakovich, F.. Generalized ‘second Ritt theorem’ and explicit solution of the polynomial moment problem. Compositio Math. 149 (2013), 705–728.CrossRefGoogle Scholar
Pakovich, F.. On rational functions orthogonal to all powers of a given rational function on a curve. Mosc. Math. J. 13(4) (2013), 693–731.Google Scholar
Pakovich, F. and Muzychuk, M.. Solution of the polynomial moment problem. Proc. Lond. Math. Soc. (3) 99(3) (2009), 633–657.Google Scholar
Pakovich, F., Pech, C. and Zvonkin, A.. Laurent polynomial moment problem: a case study. Contemp. Math. 532 (2010), 177–194.CrossRefGoogle Scholar
Pakovich, F., Roytvarf, N. and Yomdin, Y.. Cauchy type integrals of algebraic functions. Israel J. Math. 144 (2004), 221–291.Google Scholar
Ritt, J.. Prime and composite polynomials. Trans. Amer. Math. Soc. 23(1) (1922), 51–66.Google Scholar